Tính diện tích, thể tích của hình lăng trụ đứng tam giác, tứ giác

Nối tiếp mạch kiến thức đang có, trong bài viết này chúng ta sẽ cùng nhau tìm hiểu về cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đứng tam giác và lưng trụ đứng tứ giác nha các bạn.

Thật ra chỉ cần biết công thức tính của hình lăng trụ đứng là các bạn đã có thể áp dụng được cho hình lăng trụ đứng tam giác, tứ giác, hình hộp chữ nhật và hình lập phương rồi.

Tuy nhiên, vì công thức tính của hình lăng trụ đứng quá chung chung, không thuận tiện sử dụng nên mới cần đến công thức tính toán riêng cho từng hình cụ thể. Okay, giờ chúng ta sẽ đi đến phần nội dung chính của bài viết này.

#1. Tính diện tích và thể tích của hình lăng trụ đứng tam giác

Định nghĩa: Hình lăng trụ đứng tam giác hình lăng trụ có có các cạnh bên vuông góc với đáy. Hay nói cách khác thì đây là hình có hai đáy là 2 tam giác và mặt bên là các hình chữ nhật.

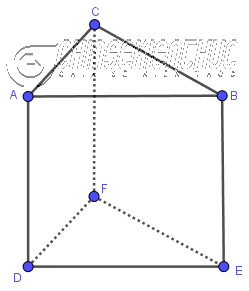
Như các bạn có thể thấy ở hình bên dưới: Hình lăng trụ đứng tam giác là hình lăng trụ đứng có hai mặt đáy là hai hình tam giác và ba mặt bên là ba hình chữ nhật.

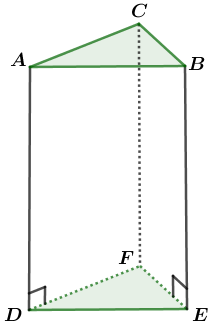
Hình lăng trụ đứng tam giác ABC.DEF có …

• A, B, C, D, E, F là sáu đỉnh
• ACFD, CBEF, BEDA là ba mặt bên, ba mặt bên này là ba hình chữ nhật
• AD, CF, BE là ba cạnh bên, ba cạnh bên này bằng nhau và song song với nhau
• ABC, DEF là hai mặt đáy, hai mặt đáy này song song với nhau
• AD là chiều cao

Diện tích xung quanh của hình lăng trụ đứng tam giác sẽ bằng tích của tổng độ dài ba cạnh đáy và chiều cao

Diện tích toàn phần của hình lăng trụ đứng tam giác sẽ bằng tổng của diện tích xung quanh và diện tích hai tam giác đáy

Thể tích của hình lăng trụ đứng tam giác sẽ bằng tích của diện tích tam giác đáy và chiều cao

Ví dụ 1: Cho hình lăng trụ đứng tam giác ABC.DEF có AC=2 cm, CB=3 cm, BE=3.5 cm, ED=4 cm

Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đứng tam giác.

Lời Giải:

$S_{xq}=(2+3+4) \times 3.5=\frac{63}{2}~cm^2$

Muốn tính được diện tích toàn phần của hình lăng trụ đứng tam giác ABC.DEF chúng ta cần tính được diện tích của tam giác ABC hoặc DEF trước

Ở đây chúng ta nên sử dụng công thức Heron vì đã biết độ dài ba cạnh của tam giác đáy

$S_{ABC}=\sqrt{4.5(4.5-2)(4.5-3)(4.5-4)}=\frac{3\sqrt{15}}{4}\approx 2.9~cm^2$

$S_{tp}=\frac{63}{2}+2 \times \frac{3\sqrt{15}}{4}=\frac{63+3\sqrt{15}}{2}\approx 37.3~cm^2$

$V_{ABC.DEF}=\frac{3\sqrt{15}}{4}\times 3.5=\frac{21\sqrt{15}}{8}\approx 10.2~cm^3$

Vậy diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đứng tam giác đã cho lần lượt gần bằng $31.5~cm^2, 37.3~cm^2, 10.2~cm^3$

#2. Tính diện tích và thể tích của lăng trụ đứng tứ giác

Định nghĩa: Hình lăng trụ đứng tứ giác hình lăng trụ có có các cạnh bên vuông góc với đáy. Hay nói cách khác thì đây là hình có hai đáy là 2 tứ giác và mặt bên là các hình chữ nhật.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

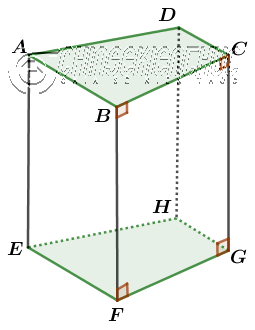
Như các bạn có thể thấy ở hình bên dưới: Hình lăng trụ đứng tứ giác là hình lăng trụ đứng có hai mặt đáy là hai hình tứ giác và bốn mặt bên là bốn hình chữ nhật.

Hình lăng trụ đứng tứ giác ABCD.EFGH có …

• A, B, C, D, E, F, G, H là tám đỉnh
• ADHE, DCGH, CGFB, BFEA là bốn mặt bên, bốn mặt bên này là bốn hình chữ nhật
• AE, DH, CG, BF là bốn cạnh bên, bốn cạnh bên này bằng nhau và song song với nhau
• ABCD, EFGH là hai mặt đáy, hai mặt đáy này song song với nhau
• AE là chiều cao

Diện tích xung quanh của hình lăng trụ đứng tứ giác sẽ bằng tích của tổng độ dài bốn cạnh đáy và chiều cao

Diện tích toàn phần của hình lăng trụ đứng tứ giác sẽ bằng tổng của diện tích xung quanh và diện tích hai tứ giác đáy

Thể tích của hình lăng trụ đứng tứ giác sẽ bằng tích của diện tích tứ giác đáy và chiều cao

Ví dụ 2: Tính diện tích xung quanh của lăng trụ đứng tứ giác (hình thang) với các kích thước như Hình 1

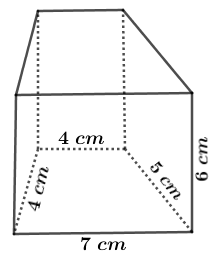
Lời Giải:

Diện tích xung quanh của lăng trụ đứng tứ giác đã cho bằng $(4+4+5+7).6=120~cm^2$

Ví dụ 3: Tính thể tích của lăng trụ đứng tứ giác (hình thang) với các kích thước như Hình 2

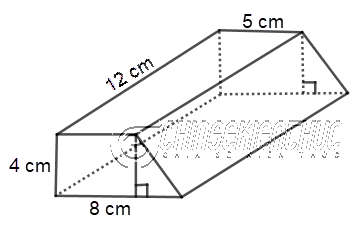
Lời Giải:

Diện tích tứ giác đáy của hình lăng trụ đứng tứ giác đã cho bằng $\frac{1}{2}.(5+8).4=26~cm^2$

=> Thể tích của hình lăng trụ đứng tứ giác đã cho bằng $26.12=312~cm^3$

#3. Công thức tính cho hình lăng trụ đứng bất kỳ

Dưới đây là công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của một hình lăng trụ đứng có đáy là một đa giác bất kì (tam giác, tứ giác, ngũ giác, …)

• Diện tích xung quanh của hình lăng trụ đứng sẽ bằng tích của chu vi đáy, chiều cao $S_{xq}=C_{d}.h$
• Diện tích toàn phần của hình lăng trụ đứng sẽ bằng tổng của diện tích xung quanh, diện tích hai đáy $S_{tp}=S_{xq}+2.S_{d}$
• Thể tích của hình lăng trụ đứng sẽ bằng tích của diện tích đáy, chiều cao $V=S_{d}.h$

#4. Lời kết

Nếu các bạn để ý sẽ thấy, tên của lăng trụ đứng sẽ phụ thuộc vào tên của đa giác đáy, chẳng hạn lăng trụ đứng có đáy là tam giác được gọi là lăng trụ đứng tam giác, lăng trụ đứng có đáy là tứ giác được gọi là lăng trụ đứng tứ giác, …

Có vô số đa giác nên sẽ có vô số lăng trụ đứng, ở đây mình chỉ chọn ra lăng trụ đứng tam giác và lăng trụ đứng tứ giác là vì chúng rất thường gặp trong Toán học cũng như trong cuộc sống.

Cột mốc ngã ba biên giới, tấm lịch để bàn, gàu xúc của xe xúc, hộp đèn, lều trại, … đều có hình dạng của một lăng trụ đứng tam giác, tứ giác…

Okay, như vậy kiến thức cần nắm vững trong bài viết này là:

Biết cách tính diện tích xung quanh của hình lăng trụ đứng tam giác, tứ giác… Biết cách tính diện tích toàn phần của hình lăng trụ đứng tam giác, tứ giác… và biết cách tính thể tích của hình lăng trụ đứng tam giác, tứ giác….

Vậy nhé các bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !

Đọc thêm:

• Cách tính diện tích và thể tích của hình trụ (có ví dụ)
• Cách tính diện tích mặt cầu và thể tích hình cầu (có ví dụ)
• Cách tính thể tích tứ diện trong không gian (công thức & casio)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com