Cách tìm tọa độ trực tâm của tam giác

Ngoài các điểm đặc biệt của tam giác mà chúng ta đã tìm hiểu trong những bài viết trước (như trọng tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp, … ) thì trực tâm cũng đặc biệt không kém !

Vâng, và trong bài viết ngày hôm nay chúng ta sẽ cùng nhau ôn lại cách tìm tọa độ trực tâm của một tam giác bất kỳ..

Đây là công việc đầu tiên cần làm trước khi nghiên cứu các tính chất của trực tâm, vẽ trực tâm, … Okay, ngay bây giờ chúng ta hãy cùng nhau tìm hiểu các bạn nhé …

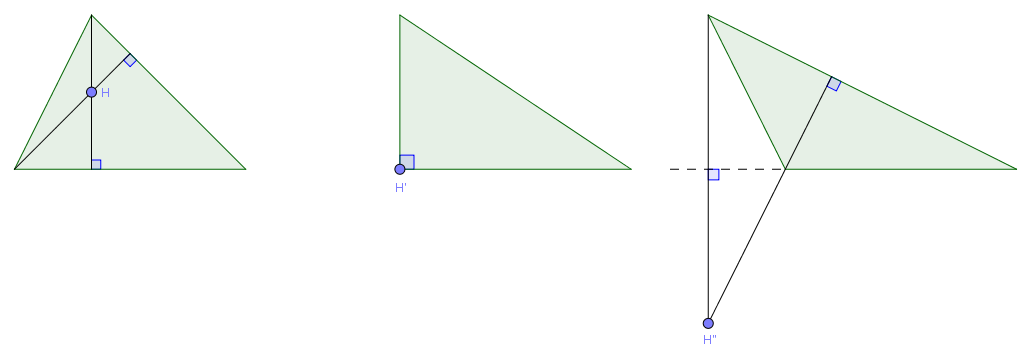
#1. Trực tâm của tam giác là gì?

Định nghĩa: Trực tâm của tam giác là giao điểm của ba đường cao, tam giác nào cũng chỉ có đúng một trực tâm.

Trực tâm không nhất thiết phải nằm bên trong tam giác, cụ thể thì:

• Trực tâm nằm trong tam giác, nếu tam giác đó là tam giác nhọn.
• Trực tâm nằm ngay đỉnh (góc vuông), nếu tam giác đó là tam giác vuông.
• Trực tâm nằm ngoài tam giác, nếu tam giác đó là tam giác tù.

#2. Các bước tìm trực tâm của tam giác

Theo định nghĩa bên trên thì chúng ta chỉ cần viết được 2 phương trình đường cao và tìm được giao điểm là xem như xong.

#3. Bài tập ví dụ về tìm trực tâm của tam giác

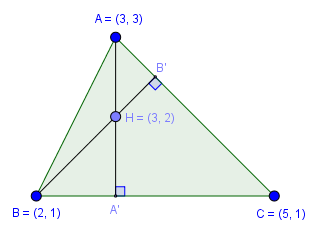
Ví dụ 1. Cho tam giác $ABC$ có $A(3, 3), B(2, 1), C(5, 1)$, tìm tọa độ trực tâm $H$ của tam giác $ABC$

Dễ thấy, phương trình đường cao $(AA’): x-3=0$

Dễ thấy phương trình đường cao $(BB’): x-y-1=0$

Giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x-3=0 \\ x-y-1=0\end{array}\right.$ thu nghiệm là $(3 ,2)$

Vậy tọa độ trực tâm $H$ của tam giác $ABC$ là $(3, 2)$

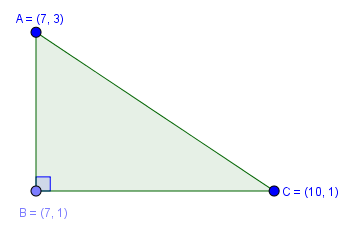
Ví dụ 2. Cho tam giác $ABC$ có $A(7, 3), B(7, 1), C(10, 1)$, tìm tọa độ trực tâm $H$ của tam giác $ABC$

Cách 1. Dựa vào giao điểm của hai đường cao

Dễ thấy phương trình đường cao $(AA’): x-7=0$

Dễ thấy phương trình đường cao $(BB’): y-1=0$

Giả hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x-7=0 \\ y-1=0 \end{array}\right.$ được nghiệm là $(7, 1)$

Vậy tọa độ trực tâm $H \equiv B$ của tam giác $ABC$ là $(7, 1)$

Cách 2. Dựa vào tính chất của trực tâm trong tam giác vuông

Vẽ hệ tọa độ $(Oxy)$ rồi vẽ tam giác $ABC$ lên giấy, quan sát hình vẽ ta dự đoán tam giác $ABC$ vuông tại $B$

Nếu dự đoán trên là đúng thì $B$ chính là trực tâm của tam giác $ABC$

Thật vậy …

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

$\overrightarrow{AB}\cdot\overrightarrow{AC}=(0,- 2)\cdot(3, -2)=0.3+(-2)(-2)=4\neq0$

$\overrightarrow{BA}\cdot\overrightarrow{BC}=(0, 2)\cdot(3, 0)=0.3+2.0=0$

Suy ra tam giác $ABC$ vuông tại $B$

Vậy tọa độ trực tâm $H \equiv B$ của tam giác $ABC$ là $(7, 1)$

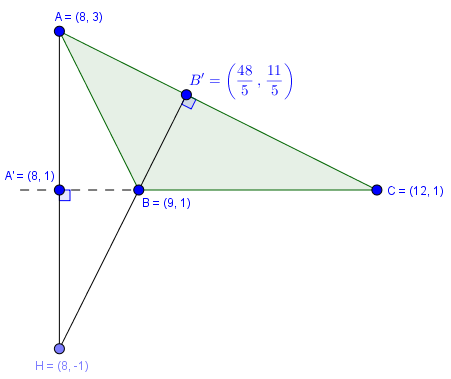
Ví dụ 3. Cho tam giác $ABC$ có $A(8, 3), B(9, 1), C(12, 1)$, tìm tọa độ trực tâm $H$ của tam giác $ABC$

Dễ thấy phương trình đường cao $(AA’): x-8=0$

Dễ thấy phương trình đường cao $(BB’): 2x-y-17=0$

Giả hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x-8=0\\ 2x-y-17=0 \end{array}\right.$ được nghiệm là $(8, -1)$

Vậy tọa độ trực tâm $H$ của tam giác $ABC$ là $(8, -1)$

#4. Lời kết

Như vậy là qua bài viết này thì mình tin là bạn đã biết cách tìm tọa độ trực tâm của tam giác rồi phải không nào?!

Và qua Ví dụ 2 bên trên ta nhận thấy rằng, trong hình học giải tích vẫn nên vẽ hình ra giấy, việc quan sát hình vẽ sẽ giúp chúng ta dễ dàng phát hiện ra các tính chất đặc biệt (nếu có).

Sau khi phát hiện được tính chất đặc biệt (thật ra chỉ là dự đoán), bạn cần chứng minh “là có” trước khi áp dụng các công thức đặc biệt.

Nếu chứng minh được thì việc giải bài toán sẽ đơn giản hơn và nhanh hơn khá nhiều. Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Kiên Nguyễn – Blogchiasekienthuc.com