Cách viết phương trình đường trung trực của tam giác

Xin chào tất cả các bạn, tiếp nối mạch kiến thức về các phương trình đường thẳng đồng quy trong tam giác thì hôm nay mình sẽ hướng dẫn cho các bạn cách viết ba phương trình đường trung trực ba cạnh của tam giác.

Đầu tiên là mình sẽ nhắc lại khái niệm về đường trung trực, tiếp theo mình sẽ chỉ ra điều kiện cần và đủ để viết được phương trình đường trung trực, tiếp theo nữa là các bước viết phương trình đường trung trực và cuối cùng là ví dụ minh họa cho các bạn dễ hiểu.

Okay, let’s go…

#1. Đường trung trực là đường thẳng như thế nào?

Vâng, khi nhắc đến đường trung trực thì mặc định chúng ta sẽ tự hiểu là đường trung trực của tam giác.

Đường trung trực là đường thẳng đi qua trung điểm một cạnh và vuông góc với cạnh đó.

Tam giác nào cũng có đúng ba đường trung trực.

Ba đường trung trực đồng quy tại một điểm, điểm này cách đều ba đỉnh của tam giác, nói cách khác, điểm này chính là tâm đường tròn ngoại tiếp tam giác.

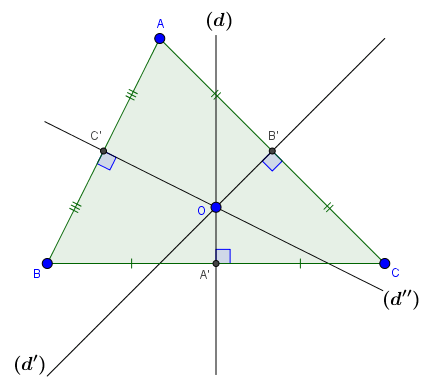
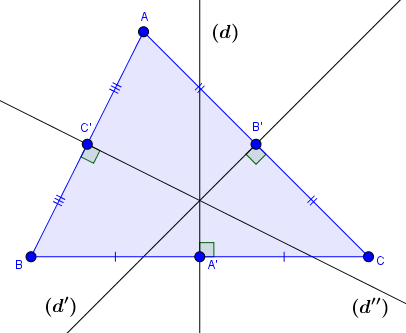
Tam giác $ABC$ có $(d), (d’), (d’’)$ lần lượt là ba đường trung trực của ba cạnh $BC, CA, AB$

Giao điểm $O$ của ba đường trung trực chính là tâm của đường tròn ngoại tiếp tam giác.

#2. Để viết được phương trình đường trung trực chúng ta cần?

Để viết được phương trình đường trung trực thì chúng ta cần một điểm đi qua và một véc tơ chỉ phương.

Cụ thể chúng ta sẽ chọn:

• Điểm đi qua là trung điểm của cạnh cần viết phương trình đường trung trực.
• Véc tơ chỉ phương là véc tơ pháp tuyến của phương trình đường thẳng chứa cạnh cần viết phương trình đường trung trực.

#3. Các bước viết phương trình đường trung trực của tam giác

Cho tam giác $ABC$ có $A(x_a, y_a), B(x_b, y_b), C(x_c, y_c)$, viết phương trình các đường trung trực của tam giác $ABC$

Giả sử $(d), (d’), (d”)$ lần lượt là ba đường trung trực của ba cạnh $BC, CA, AB$

Bước 1. Tìm $A’, B’, C’$ biết $A’, B’, C’$ lần lượt là trung điểm ba cạnh $BC, CA, AB$

$A’(\frac{x_b+x_c}{2}, \frac{y_b+y_c}{2})$

$B’(\frac{x_c+x_a}{2}, \frac{y_c+y_a}{2})$

$C’(\frac{x_a+x_b}{2}, \frac{y_a+y_b}{2})$

Bước 2. Tìm tọa độ véc tơ $\overrightarrow{BC}$

$\overrightarrow{BC}=(x_c-x_b, y_c-y_b)$

Bước 3. Tìm véc tơ chỉ phương của $(d)$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Dễ thấy véc tơ chỉ phương của $(d)$ là $(-(y_c-y_b), x_c-x_b)$

Bước 4. Phương trình đường trung trực $(d)$ đi qua điểm $A’(\frac{x_b+x_c}{2}, \frac{y_b+y_c}{2})$ và nhận véc tơ $(-(y_c-y_b), x_c-x_b)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=\frac{x_b+x_c}{2}+(-(y_c-y_b))t \\ y=\frac{y_b+y_c}{2}+(x_c-x_b)t\end{array}\right.$

Bước 5. Thực hiện tương tự Bước 2 – Bước 4 để viết phương trình đường trung trực $(d’), (d”)$

Giải thích thêm Bước 2 và Bước 3:

Vì $\overrightarrow{BC}=(x_c-x_b, y_c-y_b)$ là véc tơ chỉ phương của đường thẳng $(BC)$ nên véc tơ pháp tuyến của đường thẳng $(BC)$ là $(-(y_c-y_b), x_c-x_b)$

Mặc khác, véc tơ pháp tuyến của đường thẳng $(BC)$ lại là véc tơ chỉ phương của $(d)$

Vậy véc tơ chỉ phương của $(d)$ chính là $(-(y_c-y_b), x_c-x_b)$

#4. Bài tập ví dụ

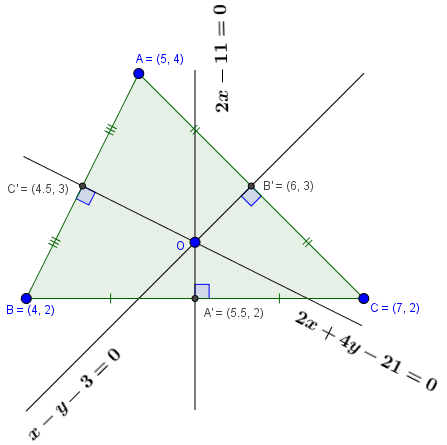
Cho tam giác $ABC$ có $A(5,4), B(4, 2), C(7, 2)$, viết phương trình ba đường trung trực của ba cạnh của tam giác $ABC$

Gọi $A’, B’, C’$ lần lượt là trung điểm các cạnh $BC, CA, AB$

$A’\left(\frac{4+7}{2}, \frac{2+2}{2}\right)=\left(\frac{11}{2}, 2\right)$

$B’\left(\frac{7+5}{2}, \frac{2+4}{2}\right)=(6, 3)$

$C’\left(\frac{5+4}{2}, \frac{4+2}{2}\right)=\left(\frac{9}{2}, 3\right)$

Dễ thấy, véc tơ $\overrightarrow{BC}=(3, 0)$ là véc tơ chỉ phương của đường thẳng $(BC)$

Suy ra véc tơ chỉ phương của đường trung trực của cạnh $BC$ là $(0, 3)$

=> Phương trình đường trung trực đi qua điểm $A’=\left(\frac{11}{2}, 2\right)$ và nhận véc tơ $(0, 3)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=\frac{11}{2} \\ y=2+3t\end{array}\right.$

Dễ thấy véc tơ $\overrightarrow{CA}=(-2, 2)$ là véc tơ chỉ phương của đường thẳng $(CA)$

Suy ra véc tơ chỉ phương của đường trung trực của cạnh $CA$ là $(-2, -2)$

=> Phương trình đường trung trực đi qua điểm $B’=(6, 3)$ và nhận véc tơ $(-2, -2)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=6-2t \\ y=3-2t\end{array}\right.$

Dễ thấy véc tơ $\overrightarrow{AB}=(-1, -2)$ là véc tơ chỉ phương của đường thẳng $(AB)$

Suy ra véc tơ chỉ phương của đường trung trực của cạnh $AB$ là $(2, -1)$

=> Phương trình đường trung trực đi qua điểm $C’=\left(\frac{9}{2}, 3\right)$ và nhận véc tơ $(2, -1)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=\frac{9}{2}+2t \\ y=3-t\end{array}\right.$

#5. Lời kết

Vâng, như vậy là qua bài viết này thì mình tin là bạn đã biết cách để viết phương trình đường trung trực của tam giác rồi.

Thay cho lời kết thì mình xin gửi đến các bạn một lời giải thích như sau:

Nếu để ý các bạn sẽ thấy phương trình đường trung trực mà mình kết luận “khác” với phương trình đường trung trực trên hình vẽ.

Thật ra, chúng chỉ khác nhau về mặt hình thức, bản chất vẫn giống nhau, vẫn là một phương trình đường trung trực. Cụ thể là phương trình đường trung trực ở kết luận được viết dưới dạng tham số, còn ở hình vẽ được viết phương trình dạng tổng quát.

Okay, hi vọng là bạn sẽ thích bài viết này. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn