4 đường thẳng đồng quy trong tam giác, bạn còn nhớ không?

Xin chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu về các đường thẳng đồng quy trong tam giác.

Về cơ bản thì có bốn loại đường thẳng đồng quy, đó là: đường trung tuyến, đường cao, đường trung trực và đường phân giác.

Việc giới thiệu một cách đầy đủ về bốn loại đường trên trong cùng một bài viết là không khả thi, vì vậy mình chỉ phát biểu định nghĩa, vẽ hình minh họa và trình bày một vài kiến thức cơ bản có liên quan trực tiếp mà thôi.

Mục đích của bài viết này rất đơn giản, khi đọc đến tên của nó thì bạn có thể vẽ được nó một cách chính xác. Như vậy là rất ok rồi !

#1. Đường trung tuyến của tam giác là gì?

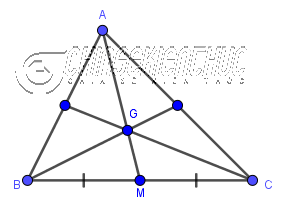
+ Đường trung tuyến của một tam giác là một đường thẳng đi qua đỉnh và trung điểm của cạnh đối diện. Mỗi tam giác sẽ có 3 đường trung tuyến.

Ba đường trung tuyến trong một tam giác luôn đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

Trọng tâm của tam giác cách đỉnh một khoảng bằng hai phần ba độ dài đường trung tuyến tương ứng.

• AM là đường trung tuyến của tam giác ABC, nó đi qua đỉnh A và trung điểm M của cạnh BC
• G là trọng tâm của tam giác ABC
• $AG=\frac{2}{3}AM$

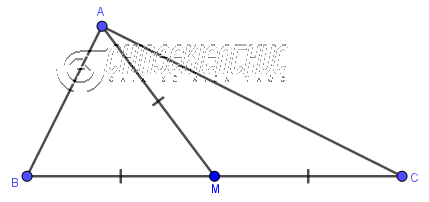
+ Trong một tam giác vuông thì độ dài đường trung tuyến ứng với cạnh huyền bằng ½ độ dài cạnh huyền.

AM là đường trung tuyến của tam giác vuông ABC (vuông ở A) nên $AM=\frac{1}{2}BC$

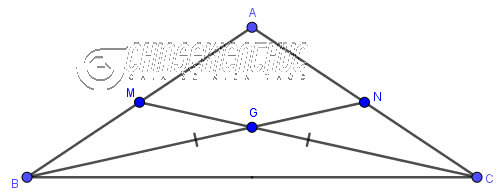
+ Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Như hình bên trên thì BN, CM là hai đường trung tuyến của tam giác cân ABC (cân ở A) nên BN=CM

#2. Đường cao của tam giác là gì?

Đường cao của tam giác là một đường thẳng đi qua đỉnh và vuông góc với cạnh đối diện.

Hay nói cách khác: Đường cao của một tam giác là đoạn thẳng được kẻ từ một đỉnh và vuông góc với cạnh đối diện của tam giác đó.

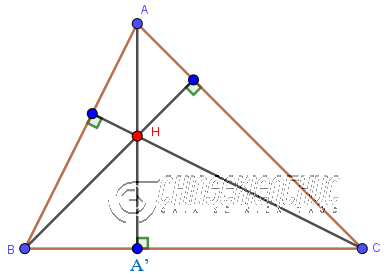
Ba đường cao trong một tam giác luôn đồng quy tại một điểm, điểm này được gọi là trực tâm của tam giác.

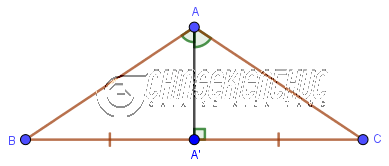
• AA’ là đường cao đi qua đỉnh A và vuông góc với cạnh đối diện BC tại A’
• G là trực tâm của tam giác ABC

+ Trong một tam giác cân đường cao đi qua đỉnh cũng là đường trung tuyến, đường trung trực và đường phân giác của tam giác đó.

Như hình bên trên thì đường cao AA’ đi qua đỉnh A của tam giác cân ABC (cân ở A) nên AA’ cũng là đường trung tuyến, đường trung trực và đường phân giác.

+ Trong một tam giác có hai trong bốn loại đường (trung tuyến, đường cao, trung trực, phân giác) trùng nhau thì tam giác đó là tam giác cân => bạn có thể vận dụng kiến thức này vào việc chứng minh tam giác đã cho là tam giác cân.

#3. Đường trung trực của tam giác là gì?

Đường trung trực của tam giác là đường thẳng đi qua trung điểm của một cạnh và vuông góc với cạnh đó.

Ba đường trung trực trong một tam giác luôn đồng quy tại một điểm, điểm này cách đều ba đỉnh của tam giác và là tâm đường tròn ngoại tiếp tam giác.

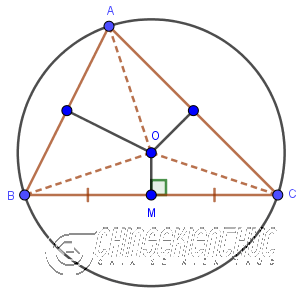
• OM là đường trung trực tương ứng với cạnh BC
• O là tâm đường tròn ngoại tiếp tam giác ABC
• OA = OB = OC

+ Trong một tam giác cân đường trung trực ứng với cạnh đáy cũng là đường trung tuyến.

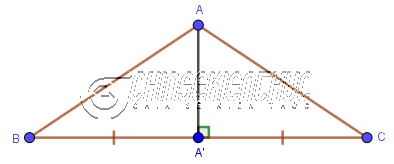
Như hình bên trên thì AA’ là đường trung trực của tam giác cân ABC (cân tại A) nên cũng là đường trung tuyến

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

#4. Đường phân giác của tam giác là gì?

Trước khi đến với khái niệm đường phân giác thì chúng ta sẽ tìm hiểu về khái niệm của tia phân giác trước.

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Tia phân giác của $\hat{A}$ cắt cạnh đối diện BC tại điểm A’, khi đó AA’ được gọi là đường phân giác của $\hat{A}$

Ba đường phân giác trong tam giác luôn đồng quy tại một điểm, điểm này cách đều ba cạnh của tam giác và là tâm đường tròn nội tiếp tam giác

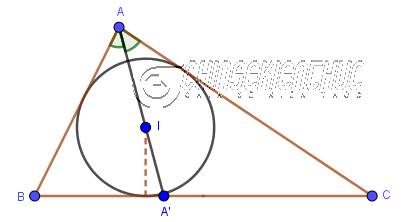
• AA’ là một đường phân giác tương ứng với cạnh BC
• I là tâm đường tròn nội tiếp

#5. Lời kết

Vâng, như vậy là qua bài viết này thì bạn đã biết hoặc nhớ lại tính chất và định nghĩa của đường trung tuyến, đường cao, đường trung trực, đường phân giác trong một tam giác rồi đúng không.

• Trong một tam giác đều thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp sẽ trùng nhau.
• Trong một tam giác bất kỳ thì trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác luôn nằm trên một đường thẳng, hay nói cách khác là thẳng hàng nhau.

Đó là đôi lời mở rộng kiến thức mà mình muốn gửi đến các bạn.

Hi vọng bài viết này sẽ hữu ích với bạn, chúc các bạn học tập tốt, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 2 cách tính độ dài cạnh huyền trong tam giác vuông (rất dễ)
• Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com