2 cách tính độ dài cạnh huyền trong tam giác vuông (rất dễ)

Xin chào tất cả các bạn, trong bài viết này chúng ta sẽ cùng nhau tìm hiểu về cách tính độ dài cạnh huyền trong tam giác vuông.

Mặc dù có khá nhiều cách tính khác nhưng trong phạm vi ngắn gọn của bài viết này, mình chỉ giới thiệu hai cách đơn giản nhất, cũng như được áp dụng nhiều nhất đó là định lí Py-ta-go và định lí hàm SIN.

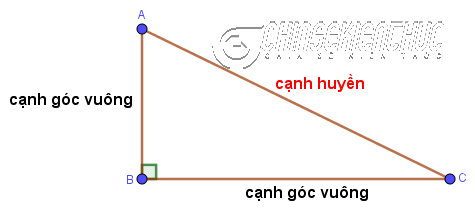
I. Cạnh huyền là cạnh như thế nào?

Trước hết chúng ta cần biết rằng cạnh huyền chỉ có trong tam giác vuông, tam giác thường không bao giờ có cạnh này.

• Cạnh huyền là cạnh đối diện với góc vuông.
• Trong một tam giác vuông bất kì ta luôn có một cạnh huyền và hai cạnh góc vuông.
• Cạnh huyền là cạnh dài nhất.

Tùy thuộc vào giả thuyết của bài toán mà chúng ta sẽ lựa chọn và áp dụng công thức cho phù hợp nhất.

Trường hợp #1: Tính độ dài cạnh huyền biết độ dài hai cạnh góc vuông

Khi giả thuyết của bài toán đã cho độ dài hai cạnh góc vuông thì để tính độ dài của cạnh huyền chúng ta sẽ dựa vào định lí Py-ta-go

Trong một tam giác vuông bất kì chúng ta luôn có bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

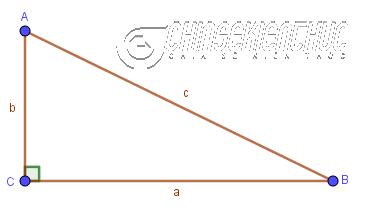
Xét tam giác vuông ABC (vuông ở góc C) có CB=a, CA=b, AB=c

Sử dụng công thức: $c^2=a^2+b^2$

Trong đó:

• c là độ dài của cạnh huyền AB
• a là độ dài của cạnh góc vuông CB
• b là độ dài của cạnh góc vuông CA

=> Như vậy, để tính được độ dài của cạnh huyền chúng ta sẽ lấy căn bậc hai của tổng bình phương hai cạnh góc vuông.

Cụ thể là: $c=\sqrt{a^2+b^2}$

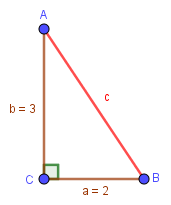
Ví dụ 1: Cho tam giác ABC có CB=2, CA=3 và góc ACB bằng 90 độ. Tính độ dài cạnh AB

Chúng ta có nhận xét tam giác đã cho là tam giác vuông (vuông ở góc C) và độ dài cạnh cần tính chính là độ cạnh huyền.

Lời Giải:

Áp dụng công thức $c=\sqrt{a^2+b^2}$ vào tam giác đã cho ta được $\sqrt{2^2+3^2}=\sqrt{13}$

Vậy độ dài của cạnh cần tìm là $\sqrt{13}$ ĐVĐD

Trường hợp #2: Tính độ dài cạnh huyền biết độ dài một cạnh góc vuông và độ lớn góc đối

Khi giả thuyết của bài toán đã cho độ dài một cạnh góc vuông và độ lớn góc đối thì để tính được độ dài của cạnh huyền chúng ta sẽ dựa định lí hàm SIN.

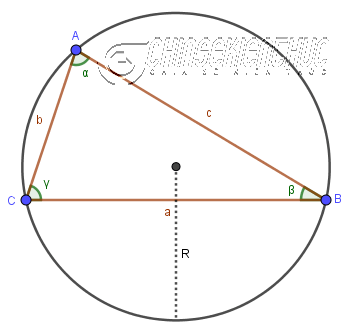
Định lý hàm SIN biểu thị mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với giá trị SIN của các góc tương ứng và bán kính đường tròn ngoại tiếp tam giác.

Sử dụng công thức: $\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}=2R$

Trong đó:

• $a=CB, b=CA, c=AB$
• $\alpha=\widehat{CAB}, \beta=\widehat{ABC}, \gamma=\widehat{BCA}$
• R độ dài bán kính đường tròn ngoại tiếp tam giác

Vì định lí hàm SIN áp dụng được với tam giác thường nên tất nhiên ta có thể áp dụng được với tam giác vuông.

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Khả năng ứng dụng của định lí này là rất cao, tuy nhiên, trong phạm vi ngắn gọn của bài viết này mình chỉ hướng dẫn các bạn ứng dụng nó để tính độ dài cạnh huyền của tam giác vuông mà thôi.

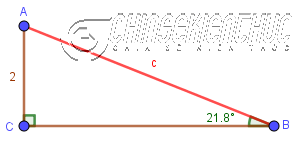
Ví dụ 2. Cho tam giác vuông ABC (vuông ở góc C) có CA=2 và góc ABC bằng 21.8 độ. Tính độ dài cạnh huyền AB

Để cho dễ chúng ta nên viết định lí hàm SIN một cách đầy đủ, rồi mới đọc lại bài toán xem bài toán cho gì, yêu cầu tìm gì?

• Bài toán đã cho $b=2, \beta=21.8^o$
• Bài toán yêu cầu tìm c (độ dài cạnh huyền AB)

Lời Giải:

Áp dụng định lí hàm SIN vào tam giác đã cho ta được $\frac{a}{\sin \alpha}=\frac{2}{\sin 21.8^o}=\frac{c}{\sin 90^o}=2R$ hay $\frac{2}{\sin 21.8^o}=\frac{c}{\sin 90^o}$

Suy ra $c=\frac{2.\sin90^o}{\sin21.8^o} \approx 5.3$

=> Vậy độ dài cạnh cần tìm gần bằng 5.3 ĐVĐD

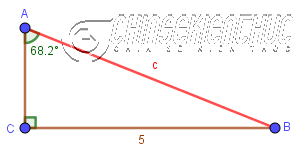
Ví dụ 3. Cho tam giác vuông ABC (vuông góc ở C) có CB=5 và góc CAB bằng 68.2 độ. Tính độ dài cạnh huyền AB

Ví dụ 3 hoàn toàn tương tự như Ví dụ 2 (giả thuyết khác nhau nhưng kết quả sau giống nhau)

Mục đích của ví dụ này là giúp bạn ghi nhớ và rèn luyện kĩ năng áp dụng vào từng bài toán cụ thể.

Lời Giải:

Áp dụng định lí hàm SIN vào tam giác đã cho ta được $\frac{5}{\sin 68.2^o}=\frac{c}{\sin 90^o}$

=> $c=\frac{5.\sin90^o}{\sin68.2^o} \approx 5.3$

Vậy độ dài cạnh huyền cần tìm gần bằng 5.3 ĐVĐD

II. Lời kết

Thay cho lời kết, mình sẽ giới thiệu cho các bạn một số trường hợp đặc biệt, khi tam giác vuông rơi vào một trong các trường hợp bên dưới thì cách tính độ cạnh huyền sẽ đơn giản hơn nữa.

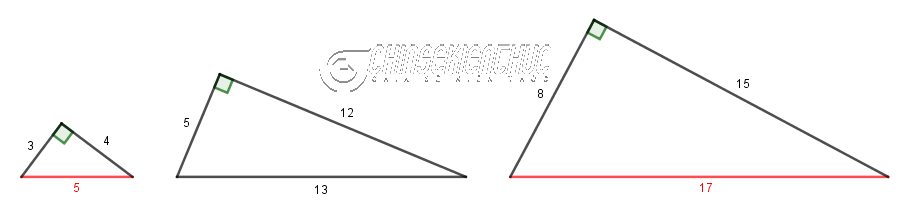
• Khi độ dài hai cạnh góc luôn là 3, 4 hoặc 5, 12 hoặc 8, 15 hoặc … thì độ dài cạnh huyền lần lượt là 5, 13, 17, … (bộ ba Py-ta-go)

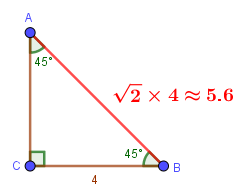
• Khi có độ lớn hai góc là 45, 45 thì độ dài cạnh huyền sẽ bằng tích của căn hai và độ dài cạnh góc vuông

Okay, như vậy là qua bài viết này thì mình tin là bạn đã biết cách để tính độ dài cạnh huyền trong tam giác vuông rồi đúng không 😀 Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tính chu vi, diện tích của hình tròn và hình quạt tròn
• Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ hiểu)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com