Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Dưới đây là các công thức cơ bản nhất của mảng kiến thức Hình học Giải tích trên mặt phẳng..
Nội dung của bài viết cũng là nội dung chính của Chương III – Phương pháp tọa độ trên mặt phẳng, Sách giáo khoa Hình học 10 Nâng cao.
Mục đích mình viết bài viết này là để giúp các bạn có cái nhìn tổng quát nhất về Chương III, chuẩn bị cho bài kiểm tra giữa kỳ và xa hơn là kiểm tra cuối kỳ.
Mục Lục Nội Dung
- #1. Định nghĩa véc tơ pháp tuyến
- #2. Định nghĩa véc tơ chỉ phương
- #3. Định nghĩa Elip, Hypebol, Parabol và Cônic
- #4. Phương trình đường thẳng
- #5. Phương trình đường tròn
- #6. Phương trình chính tắc của đường Elip
- #7. Phương trình chính tắc của đường Hypebol
- #8. Phương trình chính tắc của đường Parabol
- #9. Công thức tính khoảng cách từ một điểm đến một đường thẳng
- #10. Khi nào đường thẳng tiếp xúc với đường tròn
- #11. Công thức tính góc giữa hai đường thẳng
- #12. Lời kết
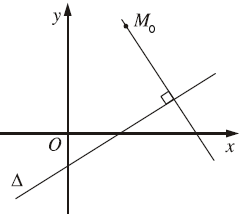
#1. Định nghĩa véc tơ pháp tuyến
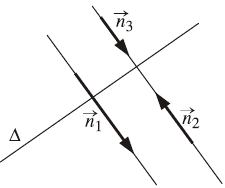
$\vec{n}$ được gọi là vec tơ pháp tuyến của đường thẳng $\Delta$ nếu $\vec{n} \neq \overrightarrow{0}$ và giá của $\vec{n}$ vuông góc với $\Delta$.
Như hình bên trên: $\vec{n}_1, \vec{n}_2, \vec{n}_3$ là những vectơ pháp tuyến của $\Delta$
#2. Định nghĩa véc tơ chỉ phương
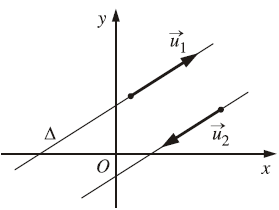
$\vec{u}$ được gọi là vec tơ chỉ phương của đường thẳng $\Delta$ nếu $\vec{u} \neq \overrightarrow{0}$ và giá của $\vec{u}$ song song hoặc trùng với $\Delta$
Như các bạn thấy ở hình bên trên: $\vec{u}_1, \vec{u}_2$ là các vectơ chỉ phương của đường thẳng $\Delta$
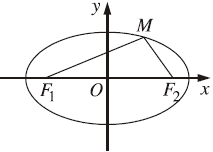
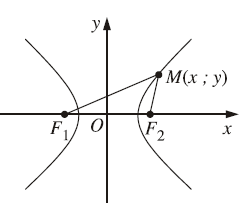
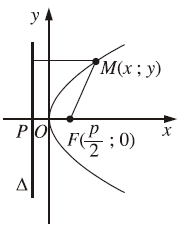
#3. Định nghĩa Elip, Hypebol, Parabol và Cônic
Elip là tập hợp các điểm $M$ thoả mãn $M F_1+M F_2=2 a$ với $F_1 F_2=2 c$ và $0<c<\mathrm{a}$
Hypebol là tập các điểm $M$ thoả mãn $\left|M F_1-M F_2\right|=2 a$ với $F_1 F_2=2 c$ và $c>a>0$
Parabol là tập các điểm $M$ thoả mãn $M F=d(M ; \Delta)$ với $d(F ; \Delta)=p>0$
Đường Cônic là tập các điểm $M$ thoả mãn $\frac{M F}{d(M ; \Delta)}=e>0$
- Nếu $e<1$ thì đường Cônic là Elip
- Nếu $e=1$ thì đường Cônic là Parabol
- Nếu $e>1$ thì đường Cônic là Hypebol
#4. Phương trình đường thẳng
+) Dạng tổng quát $a x+b y+c=0$ với $a^2+b^2 \neq 0$
Ở dạng tổng quát đường thẳng có một vec tơ pháp tuyến là $\vec{n}(a ; b)$
+) Dạng tham số $\left\{\begin{array}{l} x=x_0+a t \\ y=y_0+b t
\end{array} \right.$ với $a^2+b^2 \neq 0$
+) Dạng chính tắc $\frac{x-x_0}{a}=\frac{y-y_0}{b}$ với $a \neq 0$ và $b \neq 0$
Ở dạng tham số và dạng chính tắc thì đường thẳng đi qua điểm $\left(x_0 ; y_0\right)$ và có vec tơ chỉ phương $\vec{u}=(a; b)$
#5. Phương trình đường tròn
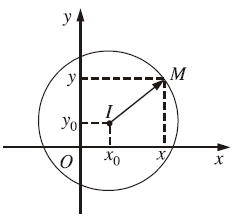
+) Đường tròn tâm $I\left(x_0 ; y_0\right)$ và bán kính $R$ có phương trình là $\left(x-x_0\right)^2+\left(y-y_0\right)^2=R^2$
+) Phương trình $x^2+y^2+2 a x+2 b y+c=0$ với $a^2+b^2-c>0$ cũng được gọi là phương trình đường tròn
Lúc này phương trình đường tròn $x^2+y^2+2 a x+2 b y+c=0$ có tâm là $I(-a ;-b)$ và bán kính là $R=\sqrt{a^2+b^2-c}$
#6. Phương trình chính tắc của đường Elip
Phương trình Elip có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với $a>b>0$
- Dễ thấy $c^2=a^2-b^2$ suy ra các tiêu điểm là $F_1(-c ; 0)$ và $F_2(c ; 0)$
- Trục lớn $2 a$
- Trục bé $2 b$
- Tâm sai $e=\frac{c}{a}<1$
- Đường chuẩn $x=\pm \frac{a}{e}$
#7. Phương trình chính tắc của đường Hypebol
Phương trình Hypebol là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ với $a>0, b>0$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
- Dễ thấy $c^2=a^2+b^2$ suy ra các tiêu điểm là $F_1(-c ; 0)$ và $F_2(c ; 0)$
- Trục thực $2 a$
- Trục ảo $2 b$
- Tâm sai $e=\frac{c}{a}>1$
- Đường chuẩn $x=\pm \frac{a}{e}$
- Tiệm cận $y=\pm \frac{b}{a} x$
#8. Phương trình chính tắc của đường Parabol
Phương trình Parabol là $y^2=2 p x$ với $p>0$
- Tiêu điểm $F\left(\frac{p}{2} ; 0\right)$
- Tâm sai $e=1$
- Đường chuẩn $x=-\frac{p}{2}$
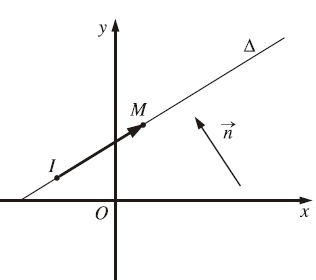
#9. Công thức tính khoảng cách từ một điểm đến một đường thẳng
Khoảng cách từ điểm $M\left(x_0 ; y_0\right)$ đến đường thẳng $\Delta: a x+b y+c=0$ được tính theo công thức:
- $d(M ; \Delta)=\frac{\left|a x_0+b y_0+c\right|}{\sqrt{a^2+b^2}}$
Xem thêm:
Cách tính khoảng cách từ một điểm đến một đường thẳng
#10. Khi nào đường thẳng tiếp xúc với đường tròn
Đường thẳng $\Delta: a x+b y+c=0$ tiếp xúc với đường tròn $(I ; R)$ khi và chỉ khi $d(I ; \Delta)=R$
#11. Công thức tính góc giữa hai đường thẳng
Góc giữa hai đường thẳng $\Delta_1: a_1 x+b_1 y+c_1=0$ và $\Delta_2: a_2 x+b_2 y+c_2=0$ được xác định bởi công thức:
- $\cos \left(\Delta_1, \Delta_2\right)=\frac{\left|a_1 a_2+b_1 b_2\right|}{\sqrt{a_1^2+b_1^2} \cdot \sqrt{a_2^2+b_2^2}}$
#12. Lời kết
Qua bài viết này cùng với những bài viết mà mình đã liên kết sẽ giúp các bạn giải bài tập một cách chính xác và nhanh chóng hơn. Bạn có thể dễ dàng giải được:
- Phương trình đường thẳng, phương trình đường tròn
- Khoảng cách giữa một điểm và một đường thẳng
- Độ lớn của góc tạo bởi hai đường thẳng…
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
