Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Xin chào tất cả các bạn, để tiếp nối mạch kiến thức về phương trình đường phân giác trong tam giác thì trong bài viết ngày hôm nay, mình sẽ hướng dẫn cho các bạn cách viết phương trình đường tròn nội tiếp tam giác
Đầu tiên mình sẽ nhắc lại khái niệm, tiếp theo là các bước viết phương trình và cuối cùng là ví dụ minh họa.
Đọc thêm:
Cách viết phương trình đường tròn ngoại tiếp tam giác
Mục Lục Nội Dung
#1. Kiến thức có liên quan đến đường tròn nội tiếp tam giác
Dưới đây là một số kiến thức cơ bản bạn cần phải nắm được nếu muốn viết được phương trình đường tròn nội tiếp tam giác.
1.1. Khái niệm đường tròn nội tiếp
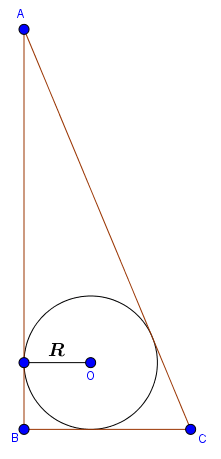
Đường tròn nội tiếp tam giác là đường tròn nhỏ nhất nằm trong tam giác và tiếp xúc với cả ba cạnh của tam giác.
Ví dụ như hình bên dưới: Đường tròn tâm O bán kính R nội tiếp tam giác ABC, hoặc tam giác ABC ngoại tiếp đường tròn tâm O bán kính R
Chú ý:
Mỗi tam giác có một và chỉ một đường tròn nội tiếp.
1.2. Đường tròn nội tiếp xác định khi nào
Một đường tròn bất kỳ hoàn toàn xác định (viết được, vẽ được) khi biết tâm và bán kính, hoặc biết được ba điểm thuộc đường tròn.
Như vậy suy ra, muốn viết được phương trình đường tròn nội tiếp tam giác thì chúng ta cần phải biết tâm và bán kính của nó.
- Tâm
Icủa đường tròn nội tiếp tam giác là giao điểm của hai đường phân giác. - Bán kính là
IJvớiJlà hình chiếu vuông góc của I lên một cạnh của tam giác.
#2. Các bước viết phương trình đường tròn nội tiếp tam giác
Viết phương trình đường tròn nội tiếp tam giác ABC
Bước 1. Viết phương trình đường phân giác của $\hat{A}$
Giả sử phương trình là $A_1x+B_1y+C_1=0$
Bước 2. Viết phương trình đường phân giác của $\hat{B}$
Giả sử phương trình là $A_2x+B_2y+C_2=0$
Bước 3. Nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_1x+B_1y+C_1=0 \\ A_2x+B_2y+C_2=0\end{array}\right.$ là tâm của đường tròn nội tiếp
Giả sử tâm là $I(x_i, y_i)$
Bước 4. Viết phương trình đường thẳng đi qua hai điểm A, B
Giả sử phương trình đường thẳng là $A_3x+B_3y+C_3=0$
Bước 5. Viết phương trình đường thẳng đi qua tâm $I$ và vuông góc với đường thẳng $A_3x+B_3y+C_3=0$
Giả sử phương trình đường thẳng là $A_4x+B_4y+C_4=0$
Bước 6. Nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_3x+B_3y+C_3=0 \\ A_4x+B_4y+C_4=0\end{array}\right.$ là hình chiếu vuông góc của tâm I lên đường thẳng $A_3x+B_3y+C_3=0$
Giả sử hình chiếu là $J(x_j, y_j)$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Bước 7. Khoảng cách giữa hai điểm I, J chính là bán kính của đường tròn nội tiếp $\sqrt{(x_j-x_i)^2+(y_j-y_i)^2}$
Giả sử bán kính là R
Bước 8. Phương trình đường tròn nội tiếp tam giác ABC có dạng $(x-x_i)^2+(y-y_i)^2=R^2$
#3. Bài tập ví dụ viết phương trình đường tròn nội tiếp tam giác
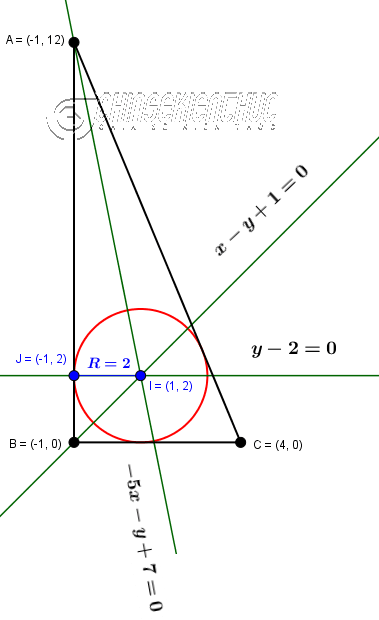
Viết phương trình đường tròn nội tiếp tam giác ABC biết $A(-1,12), B(-1,0), C(4,0)$
Dễ thấy, phương trình đường phân giác của $\hat{A}$ và $\hat{B}$ lần lượt là $-5x-y+7=0$ và $x-y+1=0$
Xem thêm:
Cách viết phương trình đường phân giác
Tâm của đường tròn nội tiếp tam giác sẽ là nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}-5x-y+7=0 \\ x-y+1=0 \end{array}\right.$, hệ có một nghiệm duy nhất là $(1,2)$
Suy ra tâm của đường tròn là $I(1,2)$
Dễ thấy $\overrightarrow{AB}=(0, -12)$
Phương trình đường thẳng đi qua điểm A và nhận véc tơ $\overrightarrow{AB}=(0, -12)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l} x=-1 \\ y=12-12t \end{array}\right. \Leftrightarrow x+1=0$
Phương trình đường thẳng đi qua tâm I và vuông góc với đường thẳng $x+1=0$ là $y-2=0$
Giao điểm của $x+1=0$ và $y-2=0$ là nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x+1=0 \\ y-2=0 \end{array}\right.$, hệ có một nghiệm duy nhất là $J(-1,2)$
Bán kính của đường tròn nội tiếp tam giác là $IJ=\sqrt{(-1-1)^2+(2-2)^2}=2$
Vậy => phương trình đường tròn nội tiếp tam giác ABC là $(x-1)^2+(y-2)^2=4$
#4. Lời kết
Để viết được phương trình đường tròn nội tiếp tam giác thì mấu chốt là bạn phải xác định được tâm và bán kính.
Để xác định được tâm và bán kính một nhanh chóng nhất thì bạn nên xem thêm cách viết phương trình đường thẳng, cách giải phương trình bậc hai một ẩn và đặc biệt là cách viết phương trình đường phân giác trong tam giác..
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
