Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Nếu bạn đã biết cách viết phương trình đường trung trực thì việc viết phương trình đường cao của tam giác sẽ dễ dàng hơn rất nhiều, bạn chỉ cần “thay” điểm đi qua là xong.
Cụ thể thì…
- Ở phương trình đường trung trực, điểm đi qua là trung điểm của cạnh vuông góc.
- Ở phương trình đường cao, điểm đi qua là đỉnh đối diện với cạnh vuông góc.
Mục Lục Nội Dung
#1. Mối quan hệ giữa véc tơ chỉ phương và véc tơ pháp tuyến
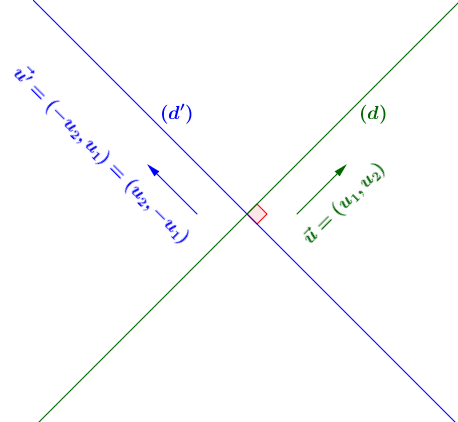
Cho đường thẳng $(d)$ có véc tơ chỉ phương $\vec{u}=(u_1, u_2)$
Cho đường thẳng $(d’)$ vuông góc với đường thẳng $(d)$
Lúc này véc tơ pháp tuyến của đường thẳng $(d)$ chính là véc tơ chỉ phương của đường thẳng $(d’)$
Cụ thể thì véc tơ chỉ phương của đường thẳng $(d’)$ là $\vec{u’}=(-u_2, u_1)$ hoặc $\vec{u’}=(u_2, -u_1)$
Chú ý:
Một đường thẳng bất kỳ sẽ có vô số véc tơ chỉ phương, vậy nên suy ra cũng có vô số véc tơ pháp tuyến.
#2. Các bước viết phương trình đường cao
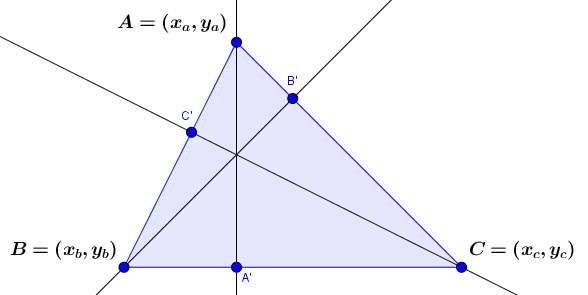
Cho tam giác $ABC$ có $A(x_a, y_a), B(x_b, y_b), C(x_c, y_c)$, viết phương trình các đường cao của tam giác $ABC$
Gọi $AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$
Các bước viết phương trình đường cao $AA’$
Dễ thấy véc tơ $\overrightarrow{BC}=(x_c-x_b, y_c-y_b)$ là véc tơ chỉ phương của đường thẳng $BC$
Suy ra véc tơ chỉ phương của đường cao $AA’$ là $(-(y_c-y_b), x_c-x_b)$
Vậy phương trình đường cao $AA’$ có điểm đi qua $A(x_a, y_a)$ và nhận véc tơ $(-(y_c-y_b), x_c-x_b)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=x_a+(-(y_c-y_b))t \\ y=y_a+(x_c-x_b)t\end{array}\right.$
Các bước viết phương trình đường cao $BB’$
Dễ thấy véc tơ $\overrightarrow{CA}=(x_a-x_c, y_a-y_c)$ là véc tơ chỉ phương của đường thẳng $CA$
Suy ra véc tơ chỉ phương của đường cao $BB’$ là $(-(y_a-y_c), x_a-x_c)$
Vậy phương trình đường cao $BB’$ có điểm đi qua $B(x_b, y_b)$ và nhận véc tơ $(-(y_a-y_c), x_a-x_c)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=x_b+(-(y_a-y_c))t \\ y=y_b+(x_a-x_c)t\end{array}\right.$
Các bước viết phương trình cao $CC’$
Dễ thấy véc tơ $\overrightarrow{AB}=(x_b-x_a, y_b-y_a)$ là véc tơ chỉ phương của đường thẳng $AB$
Suy ra véc tơ chỉ phương của đường cao $CC’$ là $(-(y_b-y_a), x_b-x_a)$
Vậy phương trình đường cao $CC’$ có điểm đi qua $C(x_c, y_c)$ và nhận véc tơ $(-(y_b-y_a), x_b-x_a)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=x_c+(-(y_b-y_a))t \\ y=y_c+(x_b-x_a)t\end{array}\right.$
#3. Bài tập ví dụ về phương trình đường cao
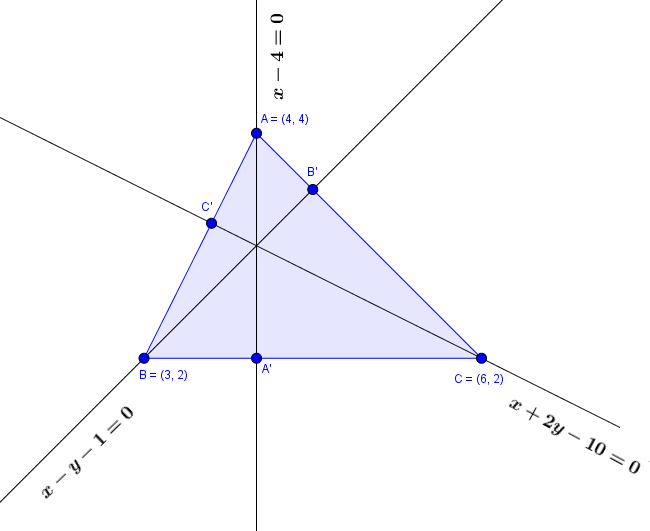
Cho tam giác $ABC$ có $A(4, 4), B(3, 2), C(6,2)$, viết phương trình các đường cao của tam giác $ABC$
Gọi $AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$
Phương trình đường cao $AA’$
Dễ thấy véc tơ $\overrightarrow{BC}=(3 ,0)$ là véc tơ chỉ phương của đường thẳng $BC$
Suy ra véc tơ chỉ phương của đường cao $AA’$ là $(0, 3)$
Vậy phương trình đường cao $AA’$ có điểm đi qua $A(4, 4)$ và nhận véc tơ $(0, 3)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=4 \\ y=4+3t\end{array}\right.$
Phương trình đường cao $BB’$
Dễ thấy véc tơ $\overrightarrow{CA}=(-2 ,2)$ là véc tơ chỉ phương của đường thẳng $CA$
Suy ra véc tơ chỉ phương của đường cao $BB’$ là $(-2, -2)$
Vậy phương trình đường cao $BB’$ có điểm đi qua $B(3, 2)$ và nhận véc tơ $(-2, -2)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=3-2t \\ y=2-2t\end{array}\right.$
Phương trình đường cao $CC’$
Dễ thấy véc tơ $\overrightarrow{AB}=(-1 ,-2)$ là véc tơ chỉ phương của đường thẳng $AB$
Suy ra véc tơ chỉ phương của đường cao $CC’$ là $(2, -1)$
Vậy phương trình đường cao $CC’$ có điểm đi qua $C(6, 2)$ và nhận véc tơ $(2, -1)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=6+2t \\ y=2-t\end{array}\right.$
#4. Lời Kết
Đến đây chúng ta đã tìm hiểu xong cách viết phương trình đường cao trong tam giác rồi ha.
Đây cũng là phương trình đường thẳng đồng quy trong tam giác cuối cùng mà mình hướng dẫn cho các bạn.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Nếu muốn tìm hiểu thêm cách viết các phương trình đồng quy khác, bạn hãy nháy chuột vào liên kết tương ứng bạn nhé:
- Cách viết phương trình đường trung tuyến
- Cách viết phương trình đường phân giác
- Cách viết phương trình đường trung trực
Hi vọng những thông tin trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
