Cách tính độ dài đường cao trong hình học giải tích

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính độ dài ba đường cao của một tam giác bất kỳ trong hình học giải tích.

Để thuận tiện cho các bạn trong việc tìm hiểu kiến thức mới/ôn lại kiến thức cũ thì mình sẽ cố gắng trình bày chi tiết nhất có thể, bắt đầu với các bước tính độ dài đường cao và kết thúc bằng việc giải một ví dụ minh họa tương ứng.

#1. Cách bước tính độ dài đường cao trong tam giác

Cho tam giác $ABC$ có $A(x_a, y_a), B(x_b, y_b), C(x_c, y_c)$, tính độ dài các đường cao của tam giác $ABC$

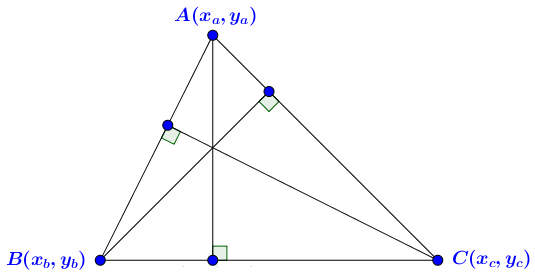
Gọi $AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$

+) Tính độ dài đường cao $(AA’)$

Bước 1. Viết phương trình đường cao $(AA’)$

Giả sử phương trình đường cao $(AA’): A_1x+B_1y+C_1=0$

Bước 2. Viết phương trình đường thẳng $(BC)$

Giả sử phương trình đường thẳng $(BC): A_2x+B_2y+C_2=0$

Bước 3. Tọa độ của $A’$ là nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_1x+B_1y+C_1=0 \\ A_2x+B_2y+C_2=0\end{array}\right.$

Giả sử tọa độ của $A’(x_a’, y_a’)$

Bước 4. Khoảng cách $AA’$ chính là độ dài của đường cao $(AA’)$

$AA’=\sqrt{(x_a’-x_a)^2+(y_a’-y_a)^2}$

+) Tính độ dài đường cao $(BB)’$

Bước 1. Viết phương trình đường cao $(BB)’$

Giả sử phương trình đường cao $(BB’): A_3x+B_3y+C_3=0$

Bước 2. Viết phương trình đường thẳng $(CA)$

Giả sử phương trình đường thẳng $(CA): A_4x+B_4y+C_4=0$

Bước 3. Tọa độ của $B’$ là nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_3x+B_3y+C_3=0 \\ A_4x+B_4y+C_4=0\end{array}\right.$

Giả sử tọa độ của $B’(x_b’, y_b’)$

Bước 4. Khoảng cách $BB’$ chính là độ dài của đường cao $(BB’)$

$BB’=\sqrt{(x_b’-x_b)^2+(y_b’-y_b)^2}$

+) Tính độ dài đường cao $(CC’)$

Bước 1. Viết phương trình đường cao $(CC’)$

Giả sử phương trình đường cao $(CC’): A_5x+B_5y+C_5=0$

Bước 2. Viết phương trình đường thẳng $(AB)$

Giả sử phương trình đường thẳng $(AB): A_6x+B_6y+C_6=0$

Bước 3. Tọa độ của $C’$ là nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_5x+B_5y+C_5=0 \\ A_6x+B_6y+C_6=0\end{array}\right.$

Giả sử tọa độ của $C’(x_c’, y_c’)$

Bước 4. Khoảng cách $CC’$ chính là độ dài của đường cao $(CC’)$

$CC’=\sqrt{(x_c’-x_c)^2+(y_c’-y_c)^2}$

#2. Bài tập ví dụ

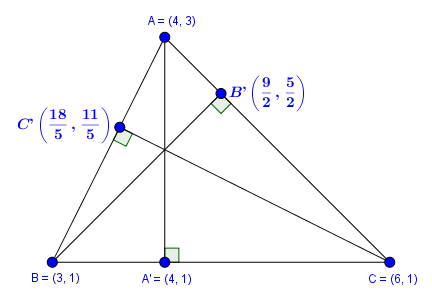
Cho tam giác $ABC$ có $A(4, 3), B(3, 1), C(6, 1)$, tính độ dài các đường cao của tam giác $ABC$

Cách 1. Áp dụng phương pháp hình học giải tích

Gọi $AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$

+) Độ dài đường cao $AA’$

Dễ thấy phương trình đường cao $AA’$ là $x-4=0$

Xem thêm:
Cách viết phương trình đường cao

Dễ thấy véc tơ $\overrightarrow{BC}=(3, 0)$

Phương trình đường thẳng $(BC)$ đi qua điểm $B(3 ,1)$ và nhận véc tơ $\overrightarrow{BC}=(3, 0)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l} x=3+3t \\ y=1\end{array}\right. \Leftrightarrow y-1=0$

Giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x-4=0 \\ y-1=0 \end{array}\right.$ ta được nghiệm là $(4, 1)$

Suy ra $A’(4, 1)$

Vậy độ dài đường cao $AA’=\sqrt{(4-4)^2+(1-3)^2}=2$

+) Độ dài đường cao $BB’$

Dễ thấy phương trình đường cao $BB’$ là $x-y-2=0$

Dễ thấy véc tơ $\overrightarrow{CA}=(-2, 2)$

Phương trình đường thẳng $(CA)$ đi qua điểm $C(6 ,1)$ và nhận véc tơ $\overrightarrow{CA}=(-2, 2)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l} x=6-2t \\ y=1+2t\end{array}\right. \Leftrightarrow -x-y+7=0$

Giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x-y-2=0 \\ -x-y+7=0 \end{array}\right.$ ta được nghiệm là $\left(\frac{9}{2}, \frac{5}{2}\right)$

Suy ra $B’\left(\frac{9}{2}, \frac{5}{2}\right)$

Vậy độ dài đường cao $BB’=\sqrt{\left(\frac{9}{2}-3\right)^2+\left(\frac{5}{2}-1\right)^2}=\frac{3\sqrt{2}}{2}$

+) Độ dài đường cao $CC’$

Dễ thấy phương trình đường cao $CC’$ là $x+2y-8=0$

Dễ thấy véc tơ $\overrightarrow{AB}=(-1, -2)$

Phương trình đường thẳng $(AB)$ đi qua điểm $A(4 ,3)$ và nhận véc tơ $\overrightarrow{AB}=(-1, -2)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l} x=4-t \\ y=3-2t\end{array}\right. \Leftrightarrow 2x-y-5=0$

Giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} x+2y-8=0 \\ 2x-y-5=0 \end{array}\right.$ ta được nghiệm là $\left(\frac{18}{5}, \frac{11}{5}\right)$

Suy ra $C’\left(\frac{18}{5}, \frac{11}{5}\right)$

Vậy độ dài đường cao $CC’=\sqrt{\left(\frac{18}{5}-6\right)^2+\left(\frac{11}{5}-1\right)^2}=\frac{6\sqrt{5}}{5}$

Cách 2. Tính độ dài ba cạnh $BC, CA, AB$ rồi áp dụng cách tính độ dài đường cao trong hình học sơ cấp

Lời giải chi tiết của cách này xin dành cho các bạn

Thông thường, nếu tính độ dài đường cao của hình học giải tích bằng cách tính của hình học sơ cấp thì số sẽ khá khó khăn, tính toán phức tạp.

Vậy nên, nếu bạn chọn cách này thì bạn nên chuẩn bị máy tính CASIO fx-580VN X hoặc các dòng máy tính tương đương, sẽ rất có ích

#3. Lời kết

Việc tính độ dài đường cao của tam giác trong hình học giải tích có phần đơn giản hơn nếu so với hình học sơ cấp

Thật vậy:

• Trong hình học sơ cấp tuy vẫn có công thức chung cho phép chúng ta tính độ dài đường cao của tam giác bất kỳ, thế nhưng công thức này khá phức tạp và khó nhớ.
• Còn trong hình học giải tích thì chỉ cần tìm được giao điểm, áp dụng công thức tính khoảng cách giữa hai điểm là xong, đơn giản và dễ nhớ hơn khá nhiều.

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn