Cách tìm trọng tâm của tam giác

Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn với các bạn cách tìm trọng tâm của một tam giác bất kỳ.

Không giống như hầu hết các bài viết hiện có trên Internet, trong bài viết này mình sẽ hướng dẫn cho cách tìm trong cả hai trường hợp là hình học sơ cấp và hình học giải tích

Cụ thể thì:

• Nếu là bài toán hình học sơ cấp, chúng ta sẽ tìm được vị trí của trọng tâm.
• Nếu là bài toán hình học giải tích, chúng ta sẽ tìm được tọa độ của trọng tâm.

#1. Trọng tâm của tam giác là gì?

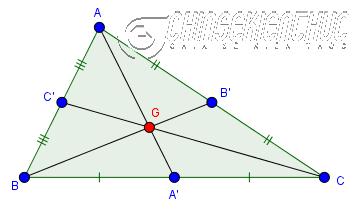
Ba đường trung tuyến của tam giác đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

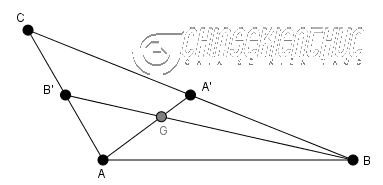
Ví dụ như hình bên trên, điểm $G$ là giao điểm của ba đường trung tuyến $AA’, BB’, CC’$ nên $G$ là trọng tâm của tam giác $ABC$

Chú ý:

Nếu $G$ là trọng tâm của tam giác $ABC$ thì chúng ta sẽ có:

• $AG=\frac{2}{3}AA’$
• $BG=\frac{2}{3}BB’$
• $CG=\frac{2}{3}CC’$

#2. Các bước tìm trọng tâm của tam giác (hình học sơ cấp)

Bản chất của việc tìm trọng tâm của tam giác trong hình học sơ cấp chính là vẽ được điểm $G$

Công cụ cần chuyển bị trước khi thực hiện:

1. Thước thẳng
2. Compa

Các bước thực hiện như sau:

#3. Các bước tìm trọng của tâm tam giác (hình học giải tích)

Trong hầu hết các trường hợp thì Cách 1 là cách tối ưu nhất, còn Cách 2 mang tính chất tham khảo thêm là chính nha các bạn.

Cách #1. Dựa vào công thức riêng

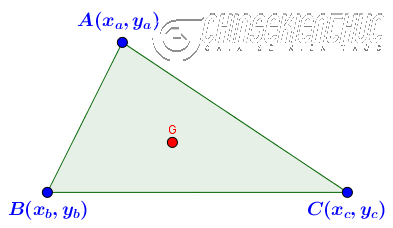
Cho tam giác $ABC$ có $A(x_a, y_a), B(x_b, y_b), C(x_c, y_c)$, tìm tọa độ trọng tâm $G$ của tam giác $ABC$

Trọng tâm $G$ của tam giác $ABC$ sẽ được tính theo công thức: $G\left(\frac{x_a+x_b+x_c}{3}, \frac{y_a+y_b+y_c}{3}\right)$

Cách #2. Dựa vào định nghĩa

Cho tam giác $ABC$ có $A(x_a, y_a), B(x_b, y_b), C(x_c, y_c)$, tìm tọa độ trọng tâm $G$ của tam giác $ABC$

Bước 1. Tìm tọa độ trung điểm $A’$ của cạnh $BC$ và trung điểm $B’$ của cạnh $CA$

Bước 2. Viết phương trình đường trung tuyến $(AA’)$

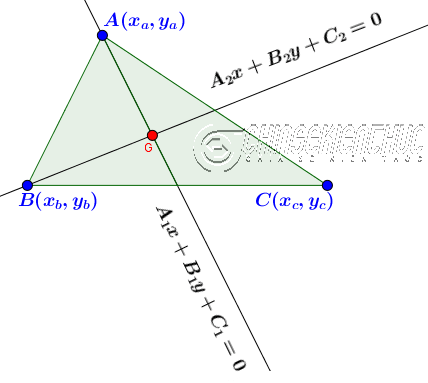
Giả sử phương trình đường trung tuyến $(AA’)$ là $A_1x+B_1y+C_1=0$

Bước 3. Viết phương trình đường trung tuyến $(BB’)$

Giả sử phương trình đường trung tuyến $(BB’)$ là $A_2x+B_2y+C_2=0$

Bước 4. Nghiệm của hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l} A_1x+B_1y+C_1=0 \\ A_2x+B_2y+C_2=0\end{array}\right.$ là tọa độ của trọng tâm $G$

#4. Bài tập ví dụ

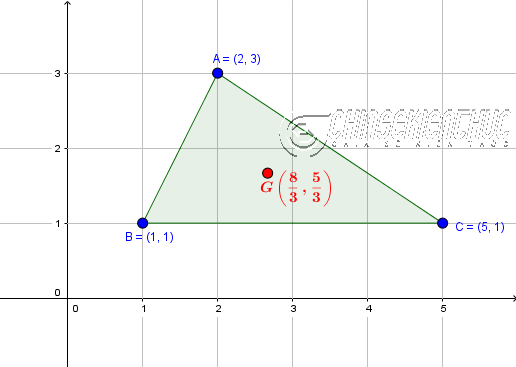
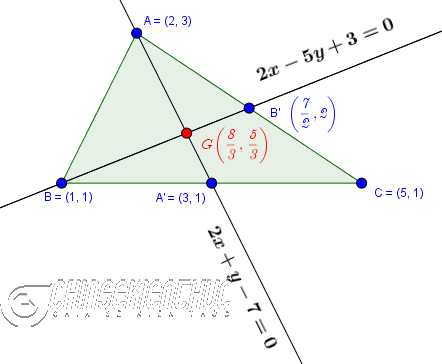
Ví dụ 1. Cho tam giác $ABC$ có $A(2, 3), B(1, 1), C(5, 1)$, tìm tọa độ trong tâm $G$ của tam giác $ABC$

Cách #1. Dựa vào công thức riêng

Tọa độ trọng tâm $G$ của tam giác $ABC$ là $\left(\frac{2+1+5}{3},\frac{3+1+1}{3}\right)=\left(\frac{8}{3},\frac{5}{3}\right)$

Cách #2. Dựa vào định nghĩa

Gọi $A’, B’$ lần lượt là trung điểm của các cạnh $BC, CA$

$A’(\frac{1+5}{2}, \frac{1+1}{2})=(3, 1)$

$B’(\frac{5+2}{2}, \frac{1+3}{2})=(\frac{7}{2}, 2)$

Dễ thấy véc tơ $\overrightarrow{AA’}=(1, -2)$

Phương trình đường trung tuyến đi qua điểm $A(2, 3)$ và nhận véc tơ $\overrightarrow{AA’}=(1, -2)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=2+t \\ y=3-2t\end{array}\right.$ hay $2x+y-7=0$

Dễ thấy véc tơ $\overrightarrow{BB’}=(\frac{5}{2}, 1)$

Phương trình đường trung tuyến đi qua điểm $B(1, 1)$ và nhận véc tơ $\overrightarrow{BB’}=(\frac{5}{2}, 1)$ làm véc tơ chỉ phương là $\left\{\begin{array}{l}x=1+\frac{5}{2}t \\ y=1+t\end{array}\right.$ hay $2x-5y+3=0$

Giải hệ hai phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}2x+y-7=0 \\ 2x-5y+3=0\end{array}\right.$ $(*)$

$(*) \Leftrightarrow \left\{\begin{array}{l}2x+y-7=0 \\ 6y-10=0\end{array}\right.$

$(*) \Leftrightarrow \left\{\begin{array}{l}2x+y-7=0 \\ y=\frac{5}{3}\end{array}\right.$

$(*) \Leftrightarrow \left\{\begin{array}{l}2x+\frac{5}{3}-7=0 \\ y=\frac{5}{3}\end{array}\right.$

$(*) \Leftrightarrow \left\{\begin{array}{l}x=\frac{8}{3} \\ y=\frac{5}{3}\end{array}\right.$

Vậy trọng tâm $G$ của tam giác $ABC$ là $\left(\frac{8}{3}, \frac{5}{3}\right)$

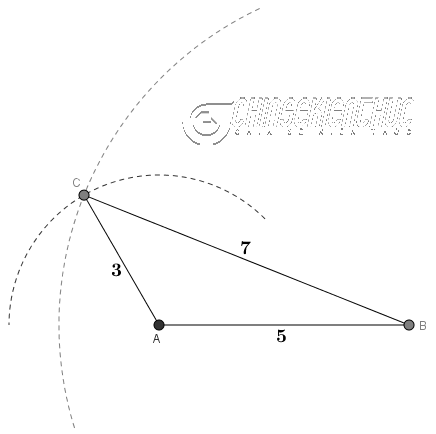
Ví dụ 2. Cho tam giác $ABC$ có $BC=7, CA=3, AB=5$, vẽ trọng tâm $G$ của tam giác $ABC$

Bước 1. Vẽ tam giác $ABC$

Xem thêm:
Cách vẽ một tam giác bất kỳ

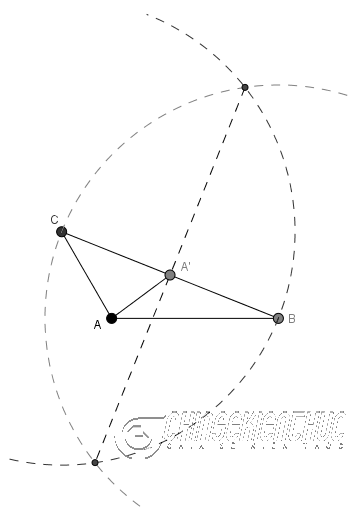
Bước 2. Vẽ trung điểm $A’$ của cạnh $BC$ => vẽ đường trung tuyến $AA’$

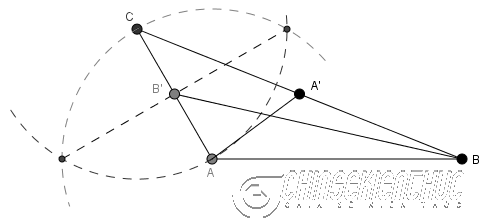
Bước 3. Vẽ trung điểm $B’$ của cạnh $CA$ => vẽ đường trung tuyến $BB’$

Bước 4. Vẽ giao điểm $G$ của đường trung tuyến $AA’$ và đường trung tuyến $BB’$

#5. Lời kết

Okay, về cơ bản thì cách tìm trọng tâm của tam giác cũng không có gì khó khăn cả.

Tùy thuộc vào bài toán được cho trong hình học sơ cấp hay hình học giải tích mà chúng ta sẽ cân nhắc, lựa chọn phương pháp sao cho phù hợp.

Riêng trong trường hợp đặc biệt, nếu tam giác cần tìm trọng tâm là tam giác vuông thì trọng tâm chính là trung điểm của cạnh huyền. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn