Cách vẽ một tam giác bất kỳ (3 trường hợp, có ví dụ)

Về lý thuyết thì chúng ta luôn vẽ được một tam giác bất kỳ nếu biết được ít nhất ba yếu tố (độ dài của cạnh, độ lớn của góc) với điều kiện yếu tố góc không quá hai.

Về bài tập thực hành thì chúng ta cần phải biết cách vẽ, cũng như các bước vẽ một tam giác bất kỳ. Okay, sau đây là 3 trường hợp mà mình đang muốn đề cập đến:

#1. Vẽ tam giác khi biết độ dài ba cạnh

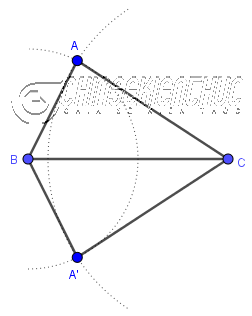
Vẽ tam giác ABC biết AB = c, BC = a, CA = b

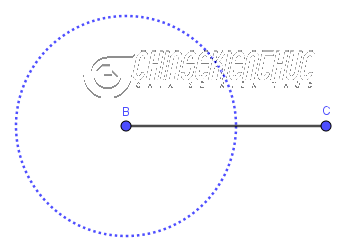
Bước 1. Vẽ đoạn thẳng BC = a

Bước 2. Vẽ đường tròn tâm B bán kính c

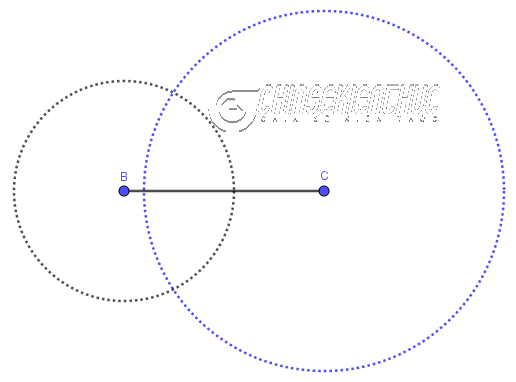
Bước 3. Vẽ đường tròn tâm C bán kính b

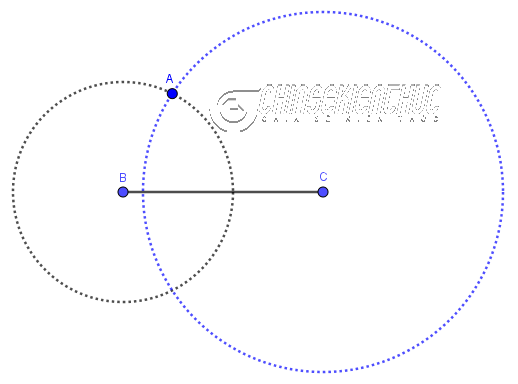
Bước 4. Vẽ giao điểm A của hai đường tròn

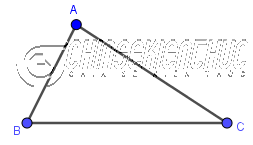
Bước 5. Vẽ cạnh BA, CA

Ví dụ 1: Vẽ tam giác ABC biết AB = 2.2 cm; BC = 4 cm; CA = 3.6 cm

Bước 1. Vẽ đoạn thẳng BC = 4 cm

Bước 2. Vẽ đường tròn tâm B bán kính 2.2 cm

Bước 3. Vẽ đường tròn tâm C bán kính 3.6 cm

Bước 4. Vẽ giao điểm A của hai đường tròn

Bước 5. Vẽ cạnh BA, CA

Nhận xét về cách vẽ:

• Bạn có thể vẽ cung tròn phù hợp (cắt nhau) thay vì phải vẽ cả đường tròn
• Đường tròn / cung tròn nên được vẽ bằng bút chì
• Dễ thấy hai đường tròn có hai giao điểm nên sẽ vẽ được hai tam giác thỏa mãn điều kiện

#2. Vẽ tam giác khi biết độ dài hai cạnh và độ lớn của góc xen giữa

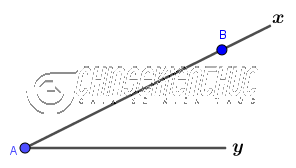
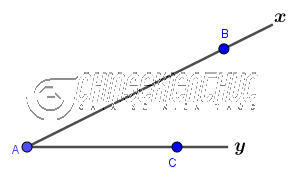
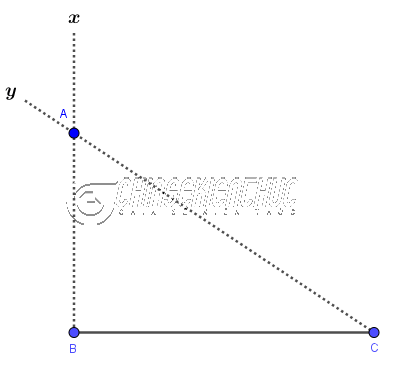
Vẽ tam giác ABC biết $AB=c, AC=b, \hat{A}=\alpha$

Bước 1. Vẽ $\widehat{xAy}=\alpha$

Bước 2. Trên tia Ax vẽ đoạn thẳng AB=c

Bước 3. Trên tia Ay vẽ đoạn thẳng AC=b

Bước 4. Vẽ đoạn thẳng BC

Ví dụ 2: Vẽ tam giác ABC biết $AB=4.4~cm; AC=3~cm, \hat{A}=26.5^o$

Bước 1. Vẽ $\widehat{xAy}=26.5^o$

Bước 2. Trên tia Ax vẽ đoạn thẳng AB = 4.4 cm

Bước 3. Trên tia Ay vẽ đoạn thẳng AC=3 cm

Bước 4. Vẽ đoạn thẳng BC

Nhận xét cách vẽ:

• $\widehat{A}$ được vẽ bằng thước đo góc
• AB, AC được vẽ bằng thước thẳng có chia vạch hoặc Compa với đường tròn / cung tròn có bán kính lần lượt là c, a

#3. Vẽ tam giác khi biết độ dài một cạnh và độ lớn của hai góc kề

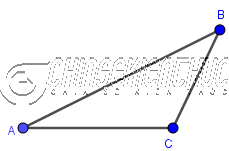
Vẽ tam giác ABC biết $BC=a, \hat{B}=\beta, \hat{C}=\gamma$

Bước 1. Vẽ cạnh BC = a

Bước 2. Vẽ tia Bx sao cho $\widehat{xBC}=\beta$

Bước 3. Vẽ tia Cy sao cho $\widehat{yCB}=\gamma$

Bước 4. Vẽ giao điểm A của hai tia Bx, Cy

Bước 5. Vẽ cạnh BA, CA

Chú ý: Tia Bx và Cy phải cùng nằm trên một nửa mặt phẳng có bờ là cạnh BC

Ví dụ 3: Vẽ tam giác ABC biết $BC=6~cm, \hat{B}=90^o, \hat{C}=33.6^o$

Bước 1. Vẽ cạnh BC=6 cm

Bước 2. Vẽ tia Bx sao cho $\widehat{xBC}=90^o$

Bước 3. Vẽ tia Cy sao cho $\widehat{yCB}=33.6^o$

Bước 4. Vẽ giao điểm A của hai tia Bx, Cy

Bước 5. Vẽ cạnh BA, CA

Nhận xét về các vẽ: Trong một số trường hợp ta cần kéo dài tia Bx và Cy thì mới có thể vẽ được giao điểm

#4. Lời kết

Vâng, như vậy là mình đã hướng dẫn xong cho các bạn cách vẽ một tam giác bất kỳ rồi nhé. Nói tóm lại:

Muốn vẽ được tam giác …

• Điều kiện 1: Tam giác phải tồn tại (tức tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại), vẽ tam giác có độ dài ba cạnh lần lượt là 2, 3, 5 là không khả thi vì tam giác này không tồn tại.
• Điều kiện 2: Được cung cấp 3 yếu tố của tam giác, vẽ tam giác khi biết độ lớn ba góc là không khả khi (không sư phạm) vì có thể vẽ được vô số tam giác.
• Điều kiện 3: Biết cách vẽ tam giác

Nếu bạn là học sinh thì bạn chỉ cần biết cách vẽ tam giác là được, Điều kiện 1 và 2 giáo viên sẽ lo cho bạn.

Mình xin nói thêm là trong 3 trường hợp trên chỉ có Trường hợp 1 là bài toán dựng hình, vì chỉ sử dụng hai công cụ là thước thẳng và Compa

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com