Cách tính đường cao trong tam giác vuông, cân, đều…

Khi nhắc đến đường cao thì mặc định chúng ta sẽ hiểu là đường cao trong tam giác. Và người ta định nghĩa đường cao là đường thẳng đi qua đỉnh và vuông góc với cạnh đối diện.

Theo định nghĩa bên trên thì đường cao là đường thẳng, mà đường thẳng thì có độ dài vô hạn. Tuy nhiên, đường thẳng này bị giới hạn bởi đỉnh và cạnh đối diện nên chúng ta mới có thể tính được độ dài.

Vậy nên độ dài đường cao phải được hiểu như trên để tránh bị tẩu hỏa nhập ma ^^

#1. Nhắc lại định nghĩa đường cao

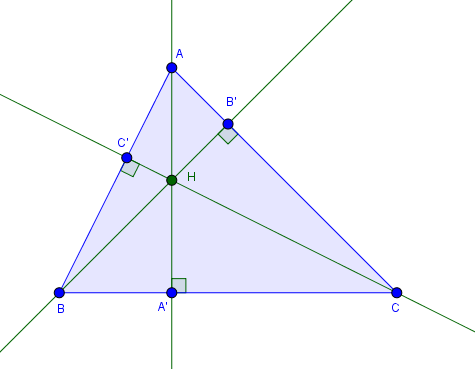
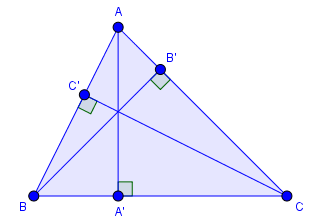
Đường cao trong tam giác là đường thẳng đi qua một đỉnh và vuông góc với cạnh đối diện.

Tam giác nào cũng có ba đường cao, ba đường cao này đồng quy tại một điểm, điểm đồng quy được gọi là trực tâm.

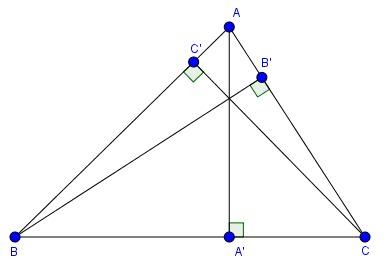
$AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$ của tam giác $ABC$

$H$ là trực tâm của tam giác $ABC$

#2. Cách tính độ dài đường cao trong tam giác thường

Công thức tính độ dài đường cao cao trong tam giác thường là công thức tổng quát để tính đường cao, có nghĩa là bạn có thể áp dụng công thức này để tính độ dài đường cao trong các tam giác đặc biệt.

Cho tam giác $ABC$ có $BC=a, CA=b, AB=c$ tính độ dài các đường cao của tam giác $ABC$

Gọi $AA’, BB’, CC’$ lần lượt là ba đường cao xuất phát từ ba đỉnh $A, B, C$

Theo công thức Hê rông ta có $S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$ với $p=\frac{a+b+c}{2}$

Mặc khác ta lại có $S_{ABC}=\frac{1}{2}aAA’$

Suy ra $\frac{1}{2}aAA’=\sqrt{p(p-a)(p-b)(p-c)}$ hay $AA’=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{a}$

Lập luận hoàn toàn tương tự ta cũng có $BB’=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{b}$, $CC’=\frac{2\sqrt{p(p-a)(p-b)(p-c)}}{c}$

#3. Công thức tính độ dài đường cao (tam giác vuông, cân, vuông cân, đều)

Dưới đây là công thức tính độ dài đường cao trong những tam giác đặc biệt, tam giác càng đặc biệt thì công thức tính càng đơn giản.

3.1. Tính độ dài đường cao của tam giác cân

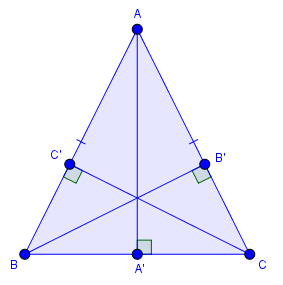
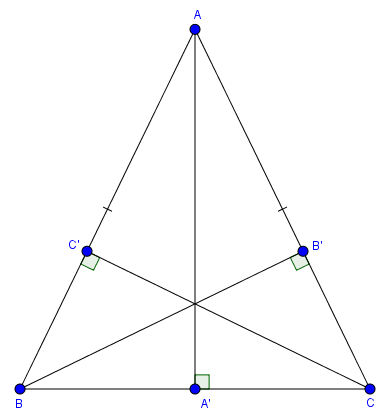
Cho tam giác $ABC$ cân tại $A$ có $BC=a, CA=AB=b, AA’, BB’, CC’$ là lần lượt là ba đường cao xuất phát từ đỉnh ba đỉnh $A, B, C$

Tính độ dài đường cao $AA’$

Áp dụng định lí Pytago vào tam giác vuông $AA’C$ ta có $AA’^2=AC^2-A’C^2=b^2-\frac{a^2}{4}$

Suy ra $AA’=\sqrt{b^2-\frac{a^2}{4}}=\frac{1}{2}\sqrt{4b^2-a^2}$

Tính độ dài đường cao $BB’$ và $CC’$

Theo công thức Hê rông ta có $S_{ABC}=\sqrt{\frac{a+2b}{2}\left(\frac{a+2b}{2}-a\right)\left(\frac{a+2b}{2}-b\right)\left(\frac{a+2b}{2}-b\right)}=\frac{1}{4}a\sqrt{4b^2-a^2}$

Mặc khác ta lại có $S_{ABC}=\frac{1}{2}bBB’$

Suy ra $\frac{1}{2}bBB’=\frac{1}{4}a\sqrt{4b^2-a^2} \Leftrightarrow BB’=\frac{a\sqrt{4b^2-a^2}}{2b}$

Suy ra $CC’=\frac{a\sqrt{4b^2-a^2}}{2b}$

3.2. Tính độ dài đường cao của tam giác vuông

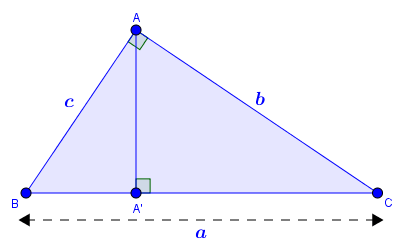
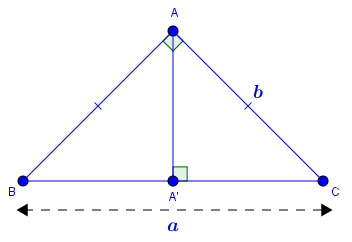
Cho tam giác $ABC$ vuông tại $A$ có $BC=a, CA=b, AB=c, AA’$ là đường cao xuất phát từ đỉnh $A$

Dễ thấy …

• Đường cao xuất phát từ đỉnh $B$ là chính là cạnh $BA$
• Đường cao xuất phát từ đỉnh $C$ chính là cạnh $CA$

Suy ra đường cao xuất phát từ đỉnh $B$ có độ dài là $c$ và đỉnh $C$ có độ dài là $b$

Tính độ dài đường cao $AA’$

Có nhiều công thức để tính độ dài đường cao trong tam giác vuông, một trong những có thức dễ nhớ, dễ sử dụng nhất là …

$\frac{1}{AA’^2}=\frac{1}{b^2}+\frac{1}{c^2}$

Suy ra $AA’=\frac{bc}{\sqrt{b^2+c^2}}$ $(*)$

3.3. Tính độ dài đường cao của tam giác vuông cân

Cho tam giác $ABC$ vuông cân tại $A$, có $BC=a, CA=AB=b, AA’$ là đường cao xuất phát từ đỉnh $A$

Dễ thấy …

• Đường cao xuất phát từ đỉnh $B$ chính là cạnh $BA$
• Đường cao xuất phát từ đỉnh $C$ chính là cạnh $CA$

Suy ra đường cao xuất phát từ đỉnh $B$ và đỉnh $C$ có độ dài là $b$

Tính độ dài đường cao $AA’$

Dễ thấy tam giác $AA’C$ là tam giác vuông cân tại $A’$

Suy ra $AA’=\frac{BC}{2}=\frac{a}{2}$

3.4. Tính độ dài đường cao của tam giác đều

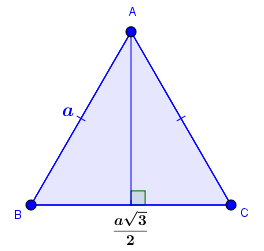
Cho tam giác đều $ABC$ có $BC=CA=AB=a$, tính độ dài ba đường cao của tam giác $ABC$

Độ dài ba đường cao trong tam giác đều $ABC$ luôn bằng $\frac{a\sqrt{3}}{2}$

#4. Bài tập ví dụ

Ví dụ 1. Cho tam giác $ABC$ có $BC=7, CA=5, AB=6$, tính độ dài các đường cao $AA’, BB’, CC’$

Nửa chu vi của tam giác $ABC$ là $\frac{7+5+6}{2}=9$

Suy ra diện tích tam giác $ABC$ là $\sqrt{9(9-7)(9-5)(9-6)}=6\sqrt{6}$

Mặc khác $\frac{1}{2}BC.AA’=6\sqrt{6} \Leftrightarrow \frac{1}{2}.7.AA’=6\sqrt{6} \Leftrightarrow AA’=\frac{12\sqrt{6}}{7}$

Lập luận tương tự ta có …

• $\frac{1}{2}CA.BB’=6\sqrt{6} \Leftrightarrow \frac{1}{2}.5.BB’=6\sqrt{6} \Leftrightarrow BB’=\frac{12\sqrt{6}}{5}$
• $\frac{1}{2}AB.CC’=6\sqrt{6} \Leftrightarrow \frac{1}{2}.6.CC’=6\sqrt{6} \Leftrightarrow CC’=2\sqrt{6}$

Vậy độ dài ba đường cao trong tam giác $ABC$ lần lượt là $\frac{12\sqrt{6}}{7}, \frac{12\sqrt{6}}{5}, 2\sqrt{6}$

Ví dụ 2. Cho tam giác $ABC$ cân tại $A$ có $BC=7, CA=AB=8$, tính độ dài các đường cao $AA’, BB’, CC’$

Áp dụng định lý Pytago vào tam giác vuông $AA’C$ ta được $AA’^2=AC^2-A’C^2=8^2-\left(\frac{7}{2}\right)^2=\frac{207}{4}$

Suy ra $AA’=\frac{3\sqrt{23}}{2}$

Áp dụng công thức $BB’=\frac{a\sqrt{4b^2-a^2}}{2b}$ vào tam giác $ABC$ ta được $BB’=\frac{7\sqrt{4.8^2-7^2}}{2.8}=\frac{21\sqrt{23}}{16}$

Suy ra $CC’=\frac{21\sqrt{23}}{16}$

Vậy độ dài ba đường cao của tam giác $ABC$ lần lượt bằng $\frac{3\sqrt{23}}{2}, \frac{21\sqrt{23}}{16}, \frac{21\sqrt{23}}{16}$

#5. Lời kết

Vâng, như vậy là qua bài viết này thì bạn đã biết cách tính đường cao trong tam giác rồi đúng không ?!

Công thức tính độ dài đường cao tổng quát nhất chính là công thức đầu tiên, tức công thức tính độ dài đường cao trong tam giác thường.

Mọi tam giác đặc biệt như tam giác cân, tam giác vuông, tam giác vuông cân, tam giác đều đều có thể sử dụng được công thức này.

Tuy nhiên, nếu bạn nhớ được hết các công thức đặc biệt thì quá tốt, khi giả thuyết cho tam giác nào ta chỉ việc áp dụng công thức dành riêng cho tam giác đó, vừa nhanh, lại vừa dễ dàng khi tính toán.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Công thức tính độ dài đường phân giác
• Hướng dẫn 2 cách tính độ dài đường trung tuyến
• Cách tính diện tích đa giác đều (ngũ giác đều, lục giác đều…)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn