Định lý Pytago thuận, định lý Pytago đảo và bài tập ví dụ !

Hướng dẫn cách sử dụng định lý Pytago để giải bài tập..

Xin chào tất cả các bạn, bài viết này chúng ta sẽ cùng nhau tìm hiểu về định lý Pytago !

Đây là một định lý hình học rất quen thuộc, có rất nhiều cách chứng minh và cũng là định lý duy nhất tính đến thời điểm hiện tại được chứng minh bởi một vị Tổng thống của Hoa Kì.

#1. Định lý Pytago thuận

Trong một tam giác vuông, ta luôn có bình phương của độ dài cạnh huyền bằng tổng bình phương của độ dài hai cạnh góc vuông.

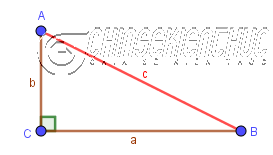
Công thức: $c^2=a^2+b^2$

• c là độ dài cạnh huyền.
• a, b là độ dài hai cạnh góc vuông.

Định lý Pytago thuận sẽ biểu diễn mối quan hệ giữa các cạnh trong tam giác, nhờ vào mối quan trên mà chúng ta có thể áp dụng định lý để:

• Tìm độ dài cạnh huyền khi biết độ dài hai cạnh góc vuông.
• Tìm độ dài cạnh góc vuông khi biết độ dài cạnh huyền và cạnh góc vuông còn lại.

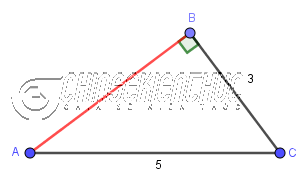
Ví dụ 1: Cho tam giác ABC có góc ABC bằng 90^o, AC=5, BC=3. Tính độ dài cạnh BA

Lời Giải:

Áp dụng định lý Pytago $c^2=a^2+b^2$ vào tam giác vuông ABC ta được $5^2=BA^2+3^2$

=> $BA=\sqrt{5^2-3^2}=\sqrt{25-9}=\sqrt{16}=4$

Vậy độ dài cạnh BA bằng 4 ĐVĐD

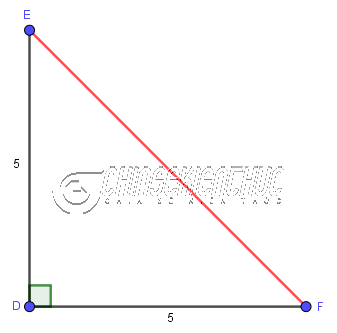
Ví dụ 2: Cho tam giác DEF (vuông tại góc EDF) có DE=5, DF=5. Tính đó dài cạnh EF.

Lời Giải:

Phương pháp 1: Sử dụng định lý Pytago

Áp dụng định lí Pytago $c^2=a^2+b^2$ vào tam giác vuông DEF ta được $EF^2=5^2+5^2$

=> $EF=\sqrt{5^2+5^2}=\sqrt{25+25}=\sqrt{50}=5\sqrt{2}$

Vậy độ dài cạnh EF bằng $5\sqrt{2}$ ĐVĐD

Phương pháp 2:

Vì tam giác DEF là tam giác vuông cân và độ dài cạnh cần tìm là cạnh huyền nên độ dài cạnh huyền sẽ bằng tích của căn 2 và độ dài cạnh góc vuông.

=> Độ dài cạnh huyền bằng $\sqrt{2} \times 5$

Vậy độ dài cạnh EF bằng $5\sqrt{2}$ ĐVĐD

#2 Định lý Pytago đảo

Nếu một tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại thì tam giác đó là tam giác vuông.

Công thức: $\triangle ABC, BC^2=AB^2+AC^2 \Rightarrow \widehat{BAC}=90^o$

Định lý Pytago đảo là một trong những cách đơn giản nhất giúp chúng ta chứng minh hoặc đơn giản hơn là kiểm tra tam giác đã cho có phải tam giác vuông hay không.

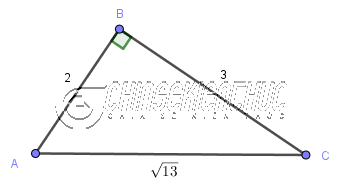
Ví dụ 3: Cho tam giác ABC có $AB=2, BC=3, CA=\sqrt{13}$

Câu Hỏi:

1. Tam giác ABC có phải tam giác vuông hay không?
2. Nếu vuông thì vuông ở góc nào?
3. Vẽ hình minh họa

Dễ thấy cạnh CA có độ dài lớn nhất, nếu ta có đẳng thức $CA^2=AB^2+BC^2$ thì tam giác ABC là tam giác vuông

Lời Giải:

a) Ta có:

• $CA^2=\sqrt{13}^2=13$
• $AB^2+BC^2=2^2+3^2=4+9=13$

Suy ra $CA^2=AB^2+BC^2$

=> Theo định lí Pytago đảo thì tam giác ABC là tam giác vuông.

b) Tam giác ABC vuông tại B

c)

#3. Cách chứng minh định lý Pytago

Như mình có nói ở đầu bài viết, định lý này là một trong những định lý có nhiều cách chứng minh nhất.

Nhiều tới nỗi có thể viết thành một quyển sách 😀

Thật vậy, trong quyển The Pythagorean Proposition đã giới thiệu 370 cách chứng minh khác nhau. Dưới đây là một trong những cách chứng minh lâu đời nhất và đơn giản nhất:

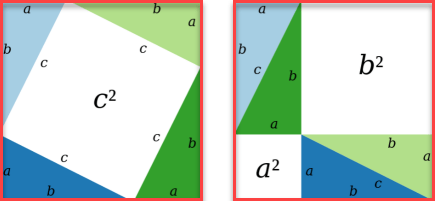
• Hai hình vuông lớn có diện tích bằng nhau.
• Mỗi hình vuông lớn chứa bốn tam giác vuông bằng nhau.
• Tam giác vuông trong hình vuông lớn này bằng tam giác vuông trong hình vuông lớn kia.
• Mỗi hình vuông lớn có cách sắp xếp bốn tam giác vuông khác nhau (xem hình)

Suy ra diện tích miền màu trắng bên trong mỗi hình vuông lớn bằng nhau.

=> Điều phải chứng minh $c^2=a^2+b^2$

Một số phương pháp chứng minh khác (mình chỉ liệt kê tên mà thôi).

1. Sử dụng các tam giác đồng dạng
2. Phương pháp Ơ-clít
3. Phương pháp chia ra và ráp lại
4. Phương pháp Albert Einstein
5. Phương pháp đại số
6. Sử dụng vi tích phân

Về định lí đảo thì bạn có thể chứng minh dựa vào định lý COS (Law of cosines) hay còn gọi là định lý hàm COS, định lý Côsin.

#4. Lời kết

Okay, trên đây là định lý Pytago thuận và định lý Pytago đảo và một số ví dụ để các bạn dễ hình dung hơn.

Định lý Pytago có một hạn chế là chỉ có thể áp dụng được với tam giác vuông, trường hợp là một tam giác bất kì thì bạn cần áp dụng định lý hàm COS để chứng minh.

Đó là đôi lời gợi ý của mình, giúp bạn có hướng tham khảo thêm, mở rộng kiến thức. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Làm thế nào để vẽ đường tròn ngoại tiếp tam giác?
• Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com