Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

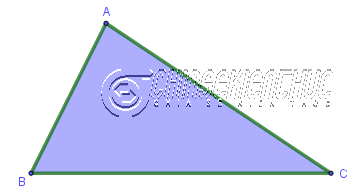
Có rất nhiều cách để định nghĩa tam giác ABC, dưới đây là một trong những cách dễ hiểu nhất mà mình muốn chia sẻ với các bạn.

• Tam giác ABC là một hình bao gồm ba đoạn thẳng AB, BC, CA (ba điểm A, B, C không thẳng hàng).
• Tam giác ABC được kí hiệu là $\triangle ABC$

Vâng, trong bài viết này chúng ta sẽ cùng nhau tìm hiểu về cách tính diện tích của một tam giác bất kì và một số cách tính đặc biệt tương ứng với các tam giác đặc biệt, ví dụ như tam giác vuông, tam giác đều. Nhưng trước tiên bạn cần hiểu diện tích tam giác là gì trước đã.

I. Diện tích tam giác là gì?

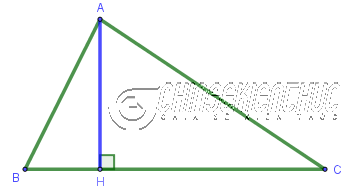
Diện tích tam giác là miền bên trong của tam giác. Bạn cần ghi nhớ định nghĩa trên để phân biệt với chu vi của tam giác (tổng độ dài ba cạnh).

NOTE: Như hình bên dưới thì miền màu xanh lam chính là diện tích của tam giác ABC, còn tổng độ dài ba cạnh (màu xanh lục) chính là chu vi của tam giác ABC.

II.  Cách tính diện tích tam giác (tất cả các trường hợp)

Tuy nhiên, khi cần tính diện tích của các tam giác đặc biệt chúng ta nên sử dụng các công thức đặc biệt của chúng. Bởi nó là phương pháp tối ưu nhất giúp chúng ta tiết kiệm được nhiều thời gian và công sức khi giải bài tập.

Và tất nhiên, trong trường hợp bạn quên mất công thức tính diện tích của một tam giác đặc biệt nào thì thì bạn hoàn toàn có thể sử dụng công thức tính diện tích tam giác thường, sẽ hơi mất thời gian để giải vậy thôi.

Chú ý: Điều ngược lại không đúng, công thức tính diện tích tam giác đặc biệt không thể áp dụng được cho tam giác thường.

#1. Cách tính diện tích tam giác thường

Dưới đây là một số công thức tính diện tích tam giác thường gặp, tùy thuộc vào giả thuyết của bài toán mà chúng ta sẽ chọn lựa cho phù hợp nhất.

1.1. Trường hợp 1: Biết độ dài cạnh đáy và chiều cao tương ứng

Diện tích tam giác sẽ bằng tích một phần hai của độ dài cạnh đáy với chiều cao tương ứng. Hay nói cách khác thì diện tích của một tam giác sẽ bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối diện của đỉnh đó.

Công thức: $S_{ABC}=\frac{1}{2}.BC.AH$

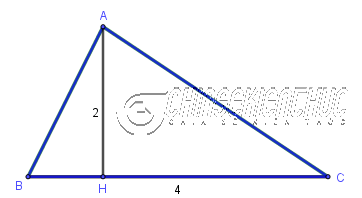
Ví dụ: Cho tam giác ABC có chiều cao AH=2 và độ dài cạnh đáy BC=4. Tính diện tích tam giác đã cho.

Lời giải:

Dễ thấy AH là chiều cao tương ứng với cạnh đáy BC

Áp dụng công thức $S_{ABC}=\frac{1}{2}.BC.AH$ ta được $S_{ABC}= \frac{1}{2}.4.2=4$

=> Vậy diện tích tam giác đã cho là 4 ĐVDT

1.2. Trường hợp 2: Biết độ dài hai cạnh và độ lớn của góc xen giữa

Diện tích tam giác trong trường hợp này sẽ bằng tích của ½ với độ dài 2 cạnh và SIN độ lớn của góc xen giữa..

Công thức: $S_{ABC}=\frac{1}{2}.AC.BC.\sin{\widehat{ACB}}$

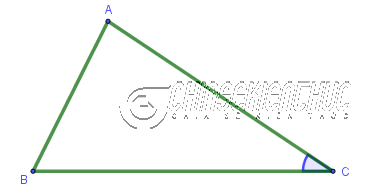
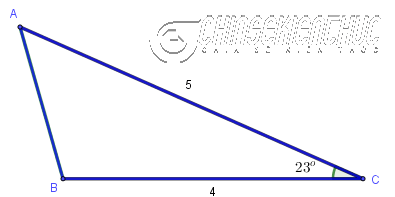
Ví dụ: Cho tam giác ABC có AC=5, BC=4 và $\widehat{ACB}=23^o$. Tính diện tích tam giác đã cho.

Lời giải:

Dễ thấy góc $\widehat{ACB}$ là góc xen giữa cạnh AC và BC

Áp dụng công thức $S_{ABC}=\frac{1}{2}.AC.BC.\sin{\widehat{ACB}}$ ta được $S_{ABC}= \frac{1}{2}.5.4.\sin{23^o} \approx 3.9$

=> Vậy diện tích tam giác đã cho gần bằng 3.9 ĐVDT

1.3. Trường hợp 3: Biết độ dài ba cạnh

Công thức: $S_{ABC}=\sqrt{p(p-a)(p-b)(p-c)}$

Công thức này được đặt tên theo tên của nhà Toán học đã tìm ra nó, đố bạn nhà Toán học đó là ai?

• p là nữa chu vi, $p=\frac{a+b+c}{2}$
• $a=BC, b=AC, c=AB$

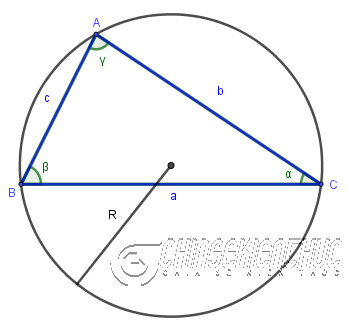
1.4. Trường hợp 4: Biết bán kính đường tròn ngoại tiếp và độ dài ba cạnh hoặc độ lớn ba góc

Công thức: $S_{ABC}=\frac{a.b.c}{4.R}$ hoặc $2.R^2 .\sin{\alpha} .\sin{\beta} .\sin{\gamma}$

• $a=BC, b=AC, c=AB$
• R là bán kính đường tròn ngoại tiếp tam giác ABC
• $\alpha=\widehat{ACB}, \beta=\widehat{ABC}, \gamma=\widehat{BAC}$

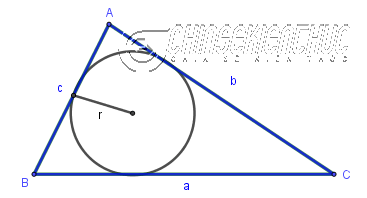
1.5. Trường hợp 5: Biết bán kính đường tròn nội tiếp và độ dài ba cạnh

Diện tích tam giác trong trường hợp này sẽ bằng tích của bán kính đường tròn nội tiếp với nửa chu vi.

Công thức: $S_{ABC}=r.p$

• r bán kính đường tròn nội tiếp
• p là nữa chu vi, $p=\frac{a+b+c}{2}$

#2. Công thức tính diện tích tam giác đặc biệt

Tam giác thường khi có độ dài cạnh hoặc độ lớn góc đặc biệt thì sẽ trở thành tam giác đặc biệt. Cụ thể hơn thì:

• Tam giác thường khi có một góc bằng 90^o thì sẽ trở thành tam giác đặc biệt, ở đây chính là tam giác vuông.
• Tam giác thường khi có ba cạnh bằng nhau thì sẽ trở thành tam giác đặc biệt, ở đây chính là tam giác đều.

2.1. Cách tính diện tích tam giác vuông

Diện tích tam giác vuông sẽ bằng nữa tích hai cạnh góc vuông.

Công thức: $S_{ABC}=\frac{AB.CB}{2}$

2.2. Cách tính diện tích tam giác đều

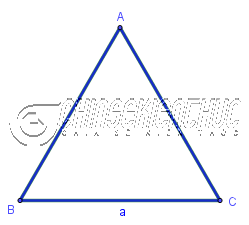
Diện tích tam giác đều cạnh a sẽ bằng tích của một phần tư với a bình phương và căn bậc hai của 3

Công thức: $S_{ABC}=\frac{a^2 \sqrt{3}}{4}$

III. Lời kết

Các công thức tính diện tích tam giác là một trong những công thức tính diện tích quan trọng nhất trong hình học Ơ-clít.

Nhờ vào các công thức này và phương pháp phân hoạch mà chúng ta có thể gián tiếp tính được diện tích của hình bình hành, hình chữ nhật, hình vuông.. Vậy nên, bạn hãy nắm thật chắc các công thức trong bài viết này nhé.

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tính chu vi, diện tích của hình tròn và hình quạt tròn
• Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ hiểu)
• 2 cách tính độ dài cạnh huyền trong tam giác vuông (rất dễ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com