Đường tròn ngoại tiếp tam giác, đường tròn ngoại tiếp tứ giác, đường tròn nội tiếp tam giác, đường tròn bàng tiếp tam giác, … là một trong những đường tròn rất thường gặp trong chương trình Toán học Trung học.
Mỗi đường tròn trên đều có một cách vẽ khác nhau, tuy không quá phức tạp nhưng vì có quá nhiều loại nên nhiều bạn sẽ nhầm lẫn và không vẽ được.
Vậy nên hôm nay mình sẽ hướng dẫn lại cách vẽ đường tròn ngoại tiếp tam giác một cách chi tiết nhất có thể, để nó khắc sâu vào trí nhớ của bạn 🙂
Mục Lục Nội Dung
I. Đường tròn ngoại tiếp tam giác là gì?
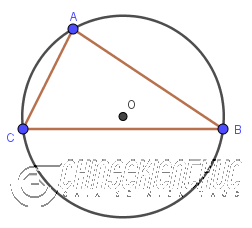
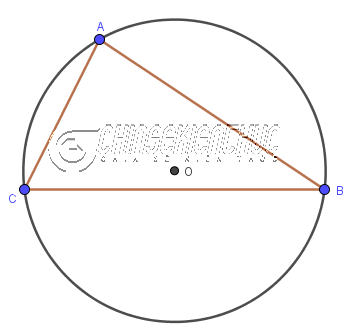
Một đường tròn được gọi là ngoại tiếp tam giác là khi đường tròn đó đi qua ba đỉnh của tam giác, đơn giản vậy thôi.
Bất kì một tam giác nào cũng có một và chỉ một đường tròn ngoại tiếp duy nhất.
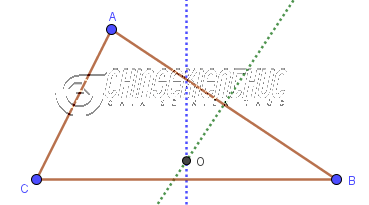
Hình trên là đường tròn tâm O ngoại tiếp tam giác ABC, hay nói cách khác là tam giác ABC nội tiếp đường tròn tâm O.
II. Đường trung trực của một đoạn thẳng
Thông thường muốn vẽ được đường tròn ngoại tiếp tam giác thì chúng ta cần phải biết được vị trí của tâm và bán kính.
- Tâm chính là giao điểm của ba đường trung trực.
- Bán kính chính là khoảng cách từ tâm đến một đỉnh của tam giác.
=> Như vậy công việc đầu tiên mà chúng ta cần phải làm là vẽ đường trung trực của một đoạn thẳng/ một cạnh
Vậy một câu hỏi đặt ra là đường trung trực là đường như thế nào?
Vâng, đường trung trực của một đoạn thẳng là một đường thẳng đi qua tâm của đoạn thẳng đó và vuông góc với đoạn thẳng đó
#1. Các bước vẽ đường trung trực của một đoạn thẳng
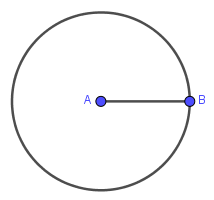
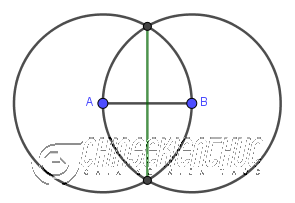
Giả sử chúng ta cần vẽ đường trung trực của đoạn thẳng AB
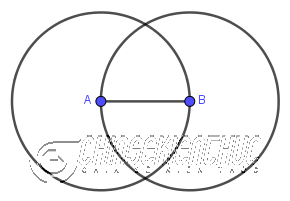
Bước 1. Dựng đường tròn tâm A bán kính AB
Bước 2. Dựng đường tròn tâm B bán kính BA
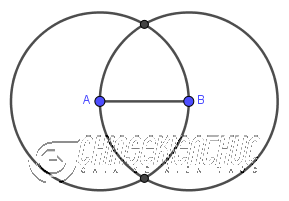
Bước 3. Dựng giao điểm của hai đường tròn
Bước 4. Dựng đường thẳng đi qua hai giao điểm của đường tròn => Đường thẳng vừa dựng chính là đường trung trực của đoạn thẳng AB
#2. Nhận xét về cách vẽ
- Không nhất thiết phải dựng hai đường tròn có bán kính bằng độ dài đoạn thẳng, mà thay vào đó, bạn chỉ cần dựng hai đường tròn có bán kính lớn hơn ½ độ dài đoạn thẳng là được.
- Bạn cũng có thể dựng cung tròn (phù hợp) thay vì phải dựng cả đường tròn.
Chú ý:
Một điều kiện bắt buộc là hai đường tròn hoặc hai cung tròn phải có cùng bán kính.
III. Cách vẽ đường tròn ngoại tiếp tam giác
Ở trên chúng ta vừa tìm hiểu xong cách dựng đường trung trực của một đoạn thẳng rồi, bây giờ chúng ta chỉ cần:
- Dựng hai đường trung trực của hai cạnh bất kì và lấy giao điểm của chúng thì chúng ta sẽ tìm được tâm của đường tròn.
- Bán kính chính là khoảng cách từ tâm đến một đỉnh bất kì của tam giác (đỉnh A, đỉnh B hoặc đỉnh C).
#1. Các bước vẽ đường tròn ngoại tiếp
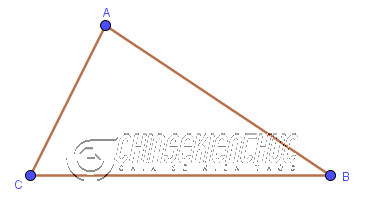
Giả sử chúng ta cần vẽ đường tròn ngoại tiếp tam giác ABC
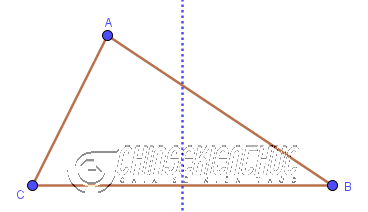
Bước 1. Dựng đường trung trực của đoạn thẳng CB
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
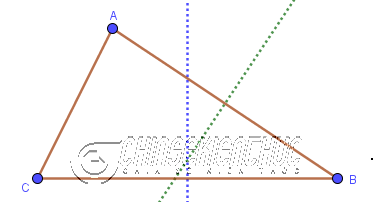
Bước 2. Dựng đường trung trực của đoạn thẳng AB
Bước 3. Dựng giao điểm O của hai đường trung trực
Bước 4. Dựng đường tròn tâm O bán kính OC (hoặc OA, OB)
#2. Nhận xét về cách vẽ trên
- Bạn có thể dựng đường trung trực của hai cạnh khác chứ không nhất thiết phải là CB, AB.
- Bán kính OC hay OB hay OA đều được vì chúng đều bằng nhau.
IV. Lời kết
Như vậy là qua bài viết này thì các bạn đã biết đường tròn ngoại tiếp là gì, cũng như cách vẽ đường tròn ngoại tiếp tam giác rồi đúng không. Nói chung là để vẽ đường tròn ngoại tiếp của một tam giác cũng không có gì khó khăn cả phải không nào !
Trong Toán học thì cách vẽ mà chúng ta vừa thực hiện được gọi là dựng hình. Thông thường người ta chỉ dựng hình bằng thước thẳng và compa.
Sau khi dựng xong cần phải chứng minh cách dựng vừa thực hiện là đúng. Tuy nhiên, trong phạm vi ngắn gọn của bài viết này mình không thực hiện việc chứng minh
Hầu hết chúng ta chỉ cần dựng đúng là được, việc chứng minh chỉ cần thực hiện trong một bài toán dựng hình hoàn chỉnh.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Làm thế nào để vẽ đường tròn nội tiếp tam giác?
- 3 cách vẽ trung điểm của đoạn thẳng mà mình hay áp dụng
- 11 loại góc thường gặp trong hình học nhất định phải biết
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống