11 loại góc thường gặp trong hình học nhất định phải biết

Trong bài viết này mình sẽ trình bày với các bạn toàn bộ các loại góc thường gặp trong chương trình Hình học trung học, chủ yếu nhất là Hình học Trung học cơ sở.

Với mỗi loại góc mình sẽ nêu ra định nghĩa cùng với hình vẽ minh họa tương ứng.

Vì mục đích của bài viết là giúp các bạn biết được tên của góc đã cho và vẽ được góc theo tên đã cho nên mình không trình bày tính chất hoặc định lý hoặc hệ quả có liên quan nhé, các nội dung này sẽ được giới thiệu trong những bài viết tiếp theo.

I. Góc là gì?

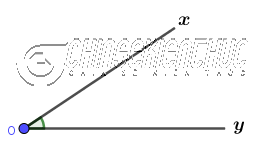
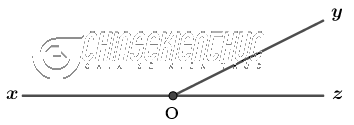
Định nghĩa thì rất đơn giản thôi: Góc là hình được tạo ra bởi hai tia chung gốc.

$\widehat{xOy}$ là hình được tạo bởi hai tia Ox và Oy

II. Góc phụ thuộc vào số đo

• Góc nhọn là góc có số đo nhỏ hơn 90 độ
• Góc vuông là góc có số đo bằng 90 độ
• Góc tù là góc có số đo lớn hơn 90 độ nhưng nhỏ hơn 180 độ
• Góc bẹt là góc có số đo bằng 180 độ hoặc góc tạo bởi hai tia đối nhau

Ngoài ra thì còn có các loại góc khác như:

• Góc phản là góc lớn hơn 180° nhưng nhỏ hơn 360°
• Góc đối đỉnh
• Góc đầy là góc bằng 360° (toàn bộ vòng tròn).

III. Cặp góc phụ thuộc vào tổng số đo

#1. Hai góc phụ nhau

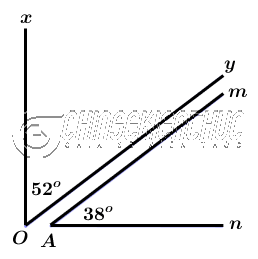
Hai góc được gọi là phụ nhau khi tổng số đo của chúng bằng 90^o

Vì $\widehat{xOy}+\widehat{mAn}=52+38=90$ nên chúng phụ nhau.

#2. Hai góc bù nhau

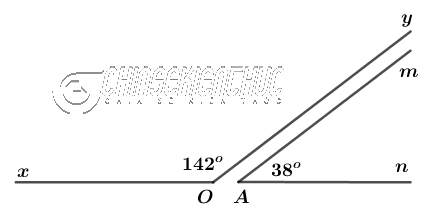
Hai góc được gọi là bù nhau khi tổng số đo của chúng bằng 180^o

Vì $\widehat{xOy}+\widehat{mAn}=142+38=180$ nên chúng bù nhau.

IV. Cặp góc phụ thuộc vào vị trí

#1. Hai góc kề nhau

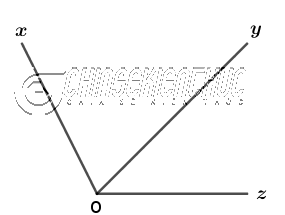
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trong hai mặt phẳng đối nhau, có bờ là cạnh chung.

Vì …

• Oy là cạnh chung của $\widehat{xOy}$ và $\widehat{zOy}$
• Ox và Oz nằm trong hai mặt phải đối nhau có bờ là cạnh chung Oy

… nên $\widehat{xOy}$ và $\widehat{zOy}$ kề nhau

#2. Hai góc kề bù

Hai góc kề bù là hai góc kề nhau và bù nhau. Hai góc kề bù có một cạnh chung và hai cạnh còn lại tạo thành một đường thẳng.

Vì …

• $\widehat{xOy}$ và $\widehat{zOy}$ kề nhau (… phần giải thích giành cho bạn đọc …)
• $\widehat{xOy}$ và $\widehat{zOy}$ bù nhau (… phần giải thích giành cho bạn đọc …)

… nên $\widehat{xOy}$ và $\widehat{zOy}$ kề bù nhau

#3. Hai góc đối đỉnh

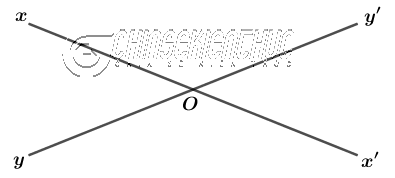
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia.

Vì …

• Ox là tia đối của Ox’
• Oy là tia đối của Oy’
• Ox và Oy lần lượt là hai cạnh của $\widehat{xOy}$
• Ox’ và Oy’ lần lượt là hai cạnh của $\widehat{x’Oy’}$

… nên $\widehat{xOy}$ đối đỉnh với $\widehat{x’Oy’}$

#4. Các góc so le trong, các góc đồng vị

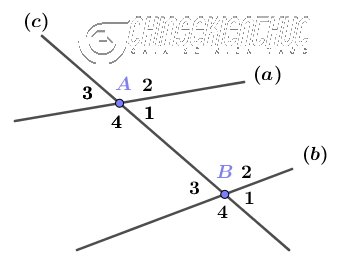
Cho đường thẳng (a) và đường thẳng (b), đường thẳng (c) cắt hai đường thẳng đã cho tại điểm A và điểm B.

Mỗi lần cắt tạo thành bốn góc được đánh số thứ tự như …

… lúc bấy giờ ta có:

• $\widehat{A_1}$ so le trong với $\widehat{B_3}$, $\widehat{A_4}$ so le trong với $\widehat{B_2}$
• Các cặp $\widehat{A_1}$ và $\widehat{B_1}$, $\widehat{A_2}$ và $\widehat{B_2}$, $\widehat{A_3}$ và $\widehat{B_3}$, $\widehat{A_4}$ và $\widehat{B_4}$ đồng vị với nhau.

V. Góc với đường tròn

#1. Góc ở tâm

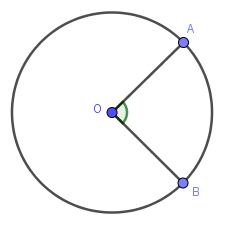
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.

Vì tâm O của đường tròn trung với đỉnh O của $\widehat{AOB}$ nên góc đã cho là một góc ở tâm.

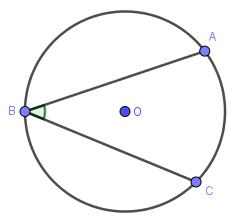
#2. Góc nội tiếp

Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó được gọi là góc nội tiếp.

Vì …

• $\widehat{ABC}$ có đỉnh B nằm trên đường tròn tâm (O)
• Hai cạnh BA, BC lần lượt chứa hai dây cung BA, BC của đường tròn tâm (O)

… nên góc đã cho là một góc nội tiếp.

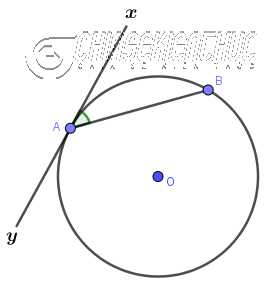
#3. Góc tạo bởi tia tiếp tuyến và dây cung

Cho $xy$ là tiếp tuyến của đường tròn tâm $(O)$, điểm $A$ là tiếp điểm, tia $Ax$ và tia $Ay$ là hai tia đối nhau cũng là hai tia tiếp tuyến.

• $\widehat{BAx}$ có đỉnh là điểm A nằm trên đường tròn
• $\widehat{BAx}$ có cạnh Ax là một tia tiếp tiếp
• $\widehat{BAx}$ có cạnh BA chứa dây cung BA

Vậy $\widehat{BAx}$ hoặc $\widehat{BAy}$ là góc tạo bởi tia tiếp tuyến và dây cung.

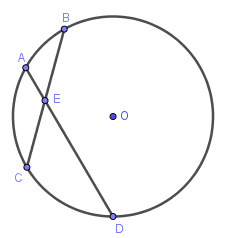
#4. Góc có đỉnh bên trong đường tròn

Vì $\widehat{AEB}$ có đỉnh E nằm bên trong đường tròn nên $\widehat{AEB}$ hoặc $\widehat{CED}$ được gọi là góc có đỉnh bên trong đường tròn.

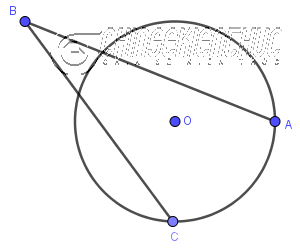
#5. Góc có đỉnh bên ngoài đường tròn

Vì $\widehat{ABC}$ …

• Có đỉnh B nằm bên ngoài đường tròn.
• Cạnh BA, cạnh BC đều có điểm chung với đường trò.

… nên $\widehat{ABC}$ là góc có đỉnh nằm bên ngoài đường tròn

VI. Lời kết

Okay, trên đây là toàn bộ những góc thường gặp nhất trong hình học.

Trong các bài tập thực hành, chúng ta sẽ ít gặp các góc nằm một mình trong một hình đơn giản như trên, mà thường là nó sẽ xuất hiện cùng với nhiều đối tượng hình học khác nhau, chứ không dễ ăn như các ví dụ bên trên đâu 😀

Vì vậy chúng ta cần nắm chắc định nghĩa bằng cách đọc đi đọc lại nhiều lần, kết hợp với việc quan sát hình vẽ minh họa.

Nếu làm được vậy thì khi gặp một hình phức tạp bạn vẫn có thể nhận ra các góc trên một cách dễ dàng, từ đó vận dụng tính chất, định lí, hệ quả, … để giải quyết bài toán một cách dễ dàng hơn.

Hi vọng bài viết này sẽ giúp ích cho bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com