Công thức tính độ dài đường phân giác

Công thức tính độ lớn của góc, độ dài của cạnh, diện tích tam giác thì chắc bạn nào cũng biết rồi, bởi nó quá cơ bản. Không những thế, nhiều bạn còn biết nhiều công thức, nhiều cách tính nữa là đằng khác.

Tuy nhiên, công thức tính độ dài các đường phân giác trong tam giác thì không phải bạn nào cũng biết, thậm chí có bạn còn không biết đến sự tồn tại của công thức này.

Mấy hôm trước, trong một lần tình cờ đọc quyển Hình học sơ cấp và thực hành giải toán mà mình đã nhìn thấy công thức này và khá ấn tượng với nó.

Vậy nên hôm nay mình sẽ chia sẻ với các bạn công tính độ dài các đường phân giác trong tam giác, đồng thời chứng minh tính đúng đắn của nó.

#1. Nhắc lại một số công thức có liên quan

Để chứng minh được công thức tính độ dài các đường phân giác trong tam giác thì ít nhất bạn phải thuộc được công thức tính diện tích tam giác và các công thức lượng giác có liên quan.

1.1. Công thức tính diện tích tam giác

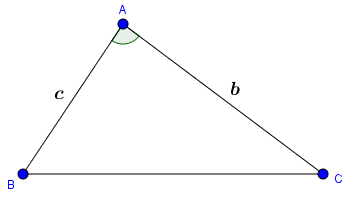
Có nhiều công thức tính diện tích tam giác, tuy nhiên ở đây chúng ta chỉ quan tâm đến công thức: $S_{ABC}=\frac{1}{2}bc\sin A$

1.2. Công thức biến đổi lượng giác

Tương tự công thức tính diện tích tam giác, công thức biến đổi lượng giác cũng có rất nhiều.

Tuy nhiên ở đây chúng ta chỉ quan tâm đến công thức nhân đôi, công thức hạ bậc, hệ quả của định lý côsin và các dạng tương đương.

• Công thức nhân đôi $\sin2A=2\sin A\cos A \Leftrightarrow \sin A=2\sin\frac{A}{2}\cos\frac{A}{2}$
• Công thức hạ bậc $\cos^2A=\frac{1+\cos2A}{2} \Leftrightarrow \cos^2\frac{A}{2}=\frac{1+\cos A}{2} \Leftrightarrow 2\cos^2\frac{A}{2}=1+\cos A$
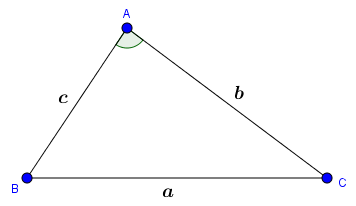
• Hệ quả của định lý côsin $\cos A=\frac{b^2+c^2-a^2}{2bc}$

#2. Công thức tính độ dài các đường phân giác

Tạm thời chúng ta sẽ thừa nhận tính đúng đắn của các công thức bên dưới, tuy nhiên cũng cần phải chứng minh lại.

Việc chứng minh không chỉ khẳng định được tính đúng đắn của công thức mà còn giúp chúng ta nhớ được công thức một cách lâu hơn và chính xác hơn.

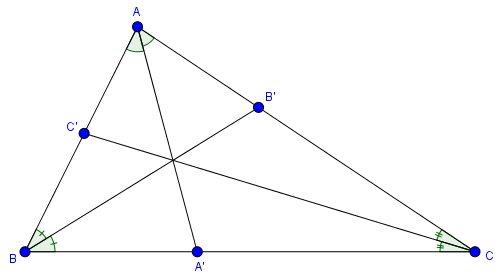
Tam giác $ABC$ có $AA’, BB’, CC’$ lần lượt là các đường phân giác của $\hat{A}, \hat{B}, \hat{C}$

Đặt $AB=c, BC=a, CA=b, AA’=l_{a}, BB’=l_b, CC’=l_c$

Lúc này độ dài các đường phân giác của tam giác $ABC$ sẽ được tính theo các công thức $l_a=\frac{2\sqrt{p(p-a)bc}}{b+c}$, $l_b=\frac{2\sqrt{p(p-b)ca}}{c+a}$, $l_c=\frac{2\sqrt{p(p-c)ab}}{a+b}$

#3. Chứng minh công thức tính độ dài các đường phân giác

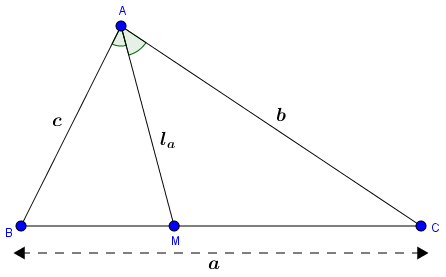
Để tiết kiệm thời gian mình chỉ chứng minh cho công thức $l_a=\frac{2\sqrt{p(p-a)bc}}{b+c}$, hai công thức còn lại các bạn chứng minh hoàn toàn tương tự.

Bắt đầu chứng minh …

Vì $l_a$ là đường phân giác của $\hat{A}$ nên $S_{ABM}+S_{ACM}=S_{ABC}$ $(1)$

$(1) \Leftrightarrow \frac{1}{2}cl_a\sin\frac{A}{2}+\frac{1}{2}bl_a\sin\frac{A}{2}=\frac{1}{2}bc\sin A$

$(1) \Leftrightarrow cl_a\sin\frac{A}{2}+bl_a\sin\frac{A}{2}=bc\sin A$

$(1) \Leftrightarrow (c+b)l_a\sin\frac{A}{2}=bc\sin A$ $(2)$

Chúng ta đã biết công thức nhân đôi $\sin2A=2\sin A\cos A \Leftrightarrow \sin A=2\sin\frac{A}{2}\cos\frac{A}{2}$

Thay $\sin A=2\sin\frac{A}{2}\cos\frac{A}{2}$ vào $(2)$ ta được $(c+b)l_a\sin\frac{A}{2}=2bc\sin\frac{A}{2}\cos\frac{A}{2}$ $(3)$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

$(3) \Leftrightarrow (c+b)l_a=2bc\cos\frac{A}{2}$

$(3) \Leftrightarrow l_a=\frac{2bc}{b+c}\cos\frac{A}{2}$ $(*)$

Đến đây chúng ta đã tìm được công thức tính độ dài đường phân giác của $\hat{A}$

Công thức này đã khá là ngắn gọn và có thể chấp nhận được rồi. Tuy nhiên với công thức này, nếu muốn tính được độ dài đường phân giác của $\hat{A}$ thì vẫn phải biết độ lớn của $\hat{A}$

Để tính được trực tiếp thông qua độ dài ba cạnh của tam giác chúng ta cần tiếp tục biến đổi …

Chúng ta đã biết công thức hạ bậc $\cos^2 A=\frac{1+\cos 2A}{2} \Leftrightarrow \cos^2 \frac{A}{2}=\frac{1+\cos A}{2} \Leftrightarrow 2 \cos^2 \frac{A}{2}=1+\cos A$ và hệ quả của định lí côsin $\cos A=\frac{b^2+c^2-a^2}{2bc}$

Xét $2\cos^2 \frac{A}{2}=1+\cos A$ $(4)$

$(4) \Leftrightarrow 2\cos^2 \frac{A}{2}=1+\frac{b^2+c^2-a^2}{2bc}$

$(4) \Leftrightarrow 2\cos^2 \frac{A}{2}=\frac{2bc+b^2+c^2-a^2}{2bc}$

$(4) \Leftrightarrow 2\cos^2 \frac{A}{2}=\frac{(b+c)^2-a^2}{2bc}$

$(4) \Leftrightarrow 2\cos^2 \frac{A}{2}=\frac{(b+c+a)(b+c-a)}{2bc}$

$(4) \Leftrightarrow 2\cos^2 \frac{A}{2}=\frac{b+c+a}{2}\frac{b+c+a-a-a}{bc}$ $(5)$

Chúng ta đã biết công thức nửa chu vi tam giác $p=\frac{a+b+c}{2}$

Thay $p=\frac{a+b+c}{2}$ vào $(5)$ ta được $2\cos^2 \frac{A}{2}=p\frac{2p-2a}{bc}$ $(6)$

$(6) \Leftrightarrow 2\cos^2 \frac{A}{2}=\frac{2p(p-a)}{bc}$

$(6) \Leftrightarrow \cos^2 \frac{A}{2}=\frac{p(p-a)}{bc}$

$(6) \Rightarrow \cos \frac{A}{2}=\sqrt{\frac{p(p-a)}{bc}}$

Thay $\cos \frac{A}{2}=\sqrt{\frac{p(p-a)}{bc}}$ vào $(*)$ ta được $l_a=\frac{2bc}{b+c}\sqrt{\frac{p(p-a)}{bc}}$

Vậy $l_a=\frac{2bc}{b+c}\sqrt{\frac{p(p-a)}{bc}}=\frac{2bc}{b+c}\frac{\sqrt{p(p-a)}}{\sqrt{bc}}=\frac{2bc}{b+c}\frac{\sqrt{p(p-a)}\sqrt{bc}}{\sqrt{bc}\sqrt{bc}}=\frac{2bc}{b+c}\frac{\sqrt{p(p-a)bc}}{bc}=\frac{2\sqrt{p(p-a)bc}}{b+c}$

Chứng minh hoàn thành …

Mình đã có gắng trình bày chi tiết nhất có thể, chỉ cần cố rắng đọc thì mình tin chắc là các bạn sẽ hiểu được thôi 🙂

#4. Lời kết

Ngoài công thức tính độ dài các đường phân giác mà mình vừa trình bày, còn một số công thức khác nữa, tuy nhiên công thức của mình có một số ưu điểm đó là:

• Khá ngắn gọn và dễ nhớ.
• Không cần biết độ lớn của góc tương ứng.
• Không cần sử dụng đến các phép tính lượng giác.
• Thích hợp với học sinh Trung học cơ sở vì ở cấp học này các em chưa có nhiều kiến thức về lượng giác.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn