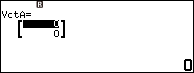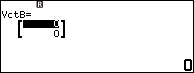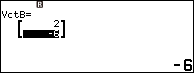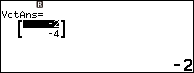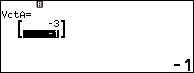Cách bấm máy tính viết phương trình đường phân giác

Việc viết phương trình đường phân giác trong của tam giác khi biết tọa độ ba đỉnh bằng phương pháp Toán học khá là rườm rà và mất thời gian.

Rõ ràng rồi, trước tiên các bạn cần viết phương trình đường thẳng đi qua hai cạnh của góc, tiếp theo là áp dụng công thức:

$\frac{ A_1x+B_1y+C_1}{\sqrt{A_1^2+B_1^2}}=\pm\frac{A_2x+B_2y+C_2}{\sqrt{A_2^2+B_2^2}}$

Rồi sau cùng là xác định đường nào là đường phân giác trong.

Vâng, đó là các bước để viết phương trình đường phân giác trên mặt phẳng, còn trong không gian nó còn rườm rà hơn thế nữa  >.<

Biết được khó khăn trên, hôm nay, mình sẽ hướng dẫn các bạn sử dụng máy tính CASIO viết nhanh phương trình đường phân giác trong của tam giác khi biết tọa độ ba đỉnh.

Nếu thấy hay thì đừng quên chia sẻ bài viết này cho bạn bè cùng tham khảo nữa nhé, đừng giấu bài nha :))

#1. Các bước bấm máy viết phương trình đường phân giác

#2. Bấm máy tính viết phương trình đường phân giác (Casio fx 880 BTG)

Ví dụ 1. Viết phương trình đường phân giác trong của góc A của tam giác ABC biết điểm A=(4, 4), B=(1, 3) và C(6, -2)

Bước 1. Tính véc tơ $\overrightarrow{AB}$ và véc tơ $\overrightarrow{AC}$

Dễ thấy $\overrightarrow{AB}=(-3, -1)$ và $\overrightarrow{AC}=(2, -6)$

Bước 2. Mở tính năng tính toán véc tơ Vector

Nhấn phím HOME => chọn Vector => nhấn phím EXE

Bước 3. Lần lượt gán véc tơ $\overrightarrow{AB}=(-3, -1)$ và véc tơ $\overrightarrow{AC}=(2, -6)$ vào biến nhớ véc tơ VctA và VctB

Bước 3.1. Gán véc tơ $\overrightarrow{AB}=(-3, -1)$ vào biến nhớ véc tơ VctA

Nhấn phím TOOLS => chọn VctA => nhấn phím OK => chọn Confirm => nhấn phím OK

Nhập -3 => nhấn phím EXE => nhập -1 => nhấn phím EXE

Nhấn phím EXE

Bước 3.2. Gán véc tơ $\overrightarrow{AC}=(2, -6)$ vào biến nhớ véc tơ VctB

Nhấn phím TOOLS => chọn VctB => nhấn phím OK => chọn Confirm => nhấn phím OK

Nhập 2 => nhấn phím EXE => nhập -6 => nhấn phím EXE

Nhấn phím EXE

Bước 4. Nhập $(UnitV(VctA) + UnitV(VctB)) \times Abs(VctA)$ => nhấn phím EXE

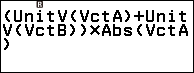
Gợi ý:

• Nhấn để nhập UnitV
• Nhấn để nhập VctA
• Nhấn để nhập VctB
• Nhấn để nhập Abs

Suy ra (-2, -4) là véc tơ chỉ phương của đường phân giác trong của góc A

Vậy phương trình đường phân giác cần tìm là $\frac{x-4}{-2}=\frac{y-4}{-4}$

Ví dụ 2. Viết phương trình đường phân giác trong của góc B của tam giác ABC biết điểm A=(1, 2, -1), B=(2, -1, 3) và C(-4, 7, 5)

Các bạn thực hiện tương tự Bước 1 đến Bước 4 của Ví dụ 1 ngoại trừ Bước 3.1 và Bước 3.2

Dễ thấy $\overrightarrow{BA}=(-1, 3, -4)$ và $\overrightarrow{BC}=(-6, 8, 2)$

Bước 3.1. Nhấn phím TOOLS => chọn VctA => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

Bước 3.2. Nhấn phím TOOLS => chọn VctB => nhấn phím OK => nhấn phím OK => chọn 3 Dimensions => nhấn phím OK => nhấn phím OK

Suy ra (-4, 7, -3) là véc tơ chỉ phương của đường phân giác trong của góc B

Vậy phương trình đường phân giác cần tìm $\frac{x-2}{-4}=\frac{y+1}{7}=\frac{z-3}{-3}$

Xem video thao tác trên máy Casio 880 BTG

#3. Cách viết phương trình đường phân giác trên fx 580 VN X

Ví dụ 3. Viết phương trình đường phân giác trong của góc A của tam giác ABC biết điểm A=(4, 4), B=(1, 3) và C(6, -2)

Bước 1. Tính véc tơ $\overrightarrow{AB}$ và véc tơ $\overrightarrow{AC}$

Dễ thấy $\overrightarrow{AB}=(-3, -1)$ và $\overrightarrow{AC}=(2, -6)$

Bước 2. Mở tính năng tính toán véc tơ Vector

Nhấn phím MENU => chọn Vector => nhấn phím = => nhấn phím AC

Bước 3. Lần lượt gán véc tơ $\overrightarrow{AB}=(-3, -1)$ và véc tơ $\overrightarrow{AC}=(2, -6)$ vào biến nhớ véc tơ VctA và VctB

Bước 3.1. Gán véc tơ $\overrightarrow{AB}=(-3, -1)$ vào biến nhớ véc tơ VctA

Nhấn phím OPTN => nhấn phím 1 => nhấn phím 1 => nhấn phím 2

Nhập -3 => nhấn phím = => nhập -1 => nhấn phím =

Nhấn phím AC

Bước 3.2. Gán véc tơ $\overrightarrow{AC}=(2, -6)$ vào biến nhớ véc tơ VctB

Nhấn phím OPTN => nhấn phím 1 => nhấn phím 2 => nhấn phím 2

Nhập 2 => nhấn phím = => nhập -6 => nhấn phím =

Nhấn phím AC

Bước 4. Nhập $(UnitV(VctA) + UnitV(VctB)) \times Abs(VctA)$ => nhấn phím =

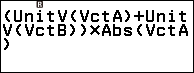
Gợi ý:

• Nhấn phím để nhập UnitV
• Nhấn phím để nhập VctA
• Nhấn phím để nhập VctB

Suy ra (-2, -4) là véc tơ chỉ phương của đường phân giác trong của góc A

Vậy phương trình đường phân giác cần tìm $\frac{x-4}{-2}=\frac{y-4}{-4}$

Ví dụ 4. Viết phương trình đường phân giác trong của góc B của tam giác ABC biết điểm A=(1, 2, -1), B=(2, -1, 3) và C(-4, 7, 5)

Các bạn làm tương tự từ Bước 1 đến Bước 4 của Ví dụ 3 bên trên, ngoại trừ Bước 3.1 và Bước 3.2

Dễ thấy $\overrightarrow{BA}=(-1, 3, -4)$ và $\overrightarrow{BC}=(-6, 8, 2)$

Bước 3.1. Nhấn phím OPTN => nhấn phím 1 => nhấn phím 1 => nhấn phím 3

Bước 3.2. Nhấn phím OPTN => nhấn phím 1 => nhấn phím 2 => nhấn phím 3

Suy ra (-4, 7, -3) là véc tơ chỉ phương của đường phân giác trong của góc B

Vậy phương trình đường phân giác cần tìm $\frac{x-2}{-4}=\frac{y+1}{7}=\frac{z-3}{-3}$

Xem video thao tác trên máy Casio 580 VNX

#4. Lời kết

Thủ thuật sử dụng máy tính CASIO này sẽ giúp các bạn xác định nhanh phương trình đường phân giác trong của tam giác khi biết tọa độ 3 đỉnh, không phân biệt trên mặt phẳng hay trong không gian.

Mặc dù trong một số trường hợp chúng ta không thu được giá trị nguyên (tọa độ của véc tơ chỉ phương).

Nhưng dựa vào những giá trị thu được thì chúng ta vẫn chọn được phương án đúng (trắc nghiệm), hoặc là dùng để kiểm tra kết quả (tự luận)

Hi vọng những thủ thuật trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha.

Đọc thêm:

• Cách viết phương trình đường phân giác
• Cách tính độ dài đường phân giác trong tam giác
• Cách viết phương trình đường cao trong tam giác
• Cách viết phương trình đường tròn nội tiếp tam giác

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn