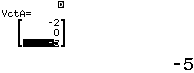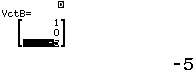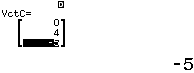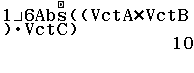Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Hôm nay mình sẽ hướng dẫn cho các bạn cách tính thể tích tứ diện trong không gian, ở đây mình sẽ trình bày cách tính thông qua tích có hướng và tích vô hướng của hai véc-tơ (không dùng tích hỗn hợp/ tích hỗn tạp, ma trận).
Lựa chọn phương pháp này tuy làm cho công thức tính rườm rà hơn nhưng bù lại nó dễ hiểu hơn, đặc biệt là với các bạn học sinh.
Ngoài ra, vì trắc nghiệm đang là xu hướng chủ đạo của bộ giáo dục nên mình cũng sẽ hướng dẫn thêm cho các bạn thủ thuật tính nhanh bằng máy tính CASIO fx-580VN X
Đọc thêm:
Mục Lục Nội Dung
#1. Cách tính tích có hướng của hai véc-tơ
Cho $\vec{u}=(x; y; z), \vec{v}=(x’; y’; z’)$ khi đó tích có hướng của $\vec{u}$ và $\vec{v}$ sẽ được tính theo công thức $(yz’-y’z; zx’-z’x; xy’-x’y)$
Chú ý:
- Tích có hướng của véc-tơ $\vec{v}$ và $\vec{v}$ thường được kí hiệu là $[\vec{u}; \vec{v}]$
- Tích có hướng của hai véc-tơ là một véc-tơ
#2. Cách tính tích vô hướng của hai véc-tơ
Cho $\vec{u}=(x; y; z), \vec{v}=(x’; y’; z’)$ khi đó tích vô hướng của $\vec{u}$ và $\vec{v}$ sẽ được tính theo công thức $xx’+yy’+zz’$
Chú ý:
- Tích vô hướng của véc-tơ $\vec{u}$ và $\vec{v}$ thường được kí hiệu là $\vec{u} \cdot \vec{v}$
- Tích vô hướng của hai véc-tơ là một số thực
#3. Thuật toán tính thể tích của một tứ diện
Tính thể tích tứ diện ABCD biết $A=(x_1; y_1; z_1), B=(x_2; y_2; z_2), C=(x_3; y_3; z_3), D=(x_4; y_4; z_4)$
Bước 1. Tính $\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}$
$\overrightarrow{AB}=(x_2-x_1; y_2-y_1; z_2-z_1), \overrightarrow{AC}=(x_3-x_1; y_3-y_1; z_3-z_1), \overrightarrow{AD}=(x_4-x_1; y_4-y_1; z_4-z_1)$
Bước 2. Tính tích có hướng của $\overrightarrow{AB}$ và $\overrightarrow{AC}$
Bước 3. Tính tích vô hướng của $[\overrightarrow{AB}; \overrightarrow{AC}]$ và $\overrightarrow{AD}$
Bước 4. Tính giá trị biểu thức $\frac{1}{6}|[\overrightarrow{AB}; \overrightarrow{AC}] \cdot \overrightarrow{AD}|$
#4. Ví dụ minh họa
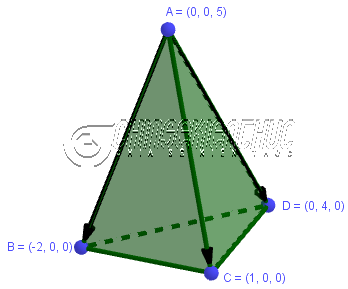
Tính thể tích tứ diện ABCD biết $A=(0; 0; 5), B=(-2; 0; 0), C=(1; 0; 0), D=(0; 4; 0)$
Bước 1. Tính $\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}$
$\overrightarrow{AB}=(-2; 0; -5), \overrightarrow{AC}=(1; 0; -5), \overrightarrow{AD}=(0; 4; -5)$
Bước 2. Tính tích có hướng của $\overrightarrow{AB}$ và $\overrightarrow{AC}$
$[\overrightarrow{AB}; \overrightarrow{AC}]=(0; -15; 0)$
Bước 3. Tính tích vô hướng của $[\overrightarrow{AB}, \overrightarrow{AC}]$ và $\overrightarrow{AD}$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
$[\overrightarrow{AB}, \overrightarrow{AC}] \cdot \overrightarrow{AD}=-60$
Bước 4. Tính giá trị biểu thức $\frac{1}{6}|[\overrightarrow{AB}, \overrightarrow{AC}] \cdot \overrightarrow{AD}|$
$\frac{1}{6}|-60|=10$
=> Vậy thể tứ diện ABCD bằng 10 ĐVTT
#5. Thủ thuật tính nhanh bằng máy tính CASIO fx-580VN X
Bước 1. Chọn phương thức tính toán Vector
Bước 2. Gán véc-tơ $\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}$ lần lượt vào các véc-tơ VctA, VctB, VctC
Bước 3. Tính giá trị biểu thức $\frac{1}{6}Abs((VctA \times VctB) \cdot VctC)$
Chú ý:
- $Abs$ là hàm tính giá trị tuyệt đối của một số thực
- $\times$ là tính tích có hướng của hai véc-tơ
- $\cdot$ là tính tích vô hướng của hai véc-tơ
#6. Lời kết
Vậy là mình đã hướng dẫn xong cho các bạn cách tính thể tích tứ diện trong không gian bằng phương pháp thuật giải và bằng phương pháp máy tính CASIO fx-580VN X rồi nhé.
Tùy thuộc yêu cầu cụ thể mà các bạn cân nhắc chọn lựa cách giải cho phù hợp, dễ thấy phương pháp thuật giải phù hợp với bài thi tự luận, còn phương pháp máy tính CASIO phù hợp với bài thi trắc nghiệm hơn.
Ngoài ra, khi được yêu cầu tính thể tích của hình hộp thì cách tính cũng hoàn toàn tương tự, nhưng bạn nhớ nhân thêm 6 ở kết quả cuối cùng.
Hay nói cách khác là thể tích của hình hộp gấp 6 lần thể tích của hình tứ diện (cùng một hệ bốn điểm). Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
