Cách tính diện tích và thể tích của hình trụ (có ví dụ)

Mến chào tất cả các bạn, hôm nay chúng ta sẽ cùng nhau tìm hiểu cách tính diện tích xung quanh của hình trụ, tính diện tích toàn phần của hình trụ và cách để tính thể tích của hình trụ. Nói chung là những công thức liên quan đến hình trụ.

Tương tự như hình nón và hình cầu, hình trụ cũng là một loại khối tròn xoay thường gặp trong Toán học, cũng như có ứng dụng rất nhiều trong thực tiễn của cuộc sống.

I. Hình trụ là gì?

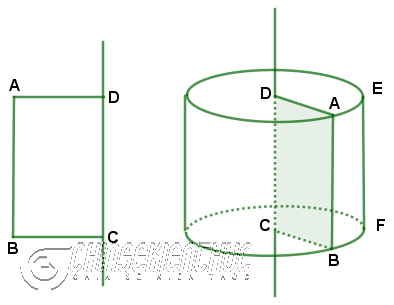
Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định thì chúng ta sẽ thu được một hình trụ.

Bạn có thể hiểu: Hình trụ là hình gồm có 2 đáy là 2 hình tròn nằm song song và có kích thước bằng nhau.

Hoặc: Hình trụ là hình được giới hạn bởi mặt trụ và hai đường tròn có đường kính bằng nhau.

Sở dĩ mình đưa ra nhiều khái niệm cho các bạn là để các bạn có thể dễ nhớ và dễ hình dung hơn, bạn có thể nhớ theo ý hiểu nào cũng được nhé.

Sau khi quay cạnh …

• DA, CB sẽ tạo ra hai đáy của hình trụ, hai đáy này là hai hình tròn bằng nhau và song song với nhau
• AB sẽ tạo ra mặt xung quanh của hình trụ, mỗi một vị trí của AB được gọi là một đường sinh

Vì đường sinh EF và các đường sinh khác vuông góc với hai hình tròn đáy nên độ dài của đường sinh chính là chiều cao của hình trụ.

Hộp sữa, hộp cá mồi, ống nghiệm, ly thủy tinh, … là những hình ảnh thực tế thường gặp của hình trụ.

II. Công thức tính diện tích hình trụ

Trước khi đến với công thức tính diện tích xung quanh của hình trụ và công thức tính diện tích toàn phần của hình trụ thì chúng ta sẽ cùng nhau tìm hiểu cách mà người ta xây dựng công thức này trước đã.

Bước 1. Cắt rời hai đáy của hình trụ

Bước 2. Cắt dọc theo đường sinh

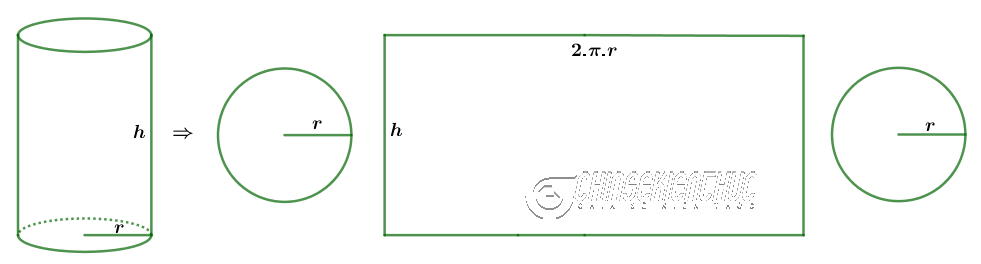
Bước 3. Trải phẳng các hình cắt được ở Bước 1 và Bước 2

Dễ thấy hình cắt được ở Bước 1 là hai hình tròn có cùng diện tích và ở Bước 2 là một hình chữ nhật (có độ dài một cạnh là chu vi của đường tròn đáy và cạnh còn lại là chiều cao)

Mặc khác, chúng ta đã biết công thức tính diện tích hình tròn và công thức tính diện tích hình chữ nhật rồi.

=> Công thức tính diện tích xung quanh và diện tích toàn phân của hình trụ lần lượt là …

#1. Công thức tính diện tích xung quanh của hình trụ

…. sẽ bằng tích của 2, $\pi$, độ dài bán bán kính và chiều cao.

Công thức: $S_{xq}=2.\pi.r.h$

#2. Công thức tính diện tích toàn phần của hình trụ

…. sẽ bằng tổng của diện tích xung quanh và hai lần diện tích hình tròn đáy.

Công thức: $S_{tp}=s_{xq}+2.\pi.r^2=2.\pi.r.h+2.\pi.r^2$

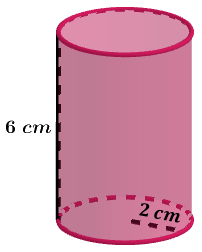
Ví dụ 1: Tính diện tích xung quanh và diện tích toàn phần của hình trụ biết bán kính của hình tròn đáy bằng 2 cm và chiều cao bằng 6 cm

Lời Giải:

Áp dụng công thức $2.\pi.r.h$ vào hình trụ đã cho ta được $2.\pi.2.6=24.\pi \approx 75.4~cm^2$

Áp dụng công thức $2.\pi.r.h+2.\pi.r^2$ vào hình trụ đã cho ta được $24.\pi+2.\pi.2^2=32.\pi \approx 100.5~cm^2$

=> Vậy diện tích xung quanh và diện tích toàn phần của hình trụ đã cho lần lượt gần bằng $75.4~cm^2$ và $100.5~cm^2$

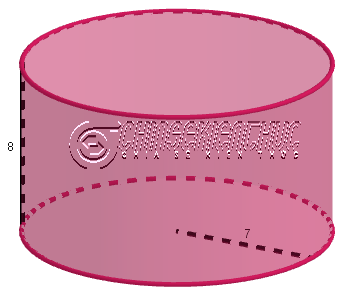
Ví dụ 2: Tìm chiều cao của hình trụ biết bán kính đáy và diện tích xung quanh lần lượt bằng $7~cm$ và $352~cm^2$

Lời Giải:

Diện tích xung quanh của hình trụ được tính theo công thức $2.\pi.r.h$

Mặc khác ta đã có bán kính đường tròn đáy là $7~cm$ và diện tích xung quanh là $352~cm^2$

Suy ra $2.\pi.7.h=352 \Leftrightarrow h=\frac{352}{14.\pi} \approx 8~cm$

=> Vậy chiều cao của hình trụ đã cho gần bằng $8~cm$

III. Công thức tính thể tích hình trụ

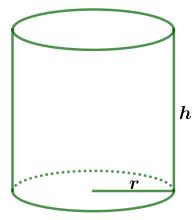
Thể tích của hình trụ sẽ bằng tích của $\pi$, bình phương độ dài bán kính và chiều cao.

Công thức: $V=\pi.r^2.h$

 

Ví dụ 3: Tính thể tích của hình trụ biết bán kính của đường tròn đáy bằng 2 cm và chiều cao bằng 6 cm

Lời Giải:

Áp dụng công thức $\pi.r^2.h$ vào hình trụ đã cho ta được $\pi.2^2.h=24.\pi \approx 75.4~cm^3$

Vậy thể tích của hình trụ đã cho gần bằng $75.4~cm^3$

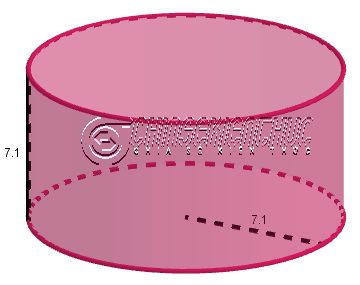
Ví dụ 4: Tính bán kính đường tròn đáy và thể tích của hình trụ biết bán kính đường tròn đáy bằng với chiều cao và diện tích xung quanh bằng $314~cm^2$

Lời Giải:

Diện tích xung quanh của hình trụ được tính theo công thức $2.\pi.r.h$

Mặc khác vì bán kính đường tròn đáy bằng chiều cao nên diện tích xung quanh của hình trụ đã cho sẽ được tính theo công thức $2.\pi.r.r$

Suy ra $2.\pi.r.r=314 \Rightarrow r=\sqrt{\frac{314}{2.\pi}} \approx 7.1~cm$

Áp dụng công thức $\pi.r^2.h$ vào hình trụ đã cho ta được $\pi.\sqrt{\frac{314}{2.\pi}}^2. \sqrt{\frac{314}{2.\pi}}=\frac{157.\sqrt{314}}{\sqrt{2.\pi}} \approx 1109.9~cm^3$

Vậy bán kính của đường tròn đáy và thể tích của hình trụ đã cho lần lượt gần bằng $7.1~cm$ và $1109.9~cm^3$

IV. Lời kết

Khi tính diện tích xung quanh của hình trụ, diện tích toàn phần của hình trụ và thể tích của hình trụ, hay các khối tròn xoay khác mà có sử dụng hằng số $\pi$ thì các bạn nên làm tròn số ở phép tính cuối cùng thôi nhé.

Bởi nếu thực hiện nhiều phép tính và công thức trung gian mà bạn làm tròn số liên tục thì kết quả sau cùng sẽ bị sai số không hề nhỏ

Trường hợp bạn là giáo viên thì nên quy ước hằng số $\pi$ bằng bao nhiêu để thuận lợi cho học sinh cũng như bản thân chúng ta trong lúc chấm bài.

Hi vọng những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com