Cách tính diện tích mặt cầu và thể tích hình cầu (có ví dụ)

Xin chào tất cả các bạn, trong bài viết này mình sẽ hướng dẫn cho các bạn cách tính diện tích của mặt cầu, cũng như tính thể tích của hình cầu một cách chi tiết và đầy đủ nhất có thể.

Chi tiết và đầy đủ như thế nào?

Vâng, đầu tiên mình sẽ trình bày định nghĩa, tiếp theo là công thức tính và cuối cùng là cho ví dụ minh họa. Okay, let’s go //

#1. Hình cầu là gì?

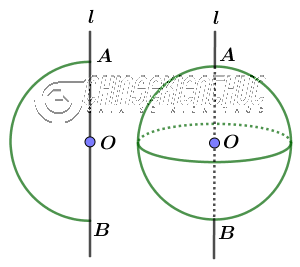
Khi quay nửa hình tròn tâm O bán kính R một vòng quanh đường kính AB cố định thì chúng ta sẽ được một hình cầu.

Hay nói cách khác: Hình cầu là hình được tạo ra khi chúng ta thực hiện quay một nửa hình tròn một vòng quanh đường kính của hình tròn đó.

#2. Mặt cầu là gì?

Và như các bạn có thể thấy ở hình bên dưới, nửa đường tròn trong phép quay vừa thực hiện đã tạo ra mặt cầu (Sphere).

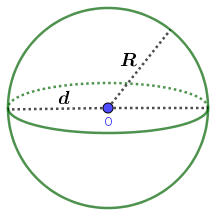
Hay nói cách khác: Mặt cầu là tập hợp các điểm cách đều tâm O cố định cho trước một khoảng không đổi,  bằng với bán kính R.

#3. Công thức tính diện tích mặt cầu

Diện tích của mặt cầu sẽ bằng tích của bốn, $\pi$, bình phương độ dài bán kính hoặc tích của $\pi$, bình phương độ dài đường kính

Công thức: $S_{(O; R)}=4.\pi.R^2=\pi.d^2$

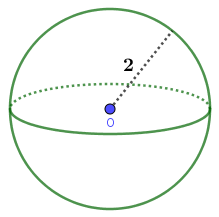
Ví dụ 1: Tính diện tích mặt cầu tâm O bán kính 2 cm

Diện tích mặt cầu tâm O bán kính 2 sẽ bằng $4.\pi.R^2=4.\pi.2^2=16.\pi \approx 50.3~cm^2$

Ví dụ 2: Tính đường kính d’ của mặt cầu tâm O’ bán kính R’. Biết …

• Diện tích của mặt cầu tâm O’ bán kính R’ gấp ba lần diện tích của mặt cầu tâm O bán kính R
• Diện tích của mặt cầu tâm O bán kính R bằng $36~cm^2$

Lời Giải:

Vì diện tích của mặt cầu (O’, R’) gấp ba lần mặt cầu (O, R) nên ta có $\pi.d’^2=3 \times 36 \Leftrightarrow \pi.d’^2=108 \Leftrightarrow d’^2=\frac{108}{\pi}$

Suy ra $d’=\sqrt{\frac{108}{\pi}} \approx 5.9~cm$

Vậy đường kính d’ của mặt cầu tâm O’ bán kính R’ gần bằng $5.9~cm$

#4. Công thức tính thể tích hình cầu

Thể tích của hình cầu sẽ bằng tích của 4/3, $\pi$ và lập phương độ dài bán kính hoặc bằng tích của 1/6, $\pi$ và lập phương độ dài đường kính.

Công thức: $V_{(O; R)}=\frac{4}{3}.\pi.R^3=\frac{1}{6}.\pi.d^3$

Ví dụ 3: Tính thể tích của hình cầu tâm O bán kính 3 cm

Thể tích hình cầu tâm O bán kính 3 sẽ bằng $\frac{4}{3}.\pi.R^3=\frac{4}{3}.\pi.3^3=36.\pi \approx 113.1~cm^3$

Ví dụ 4: Một cái chậu nuôi cá có dạng hình cầu lâu ngày cần phải thay nước. Biết …

• Chậu có đường kính bằng 22 cm
• Lượng nước trong chậu chiếm $\frac{2}{3}$ thể tích của chậu

Tính số lít nước cần chuẩn bị

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Lời Giải:

Lượng nước cần thay được tính bằng lít nên chúng ta cần đổi độ dài đường kính từ 22 cm sang 2.2 dm

Vì chậu nuôi cá có dạng hình cầu nên thể tích của chậu sẽ được tính theo công thức $\frac{1}{6}.\pi.d^3$

Suy ra $\frac{2}{3} \times \frac{1}{6} \times \pi \times (2.2)^3=\frac{1331}{1125} \times \pi \approx 3.7$

=> Vậy lượng nước cần chuẩn bị gần bằng 3.7 lít

#5. Phân biệt định nghĩa mặt cầu và hình cầu

Chúng ta cần phân biệt định nghĩa của mặt cầu và hình cầu để sử dụng cho chính xác nhé.

• Mặt cầu là phần bên ngoài (vỏ) của hình cầu
• Hình cầu là … (xem hình trong phần #2)

Diện tích hình cầu, thể tích mặt cầu là những cụm từ không chính xác, chính xác phải là diện tích mặt cầu hoặc diện tích phần bên ngoài của hình cầu, thể tích hình cầu.

#6. Lời kết

Ngoài hình cầu ra thì các phần của hình cầu như hình quạt cầu, hình chỏm cầu, hình đới cầu và hình chêm cầu cũng có công thức tính diện tích và thể tích.

Tuy nhiên các hình này khá ít gặp và công thức tính cũng khá là phức tạp nên mình không hướng dẫn ở đây, nếu muốn các bạn có thể tìm hiểu thêm trên Wikipedia nhé. Vì thực tế trong chương trình học của các bạn cũng sẽ không gặp những hình này.

Trong bài viết này bạn chỉ cần nắm chắc cho mình kiến thức về mặt cầu và hình cầu, cũng như cách tính diện tích mặt cầu và cách tính thể tích hình cầu là ok lắm rồi.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Công thức tính DIỆN TÍCH TỨ GIÁC và CHU VI TỨ GIÁC
• Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com