Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Các công cụ tô màu trong GeoGebra chỉ cung cấp cho chúng ta các tính năng cơ bản. Nếu dùng nó thì bạn chỉ có thể tô màu cho các đối tượng như điểm, đường thẳng, cung tròn… mà thôi !
Vậy nên, để tô màu cho các đối tượng phức tạp hơn hoặc phần giao nhau của các đường tròn, các đồ thị thì công cụ tô màu mặc định không thể đáp ứng được.
Vậy giải pháp ở đây là gì?
Vâng, trong bài viết này mình sẽ hướng dẫn cho các bạn cách sử dụng công cụ Circumcircular Arc và lệnh IntegralBetween để giải quyết những vấn đề nan giải bên trên…
Mục Lục Nội Dung
- I. Cách tô màu cho điểm, đường thẳng trong GeoGebra
- II. Tô màu cho cung tròn, đường Ellipse, đường tròn, đa giác
- III. Tô màu cho phần giao nhau của các cung tròn, các đường tròn
- IV. Tô màu cho phần giao nhau của các đa giác trong GeoGebra
- V. Tô màu cho phần giao nhau của các đồ thị hàm số trong GeoGebra
- VI. Lời kết
I. Cách tô màu cho điểm, đường thẳng trong GeoGebra
Cách 1:
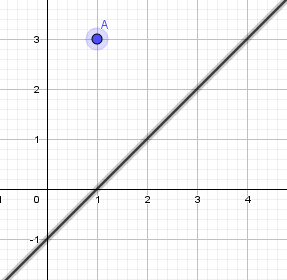
+ Bước 1: Bạn hãy chọn điểm, đường thẳng mà bạn cần tô màu..
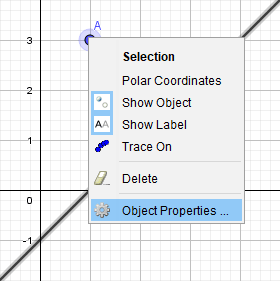
+ Bước 2: Nháy chuột phải => và chọn Object Properties …
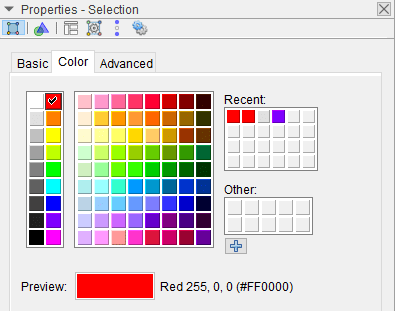
+ Bước 3: Hộp thoại Properties xuất hiện => chọn thẻ Color => chọn màu bạn muốn !
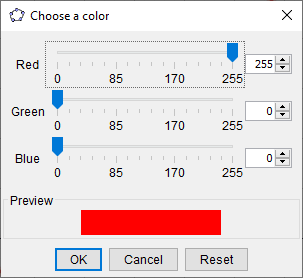
Nếu các màu có sẵn chưa đáp ứng được nhu cầu của bạn thì bạn có thể chọn vào biểu tượng “dấu cộng” để tùy chỉnh màu sắc theo ý thích của bạn nhé.
- Có thể bạn đang tìm: Bảng mã màu đầy đủ nhất cho bạn ! Cách lấy mã màu nhanh
Cách 2:
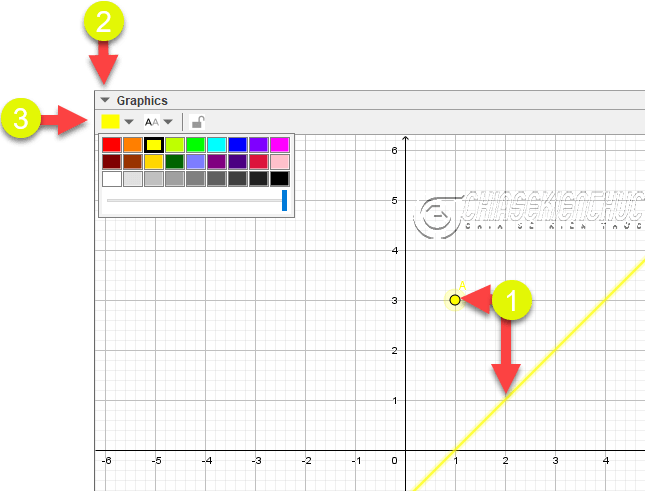
Chọn điểm, đường thẳng => sau đó chọn Graphics => chọn màu bạn thích.
II. Tô màu cho cung tròn, đường Ellipse, đường tròn, đa giác
Cách tô màu cho cung tròn, đường Ellipse, đường tròn và đa giác tương tự như cách tô màu cho điểm và đường thẳng.
Tuy nhiên, với các đối tượng thuộc nhóm này bạn còn có thể tô theo mẫu có sẵn hoặc tùy chỉnh Opacity. Trường hợp tô theo mẫu mình sẽ hướng dẫn dựa trên Propeties, còn tùy chỉnh Opacity sẽ là Graphics...
#1. Tô màu theo mẫu có sẵn
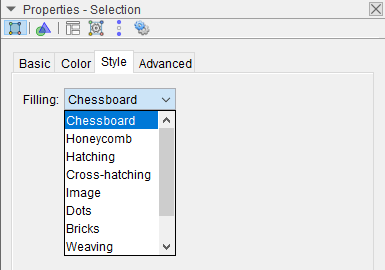
Trong hộp thoại Properties => bạn chọn thẻ Style => tại Filling bạn chọn một mẫu trong các mẫu mà phần mềm đã cung cấp..
Hình bên dưới theo thứ tự từ trái qua phải, từ trên xuống dưới là các mẫu: Chessboard, Honeycomb, Hatching, Cross-hatching, Image, Dots, Bricks và Weaving.
Trong đó, Hatching chính là mẫu mà mình đã sử dụng để biểu diễn tập hợp trên trục số..
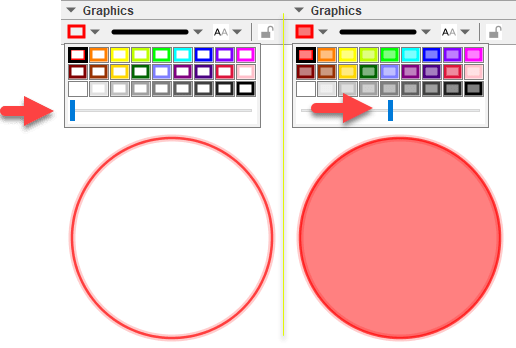
#2. Tùy chỉnh Opacity
Trong Graphics, bạn có thể kéo thả thanh trượt để thay đổi Opacity của đối tượng.
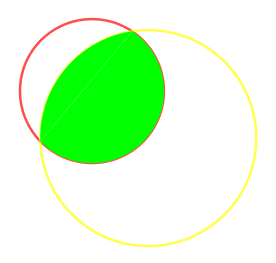
III. Tô màu cho phần giao nhau của các cung tròn, các đường tròn
Các trường hợp có thể xảy ra trong nhóm này là cung tròn và cung tròn; cung tròn và đường tròn; đường tròn và đường tròn.
Trong phạm vi của bài viết này mình sẽ hướng dẫn với các bạn thực hiện trường hợp thứ ba, đây cũng là trường hợp phức tạp nhất.
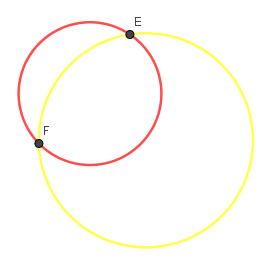
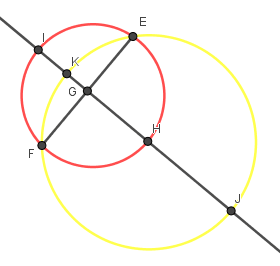
Ví dụ như ở đây chúng ta cần tô màu cho miền giao nhau của hai đường tròn (C) và (C’)
Các bước thực hiện:
| Bước 1: Dựng giao điểm của hai đường tròn.
|
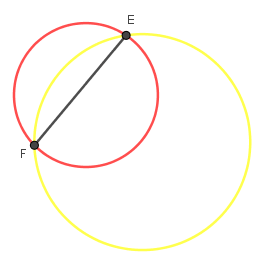
Bước 2: Dựng đoạn thẳng EF
|
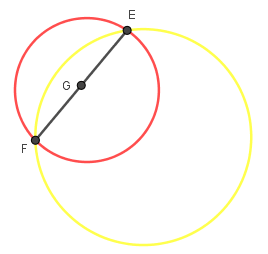
Bước 3: Dựng trung điểm của đoạn thẳng EF
|
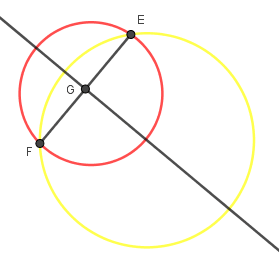
| Bước 4: Dựng đường trung trực của đoạn thẳng EF
|
Bước 5: Dựng giao điểm của đường trung trực và đường tròn
|
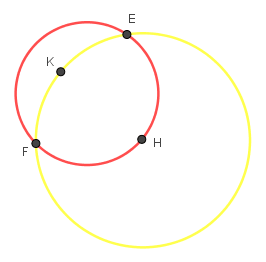
Bước 6: Ẩn các đối tượng phụ không cần thiết
|
| Bước 7: Dựng cung tròn đi qua ba điểm
|
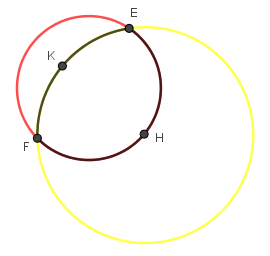
Bước 8: Tô màu cho hai cung tròn này và tùy chỉnh Opacity là 100%
|
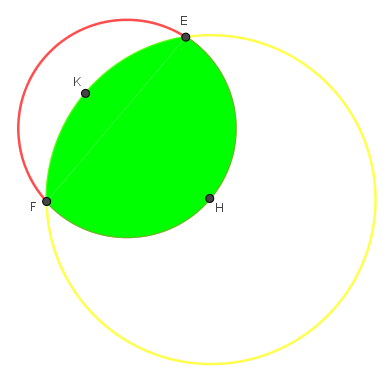
Bước 9: Ẩn các đối tượng phụ còn lại
|
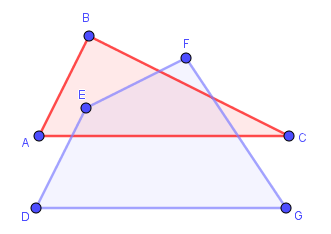
IV. Tô màu cho phần giao nhau của các đa giác trong GeoGebra
Ví dụ ở đây ta cần tô màu cho miền giao nhau của hai đa giác ABC vàDEFG
Các bước thực hiện:
+ Bước 1: Dựng giao điểm của hai đa giác
Chọn công cụ Intersect => chọn đa giác thứ nhất => rồi chọn đa giác thứ hai.
Hai đa giác này được mình dựng bằng công cụ Polygon, nếu bạn dựng bằng công cụ Segment thì bạn cần tạo giao điểm cho từ cặp đoạn thẳng.
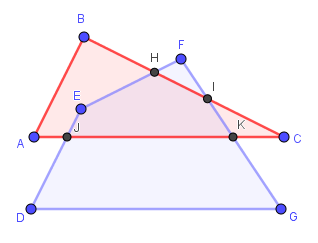
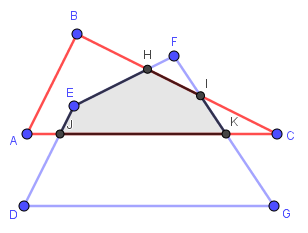
+ Bước 2: Tô màu cho miền giao nhau:
Chọn công cụ Polygon => chọn điểm E => lần lượt chọn điểm H, I, K, J và E
Khi sử dụng công cụ Polygon để dựng đa giác thì phần bên trong sẽ tự động được tô màu và màu mặc định là màu nâu.
V. Tô màu cho phần giao nhau của các đồ thị hàm số trong GeoGebra
Tô màu cho phần giao nhau của các đồ thị hàm số là một trong những công việc thường gặp khi biên soạn đề kiểm tra, hay là đề thi ở cấp THPT mà đặc biệt là ở lớp 12
Đồ thị thường gặp là các đồ thị của các hàm số như hàm nhị thức, hàm tam thức, hàm bậc ba, hàm bậc bốn, hàm phân thức, …
Ví dụ ở đây, ta cần tô màu cho phần giao nhau của hàm số f(x)=x-1 và h(x)=(x-1)3
Các bước thực hiện:
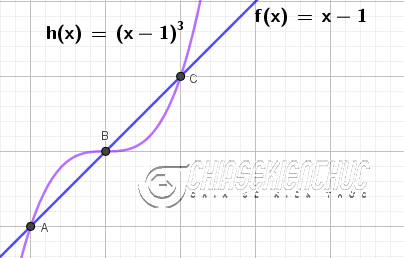
+ Bước 1: Dựng giao điểm của hai đồ thị.
Chọn công cụ Intersect => chọn đường đồ thị thứ nhất rồi chọn đồ thị thứ 2.
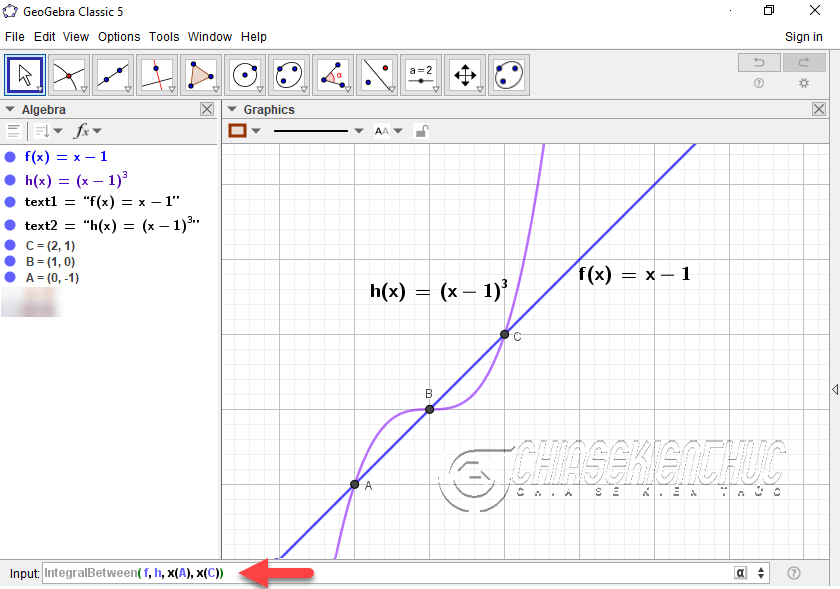
+ Bước 2: Sử dụng lệnh IntegralBetween:
Nhập lệnh IntegralBetween( f, h, x(A), x(C)) vào thanh Input => nhấn phím Enter
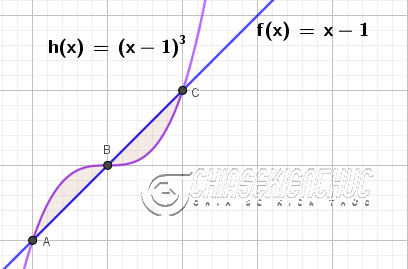
Kết quả sẽ như hình bên dưới:
Trường hợp bạn chỉ muốn tô một phần giao nhau (bên dưới hoặc bên trục hoàng) thì hai lệnh tô lần lượt là IntegralBetween( f, h, x(A), x(B)) và IntegralBetween( f, h, x(B), x(C))
VI. Lời kết
Trên đây là các trường hợp thường gặp trong thực tế khi sử dụng phân mềm GeoGebra để tô màu cho các đối tượng hình học. Tuy nhiên cũng có một số trường hợp ít gặp hơn mà mình chưa hướng dẫn.
Chẳng hạn như phần giao nhau của ba đối tượng trong cùng một nhóm, phần giao nhau của hai đối tượng đến từ hai nhóm khác nhau, phần giao nhau của hai Ellips, …
Khi gặp các trường hợp trên thì bạn cần linh động, vận dụng sáng tạo kiến thức thì mới có thể giải quyết được (“Từ từ rồi sẽ làm được”).
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Xem thêm các bài viết về GeoGebra !
