Xin chào tất cả các bạn, hôm này chúng ta sẽ cùng nhau tìm hiểu về cách vẽ các loại đa diện đều bằng GeoGebra (một phần mềm vẽ hình hình học động chuyên nghiệp).
Cụ thể thì chúng ta sẽ vẽ tứ diện đều, vẽ hình lập phương, vẽ bát diện đều, vẽ thập nhị diện đều và vẽ nhị thập diện đều.
Sau khi vẽ xong bạn có thể trình bày trực tiếp trên phần mềm hoặc xuất ra rồi chèn vào Word để soạn giáo án, đề kiểm tra…. hoặc chèn vào PowerPoint để trình chiếu trên máy chiếu.
Mục Lục Nội Dung
I. Đa diện đều là gì?
Đa diện đều là đa diện lồi có các tính chất …
- Mỗi mặt là một đa giác đều
pcạnh. - Mỗi đỉnh là đỉnh chung của đúng
qmặt.
Đa diện đều như vậy thì được gọi là đa diện đều loại {p; q}
Các nhà Toán học đã chứng minh được chỉ có đúng 5 loại đa diện đều là: tứ diện đều, lập phương, bát diện đều, thập nhị diện đều (12 mặt đều) và nhị thập diện đều (20 mặt đều).
II. Cách vẽ các đa diện đều bằng GeoGebra
Bước chung:
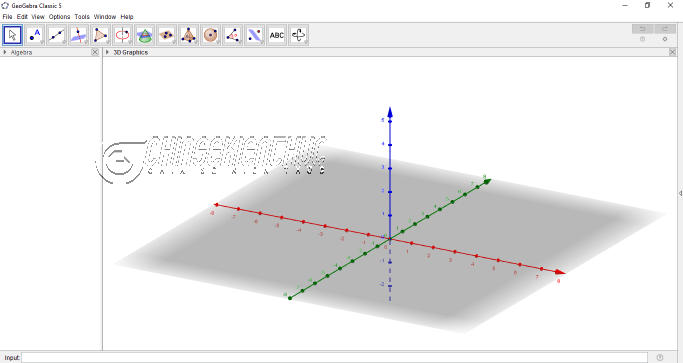
Nháy đúp chuột vào biểu tượng của phần mềm GeoGebra để khởi động phần mềm lên. Tiếp theo, sẽ có 2 cách cho bạn chọn lựa:
- Cách 1: Chọn View => chọn 3D Graphics => chọn View => chọn Graphics
- Cách 2: Nhấn tổ hợp phím Ctrl + Shift + 3 => nhấn tổ hợp phím Ctrl + Shift + 1
Kết quả chúng ta thu được giao diện làm việc như hình bên dưới …
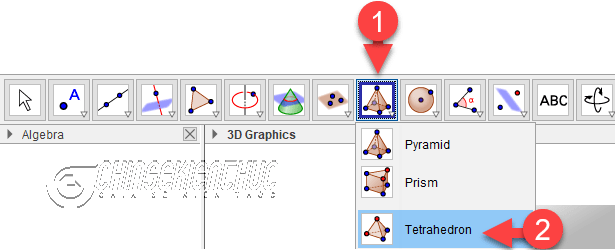
#1. Cách vẽ tứ diện đều bằng phần mềm GeoGebra
Bước 1. Chọn Pyramid => chọn Tetrahedron
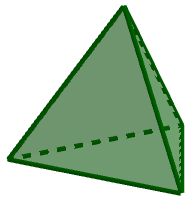
Bước 2. Nháy chuột trái để chọn vị trí của điểm thứ nhất => tiếp tục, nháy chuột trái để chọn vị trí của điểm thứ 2.
Ngay lập tức phần mềm sẽ dựng cho chúng ta một tứ diện đều với độ dài của mỗi cạnh bằng khoảng cách giữa hai điểm vừa dựng.
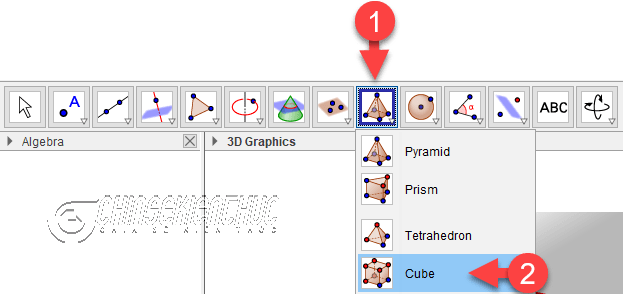
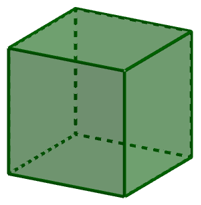
#2. Cách vẽ khối lập phương bằng phần mềm GeoGebra
Bước 1. Chọn Pyramid => chọn Cube
Bước 2. Nháy chuột trái để chọn vị trí của điểm thứ nhất => tiếp tục, nháy chuột trái để chọn vị trí của điểm thứ 2.
Ngay lập tức phần mềm sẽ dựng cho chúng ta một lập phương với độ dài của mỗi cạnh bằng khoảng cách giữa hai điểm vừa dựng. Rất đơn giản phải không ạ 🙂
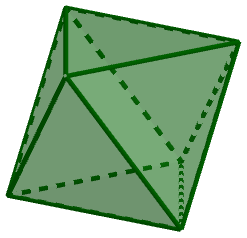
#3. Cách vẽ bát diện đều bằng phần mềm GeoGebra
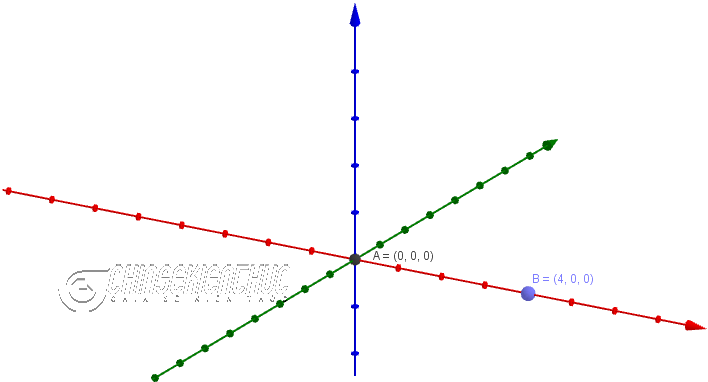
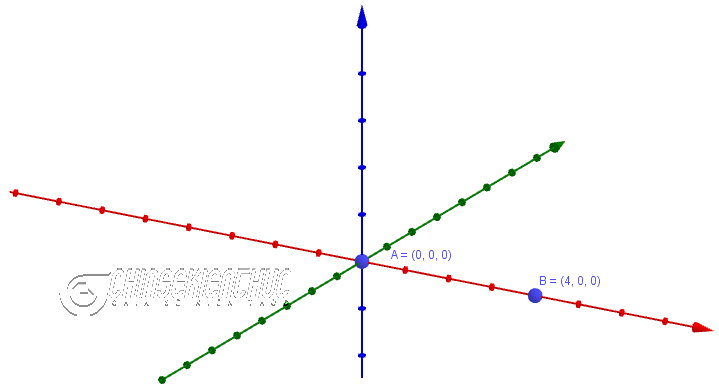
Bước 1. Chọn công cụ Point => nháy chuột vào không gian Oxyz để dựng hai điểm bất kì.
Ở đây mình sẽ dựng hai điểm A=(0; 0; 0) và B=(4; 0; 0)
Bước 2. Nhập lệnh Octahedron(A, B) vào thanh Input => nhấn phím Enter để thực hiện.
#4. Cách vẽ thập nhị diện đều
Bước 1 …
Cách 1: Thực hiện tương tự Bước 1 của mục #3 bên trên (Bát diện đều)
Cách 2:
- Nhập lệnh
A=(0,0,0)vào thanh Input => nhấn phímEnter - Nhập lệnh
B=(4,0,0)vào thanh Input => nhấn phímEnter
Bước 2. Nhập lệnh Dodecahedron(A, B) vào thanh Input => nhấn phím Enter
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
#5. Cách vẽ nhị thập diện đều
Bước 1. Thực hiện tương tự Bước 1 của mục #3 (Bát diện đều) HOẶC #4 (Thập nhị diện đều) bên trên.
Bước 2. Nhập lệnh Icosahedron(A, B) vào thanh Input => nhấn phím Enter
III. Một số chú ý khi vẽ hình
- Tùy chỉnh lại góc nhìn cho phù hợp, góc nhìn như sách giáo khoa là rất sư phạm.
- Nếu cần in ra (in trắng đen) thì bạn cần tùy chỉnh lại màu sắc (màu của các mặt nên là màu trắng).
IV. Lời kết
Như vậy là qua bài viết này chúng ta đã cùng nhau tìm hiểu xong về cách vẽ 5 loại đa diện đều trong không gian Oxyz bằng phần mềm GeoGebra rồi ha.
Cụ thể với phần mềm GeoGebra thì chúng ta có thể nhanh chóng vẽ được tứ diện đều, lập phương, bát diện đều, thập nhị diện đều và nhị thập diện đều.
Tuy nhiên, trong một số trường hợp đặc biệt, chúng ta cần vẽ các khối đa diện đều trên mặt phẳng Oxy thì làm như thế nào?
- Trường hợp 1: Vẽ bằng phần mềm GeoGbra xuất đa diện trong không gian Oxyz => chèn vào mặt phẳng Oxy => đồ theo hình mẫu vừa chèn.
- Trường hợp 2: Vẽ trên giấy / bằng tay rất khó vẽ được trừ khi bạn có hoa tay và có trí tưởng tượng tốt.
Okay, hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống







Các bài viết rất hữu ích với mình
Hướng dẫn mình cách trải hình trụ để xây dựng công thức tính điện tích và thể tích của hình trụ
Hướng dẫn mình cách tạo bảng nút điều khiển để hiển thị từng phần của hình