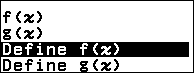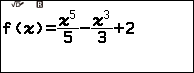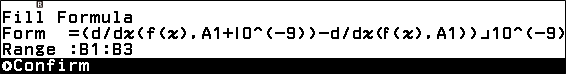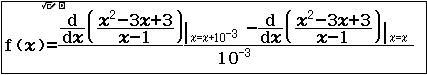Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Vâng, để có thể sử dụng máy tính CASIO để xác định nhanh cực trị của hàm số thì chúng ta cần tính được đạo hàm cấp hai tại nhiều điểm.
Tuy rằng chúng ta có thể sử dụng thủ thuật tính đạo hàm cấp hai tại một điểm để tính đạo hàm cấp hai tại nhiều điểm NHƯNG sẽ tốn khá nhiều thời gian.
Biết được khó khăn trên nên hôm nay, mình sẽ hướng dẫn cho các bạn cách sử dụng máy tính CASIO để tính đạo hàm cấp hai tại nhiều điểm một cách nhanh chóng hơn.
Mục Lục Nội Dung
#1. Thủ thuật này dựa trên cơ sở nào?
Mặc dù máy tính CASIO vẫn chưa hỗ trợ chúng ta tính trực tiếp đạo hàm cấp hai tại một điểm.
Tuy nhiên, chúng ta có vẫn thể tính được một cách gián tiếp nhờ vào định nghĩa $f”(x_0)=\lim_{h \rightarrow 0} \frac{f'(x_0+h)-f'(x_0)}{h}$
Chú ý.
Giá trị tính bằng thủ thuật này là một giá trị gần đúng.
#2. Các bước tính đạo hàm cấp 2 tại nhiều điểm
Có hai tính năng giúp chúng ta tính nhanh đạo hàm cấp hai tại nhiều điểm là tính năng bảng tính Spreadsheet và tính năng bảng giá trị Table trên máy tính Casio.
Cách 1. Sử dụng tính năng bảng tính Spreadsheet
Bước 1. Gán hàm số cần tính đạo hàm cấp hai vào hàm nhớ f(x)
Bước 2. Mở bảng tính Spreadsheet
Bước 3. Nhập các điểm cần tính đạo hàm cấp hai vào các ô A1, A2, A3, …
Bước 4. Chọn ô B1 rồi sử dụng tính năng Fill Formula với Form là (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1))⨼10^(-9) và Range là B1:Bn
Chú ý.
n là bao nhiêu phụ thuộc vào số lượng điểm cần tính các bạn nhé.
Bước 5. Quan sát cột B
Những giá trị ở cột B chính là giá trị gần đúng của đạo hàm cấp hai của hàm số f(x) tại các điểm ở cột A
Cách 2. Sử dụng tính năng bảng giá trị Table
Bước 1. Mở tính năng tạo bảng giá trị Table
Bước 2. Nhập f(x) là $\frac{\frac{d}{dx}(f(x))|_{x=x+10^{-9}}-\frac{d}{dx}(f(x))|_{x=x}}{10^{-9}}$
Bước 3. Giữ nguyên các giá trị Start=1, End=5, Step=1
Bước 4. Nhập các giá trị cần tính đạo hàm cấp hai vào cột x
#3. Cách tính đạo hàm cấp hai trên máy Casio 880 BTG
Ví dụ 1. Tính đạo hàm cấp hai của hàm số $f(x)=\frac{x^5}{5}-\frac{x^3}{3}+2$ tại các điểm -1, 0, 1
Bước 1. Gán hàm số $\frac{x^5}{5}-\frac{x^3}{3}+2$ vào hàm nhớ f(x)
Bước 1.1. Nhấn phím FUNCTION => chọn Define f(x) => nhấn phím OK
Bước 1.2. Nhập hàm số $\frac{x^5}{5}-\frac{x^3}{3}+2$ => nhấn phím EXE
Bước 2. Mở bảng tính Spreadsheet
Nhấn phím HOME => chọn Spreadsheet => nhấn phím OK
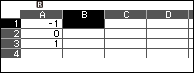
Bước 3. Nhập -1, 0, 1 vào các ô A1, A2, A3
Nhập -1 => nhấn phím EXE => nhập 0 => nhấn phím EXE => nhập 1 => nhấn phím EXE
Bước 4. Chọn ô B1 rồi sử dụng tính năng Fill Formula với Form là (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1))⨼10^(-9) và Range là B1:B3
Bước 4.1. Chọn ô B1
Bước 4.2. Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK
Bước 4.3. Nhập (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1))⨼10^(-9) => nhấn phím EXE => nhập B1:B3 => nhấn phím EXE => nhấn phím EXE
Gợi ý:
- Nhấn
để nhập d/dx - Nhấn
để nhập f - Có thể thay $10^{-9}$ bằng $10^{-6}$ hoặc $10^{-3}$
để nhập d/dx
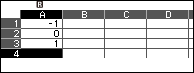
để nhập fBước 5. Quan sát cột B
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Những giá trị ở cột B chính là giá trị gần đúng của đạo hàm cấp hai của hàm số f(x) tại các điểm ở cột A
Vậy đạo hàm cấp hai của hàm số đã cho tại các điểm -1, 0, 1 lần lượt là -2, 0, 2
Chú ý.
Việc nhập trực tiếp (d/dx(f(x),A1+10^(-9))-d/dx(f(x),A1))⨼10^(-9) khá phức tạp nên trong Video hướng dẫn mình đã tách ra từng thành phần để đơn giản hơn.
Xem video hướng dẫn thực hiện trên Casio 880 BTG
#4. Cách tính đạo hàm cấp 2 trên máy fx 580 VNX
Ví dụ 2. Tính đạo hàm cấp hai của hàm số $f(x)=\frac{x^2-3x+3}{x-1}$ tại các điểm 0, 2
Bước 1. Mở tính năng tạo bảng giá trị Table
Nhấn phím MENU => chọn Table => nhấn phím =
Bước 2. Nhập f(x) là $\frac{\frac{d}{dx}(\frac{x^2-3x+3}{x-1})|_{x=x+10^{-3}}-\frac{d}{dx}(\frac{x^2-3x+3}{x-1})|_{x=x}}{10^{-3}}$ => nhấn phím =
Mặc dù $10^{-9}$ sẽ cho kết quả chính xác hơn $10^{-6}$ và $10^{-3}$ nhưng vì chúng ta đang thực hành trên fx 580 VN X (chỉ nhớ được 15 chữ số) nên phương án an toàn là $10^{-3}$
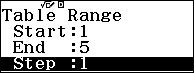
Bước 3. Giữ nguyên các giá trị Start=1, End=5, Step=1
Nhấn phím = => nhấn phím =
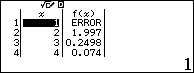
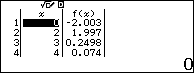
Bước 4. Nhập các giá trị cần tính đạo hàm cấp hai vào cột x
Nhập 0 => nhấn phím =
Vậy đạo hàm cấp hai của hàm số đã cho tại các điểm 0 và 2 lần lượt là -2 và 2
Xem video hướng dẫn thực hiện trên Casio 580 VNX
#5. Gợi ý cách chọn $10^{-9}$ hoặc $10^{-6}$ hoặc $10^{-3}$
Mặc định chọn $10^{-9}$
Nếu kết quả bằng 0 thì nên kiểm tra lại với $10^{-6}$ hoặc $10^{-3}$
Nếu xuất hiện thông báo hết thời gian Time Out thì thử lại với $10^{-6}$ hoặc $10^{-3}$
#6. Lời kết
Chúng ta thường phát sinh nhu cầu tính đạo hàm cấp hai tại nhiều điểm khi cần xác định cực trị của hàm số.
Lúc này, việc áp dụng thủ thuật CASIO vừa được trình bày bên trên sẽ gián tiếp giúp chúng ta xác định nhanh cực trị của một hàm số bất kì.
Rát hay đúng không nào 🙂 Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.
Đọc thêm:
- Cách tính đạo hàm cấp hai và cấp cao của một hàm số
- Cách tìm cực trị của hàm số bằng máy tính Casio 580 & 880
- Cách tìm cực trị của hàm số đa thức (bậc 2 và bậc 3)
- Tổng hợp công thức tính đạo hàm của các hàm số thường gặp
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
