Xin chào tất cả các bạn !
Trong bài viết này các bạn sẽ được cung cấp các công thức lượng giác đáng nhớ nhất trong chương trình Toán học Trung học.
Những công thức này chính là chìa khóa giúp các bạn tính được:
Giá trị lượng giác của một góc (không sử dụng máy tính cầm tay), chứng minh được một biểu thức lượng giác, giải phương trình lượng giác, cũng như hệ phương trình lượng giác, …
Mục Lục Nội Dung
- #0. Các công thức lượng giác cơ bản
- #1. Công thức cộng
- #2. Công thức nhân đôi
- #3. Công thức nhân ba
- #4. Công thức nhấn bốn
- #5. Công thức hạ bậc
- #6. Công thức biến đổi tích thành tổng
- #7. Công thức biến đổi tổng thành tích
- #8. Biến đổi $\tan \frac{\alpha}{2}=t$
- #9. Công thức biến đổi một số biểu thức đặc biệt thành tích
- #10. Công thức các cung liên kết trên đường tròn lượng giác
- #11. Bảng giá trị lượng giác một số góc đặc biệt
- #12. Lời kết
#0. Các công thức lượng giác cơ bản
- $\tan x=\frac{sin x}{cos x}$
- $\cot x=\frac{cos x}{sin x}$
- $\sin ^2 x + \cos ^2 x = 1$
- $\tan x \cot x = 1 ( x \neq k \frac{\pi}{2}, k \in Z)$
- $1 + tan ^2 x =\frac{1}{cos^2 x} ( x \neq \frac{\pi}{2} + k\pi, k \in Z)$
- $1 + cot ^2 x=\frac{1}{sin^2 x} ( x \neq k\pi, k \in Z)$
#1. Công thức cộng
Với mọi $\alpha$, $\beta$, chúng ta luôn có các công thức sau đối với $\cos$, $\sin$
- $\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$
- $\cos (\alpha+\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$
- $\sin (\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$
- $\sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$
Mẹo nhớ công thức: Sin thì sin cos cos sin, còn Cos thì cos cos sin sin (dấu trừ)
Có thơ luôn cho các bạn đây 🙂
Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng
Sin thì giữ dấu xin chàng nhớ cho !
Với $\alpha$, $\beta$ làm cho các công thức có nghĩa thì chúng ta có các công thức đối với $\tan$ như sau:
- $\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}$
- $\tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}$
Mẹo nhớ công thức: Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.
#2. Công thức nhân đôi
Nếu đặt $\alpha=\beta$ và thay vào các công thức cộng thì chúng ta sẽ được các công mới.
Các công thức mới được gọi là các công thức nhân đôi:
- $\sin 2 \alpha=2 \sin \alpha \cos \alpha$
- $\cos 2 \alpha=\cos ^2 \alpha-\sin ^2 \alpha=2 \cos ^2 \alpha-1=1-2 \sin ^2 \alpha$
Với $\alpha \neq \frac{\pi}{2}+k\pi, \alpha \neq \frac{\pi}{4}+k \frac{\pi}{2}, k \in Z$ chúng ta có thêm công thức $\tan 2 \alpha=\frac{2 \tan \alpha}{1-\tan ^2 \alpha}$
Mẹo nhớ:
Sin gấp đôi = 2 sin cos
Cos gấp đôi = bình cos trừ bình sin= trừ 1 cộng hai bình cos
= cộng 1 trừ hai bình sin
#3. Công thức nhân ba
- $\sin3 \alpha=3 \sin \alpha-4 \sin^3 \alpha$
- $\cos 3 \alpha=4 \cos^3 \alpha-3 \cos \alpha$
- $\tan 3 \alpha=\frac{3 \tan \alpha-\tan^3 \alpha}{1-3 \tan^2 \alpha}$
#4. Công thức nhấn bốn
- sin4a = 4.sina.cos3a – 4.cosa.sin3a
- cos4a = 8.cos4a – 8.cos2a + 1
- Hoặc cos4a = 8.sin4a – 8.sin2a + 1
#5. Công thức hạ bậc
Các công thức hạ bậc cho phép chúng ta biến đổi các biểu thức $\sin^2 \alpha, \cos^2 \alpha, \tan^2 \alpha$ thành các biểu thức $\cos2 \alpha$
- $\cos ^2 \alpha=\frac{1+\cos 2 \alpha}{2}$
- $\sin ^2 \alpha=\frac{1-\cos 2 \alpha}{2}$
- $\tan ^2 \alpha=\frac{1-\cos 2 \alpha}{1+\cos 2 \alpha}$
#6. Công thức biến đổi tích thành tổng
Biến đổi sơ cấp các công thức cộng chúng ta sẽ dễ dàng thu được các công thức biến đổi tích thành tổng.
- $\cos \alpha \cos \beta=\frac{1}{2}[\cos (\alpha-\beta)+\cos (\alpha+\beta)]$
- $\sin \alpha \sin \beta=\frac{1}{2}[\cos (\alpha-\beta)-\cos (\alpha+\beta)]$
- $\sin \alpha \cos \beta=\frac{1}{2}[\sin (\alpha-\beta)+\sin (\alpha+\beta)]$
#7. Công thức biến đổi tổng thành tích
Nếu chúng ta đặt $\alpha + \beta=x$, $\alpha – \beta=y$ tức $\alpha=\frac{x+y}{2}$, $\beta=\frac{x-y}{2}$ và thay vào các công thức biến đổi tích thành tổng thì chúng ta sẽ suy ra được các công biến đổi tổng thành tích.
- $\cos x+\cos y=2 \cos \frac{x+y}{2} \cos \frac{x-y}{2}$
- $\cos x-\cos y=-2 \sin \frac{x+y}{2} \sin \frac{x-y}{2}$
- $\sin x+\sin y=2 \sin \frac{x+y}{2} \cos \frac{x-y}{2}$
- $\sin x-\sin y=2 \cos \frac{x+y}{2} \sin \frac{x-y}{2}$
Mẹo nhớ:
Cos cộng cos bằng 2 cos cos
Cos trừ cos bằng – 2 sin sin
Sin cộng sin bằng 2 sin sin
Sin trừ sin bằng 2 cos sin.
#8. Biến đổi $\tan \frac{\alpha}{2}=t$
- $\sin \alpha=\frac{2t}{1+t^2}$
- $\cos \alpha=\frac{1-t^2}{1+t^2}$
- $\tan \alpha=\frac{2t}{1-t^2}$
#9. Công thức biến đổi một số biểu thức đặc biệt thành tích
- $1+\cos \alpha=2 \cos^2 \frac{\alpha}{2}$
- $1-\cos \alpha=2 \sin^2 \frac{\alpha}{2}$
- $1+\sin \alpha=2 \cos^2 (\frac{\pi}{4}-\frac{\alpha}{2})$
- $1-\sin \alpha=2 \sin^2 (\frac{\pi}{4}-\frac{\alpha}{2})$
- $\cos \alpha \pm \sin \alpha=\sqrt{2}\cos(\frac{\pi}{4} \mp \alpha)=\sqrt{2}(\frac{\pi}{4} \pm \alpha)$
Với $\tan \varphi=\frac{a}{b}, a \neq 0, b \neq 0$ chúng ta có thêm công thức $a\cos \alpha+b \sin \alpha=\sqrt{a^2+b^2} \cos (\varphi-\alpha)=\sqrt{a^2+b^2} \sin (\varphi+\alpha)$
#10. Công thức các cung liên kết trên đường tròn lượng giác
Vâng, để việc tính toán trở nên đơn giản hơn thì bạn nên ghi nhớ giá trị của các cung đặc biệt. “Cos đối, Sin bù, phụ chéo, khác pi Tan”.
Cụ thể hơn thì cosin của 2 góc đối nhau sẽ có giá trị bằng nhau, còn Sin của 2 góc bù nhau cũng bằng nhau, 2 góc phụ nhau thì sẽ cho giá trị là:
Sin góc này = Cos góc kia , Tan góc này= Costan góc kia, Tan của 2 góc hơn kém nhau một giá trị pi thì sẽ bằng nhau.
Sin= đối/ huyền
Cos= kề/ huyền
Tan= đối/ kề
Cot= kề/ huyền
10.1. Hai góc đối nhau:
- cos (-x) = cos x
- sin (-x) = -sin x
- tan (-x) = -tan x
- cot (-x) = -cot x
10.2. Hai góc bù nhau:
- sin (π – x) = sin x
- cos (π – x) = -cos x
- tan (π – x) = -tan x
- cot (π – x) = -cot x
10.3 Hai góc phụ nhau:
- sin (π/2 – x) = cos x
- cos (π/2 – x) = sin x
- tan (π/2 – x) = cot x
- cot (π/2 – x) = tan x
10.4. Hai góc hơn kém π:
- sin (π + x) = -sin x
- cos (π + x) = -cos x
- tan (π + x) = tan x
- cot (π + x) = cot x
10.5. Hai góc hơn kém π/2:
- sin (π/2 + x) = cos x
- cos (π/2 + x) = -sin x
- tan (π/2 + x) = -cot x
- cot (π/2 + x) = -tan x
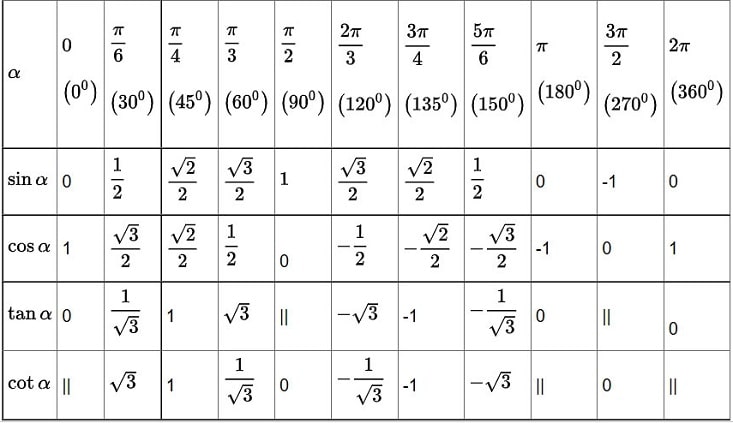
#11. Bảng giá trị lượng giác một số góc đặc biệt
#12. Lời kết
Việc nhớ và sử dụng linh hoạt các công thức lượng giác mà mình vừa trình bày bên trên không phải chuyện đơn giản, mà chắc chắn nó sẽ tốn khá nhiều thời gian và công sức của các bạn.
Giải pháp được nhiều người sử dụng là đọc đến đâu áp dụng ngay đến đó, giải pháp này không chỉ giúp bạn khắc sâu công thức mà còn giúp bạn biết cách sử dụng công thức một cách linh hoạt hơn.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Cách giải phương trình lượng giác (có nhiều ví dụ)
- MathType: Tạo ký hiệu song song, đồng dạng, cung lượng giác..
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống