Cách giải phương trình mũ (2 dạng thường gặp nhất)

Bạn đã biết cách giải phương trình mũ chưa? Phương trình có dạng $a^x=m$ với $a, m$ là những số thực cho trước và $0<a \neq 1$ được gọi là phương trình mũ.

Hôm nay chúng ta sẽ cùng nhau tìm hiểu về cách giải phương trình mũ trên và hai dạng phương trình mũ thường gặp khác…

#1. Phương trình mũ cơ bản

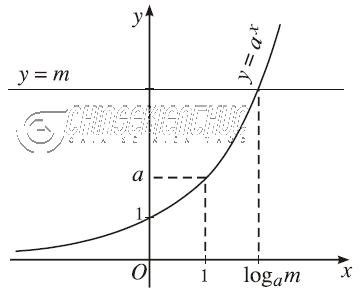
Phương trình mũ cơ bản có dạng $a^x=m$ với $a, m$ là những số thực cho trước và $0<a \neq 1$

Việc giải phương trình $a^x=m$ rất đơn giản, bạn chỉ cần xem xét giá trị của $m$ là xong.

• Trường hợp 1. Nếu $m \leq 0$ thì phương trình $a^x=m$ vô nghiệm.
• Trường hợp 2. Nếu $m>0$ thì phương trình $a^x=m$ có một nghiệm duy nhất là $x=\log_a m$.

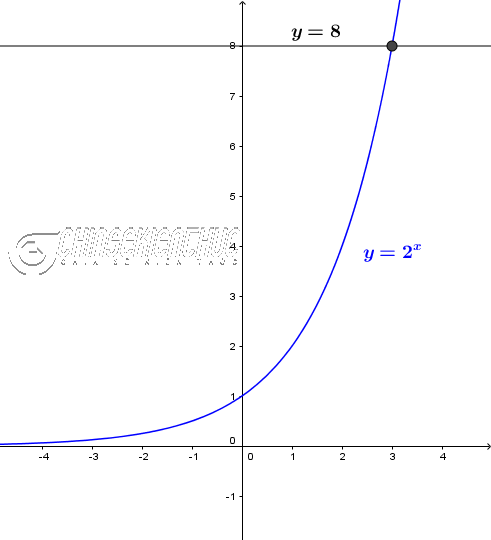
Ví dụ 1. Giải phương trình $2^x=8$

Lời giải:

$2^x=8 \Leftrightarrow x=\log_2 8 \Leftrightarrow x=3$

Vậy tập nghiệm của phương trình đã cho là $\{3\}$

#2. Cách giải phương trình mũ 

Dưới đây là hai dạng phương trình mũ thường gặp nhất, cũng là dạng phương trình mũ dễ giải nhất.

1. Phương trình mũ có thể đưa về cùng cơ số.
2. Phương trình mũ có thể giải được bằng phương pháp đặt ẩn phụ.

2.1. Đưa về cùng cơ số

Trước hết, chúng ta thừa nhận mệnh đề tương đương $a^{f(x)}=b^{g(x)} \Leftrightarrow f(x)=g(x)$

Mệnh đề trên cho phép chúng ta giải các dạng phương trình mũ bằng cách đưa các lũy thừa trong phương trình về lũy thừa với cùng một cơ số.

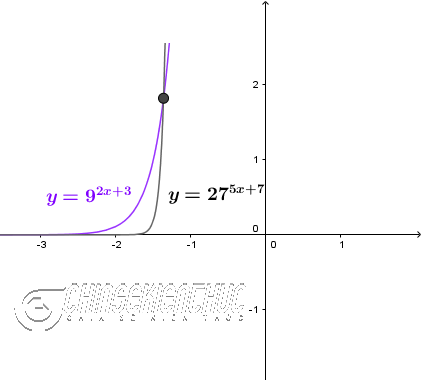
Ví dụ 2. Giải phương trình $9^{2x+3}=27^{5x+7}$ $(*)$

Gợi ý:

Đưa hai vế của phương trình về lũy thừa có cùng cơ số $3$

Lời giải:

Dễ thấy $9^{2x+3}=3^{2(2x+3)}$ và $27^{5x+7}=3^{3(5x+7)}$

$(*) \Leftrightarrow 3^{2(2x+3)}=3^{3(5x+7)} \Leftrightarrow 2(2x+3)=3(5x+7) \Leftrightarrow -11x-15=0 \Leftrightarrow x=-\frac{15}{11}$

Vậy tập nghiệm của phương trình đã cho là $\left\{-\frac{15}{11}\right\}$

2.2. Đặt ẩn phụ

Bằng cách đặt ẩn phụ thích hợp chúng ta có thể chuyển từ việc giải một phương trình mũ phức tạp sang việc giải các phương trình mũ đơn giản.

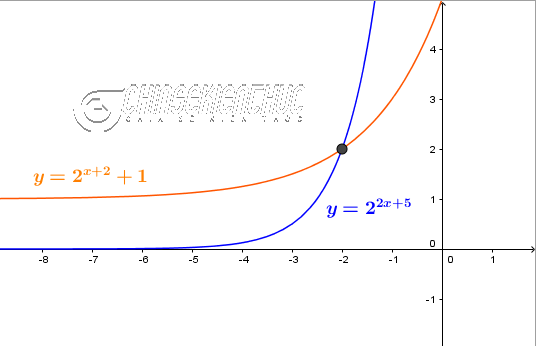
Ví dụ 3. Giải phương trình $2^{2x+5}=2^{x+2}+1$ $(*)$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Gợi ý:
Áp dụng các công thức $a^{m+n}=a^m.a^n$, $a^{m.n}=(a^n)^m$, biến đổi phương trình đã cho thành phương trình có thể đặt ẩn phụ được

Lời giải:

Dễ thấy $2^{2x+5}=2.2^{2x+4}=2.2^{2(x+2)}=2.(2^{x+2})^2$

$(*) \Leftrightarrow 2.(2^{x+2})^2=2^{x+2}+1 \Leftrightarrow 2.(2^{x+2})^2-2^{x+2}-1=0$

Đặt $t=2^{x+2}$, điều kiện $t>0$

$2t^2-t-1=0 \Leftrightarrow \left[\begin{array}{l} t = 1 \\ t = -\frac{1}{2} \end{array}\right.$

$t = -\frac{1}{2}$ bị loại do không thỏa mãn điều kiện

Với $t=1$ ta được phương trình $1=2^{x+2} \Leftrightarrow 2^0=2^{x+2} \Leftrightarrow0=x+2 \Leftrightarrow x=-2$

Vậy => tập nghiệm của phương trình là $\{-2\}$

#3. Lời kết

Trong Toán học, ngoài hai dạng phương trình mũ trên còn khá nhiều dạng phương trình mũ khác.

Nếu gặp phải các trường hợp khác thì các bạn nên ưu tiên sử dụng các công thức $a^{m+n}=a^m.a^n$, $a^{m.n}=(a^n)^m$, … để biến đổi chúng về hai dạng quen thuộc bên trên.

Ngoài ra thì các bạn cũng nên tham khảo thêm:

• Phương pháp Logarit hóa.
• Phương pháp sử dụng tính đồng biến, nghịch biến của hàm số.

… để có nhiều phương pháp hơn, từ đó giải được nhiều dạng phương trình mũ hơn các bạn nhé. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn