Những quy tắc tính xác suất nhất định bạn phải biết

Xin chào tất cả các bạn !

Xác suất là một trong những mạch kiến thức quan trọng trong Chương trình Giáo dục Phổ thông.

Mạch kiến thức này khá khó, khó với cả học sinh và cả giáo viên, học sinh thì khó hiểu, mà giáo viên thì khó dạy, khó truyền đạt kiến thức.

Vậy nên hôm nay mình sẽ cố gắng hệ thống lại một cách chính xác và đầy đủ các quy tắc tính xác suất thường sử dụng nhất.

Hi vọng qua bài viết này bạn sẽ nắm được một số kiến thức cơ bản, mang tính chất nền tảng, từ đó dễ dàng tiếp cận được các kiến thức nâng cao.

I. Phép thử và biến cố

#1. Phép thử là gì?

Một thí nghiệm, một phép đo, hay một sự quan sát một hiện tượng nào đó, … được gọi là một phép thử.

Tập hợp tất cả các kết quả có thể xảy ra của phép thử được gọi là không gian mẫu của phép thử.

Người ta thường ký hiệu không gian mẫu của phép thử là $\Omega$

Trong phạm vi ngắn gọn của bài viết này chúng ta chỉ xét các phép thử có không gian mẫu $\Omega$ là một tập hữu hạn nha các bạn.

#2. Biến cố là gì?

Biến cố là một tập con của không gian mẫu.

• Tập $\emptyset$ được gọi là biến cố không thể
• Tập $\Omega$ được gọi là biến cố chắn chắn

#3. Các phép toán trên các biến cố

Cho $A$ và $B$ là các biến cố liên quan đến phép thử $T$

Lúc này …

• Biến cố $\bar{A}=\Omega$ \ $A$ được gọi là biến cố đối của biến cố $A$. Dễ thấy $\bar{A}$ xảy ra khi và chỉ khi $A$ không xảy ra. $A$ và $B$ đối nhau khi và chỉ khi $\bar{A}=B$
• Biến cố $A \cup B$ được gọi là hợp của biến cố $A$ và biến cố $B$. Biến cố $A \cup B$ xảy ra khi và chỉ khi $A$ hoặc $B$ xảy ra.
• Biến cố $A \cap B$ được gọi là giao của biến cố $A$ và biến cố $B$. Biến cố $A \cap B$ xảy ra khi và chỉ khi $A$ và $B$ cùng xảy ra.
• Nếu $A \cap B = \emptyset$ thì $A$ và $B$ được gọi là hai biến cố xung khắc, nói cách khác $A$ hoặc $B$ xảy ra khi và chỉ khi $B$ hoặc $A$ không xảy ra.

II. Xác suất của biến cố

#1. Xác suất là gì?

Giả sử phép thử $T$ có không gian mẫu $\Omega$ là một tập hợp hữu hạn và các kết quả của $T$ là đồng khả năng xảy ra.

$A$ là một biến cố liên quan đến một phép thử $T$ và $n(A)$ là số phần tử của $A$

$n(A)$ được gọi là số kết quả thuận lợi cho $A$ và $n(\Omega)$ là số phần tử của $\Omega$

Lúc bấy giờ chúng ta gọi tỉ số $\frac{n(A)}{n(\Omega)}$ là xác suất của biến cố $A$

Người ta thường ký hiệu xác suất của biến cố $A$ là $P(A)$

#2. Các tính chất của xác suất

• $P(\Omega)=1$, $P(\emptyset)=0$
• $0 \leq P(A) \leq 1$ với mọi biến cố A
• $P(\bar{A})=1-P(A)$ với mọi biến cố A
• Nếu $A$ và $B$ là hai biến cố xung khắc cùng liên quan đến phép thử thì $P(A \cup B)=P(A)+P(B)$
• Nếu $A$ và $B$ là hai biến cố độc lập (sự xảy ra của một trong hai biến cố không ảnh hưởng đến xác suất xảy ra của biến cố kia) thì $P(A \cap B)=P(A \dot{} B)=P(A) \dot{} P(B)$
• $P(\overline{A \cup B})=P(\bar{A} \cap \bar{B})$, $P(\overline{A \cap B})=P(\bar{A} \cup \bar{B})$

III. Sử dụng máy tính CASIO FX 880 BTG tính xác suất

Máy tính cầm tay CASIO FX 880 BTG có thể tính được một số bài toán xác suất tương tự các bài toán được liệt kê bên dưới.

NOTE:
Link mua máy tính Casio FX 880 BTG

Sử dụng tính năng Dice Roll chúng ta sẽ giải quyết được bài toán “gieo đồng thời 3 con xúc xắc, tính xác suất để tổng số chấm xuất hiện trên 3 con bằng 10”

Sử dụng tính năng Coin Toss chúng ta sẽ giải quyết được bài toán “tung 3 đồng xu cân đối và đồng chất, tính xác suất để có đúng 2 đồng xu xuất hiện mặt sấp”

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

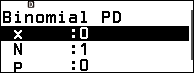
Sử dụng tính năng Binomial PD và Binomial PD để tính chính xác phân phối nhị thức và tích lũy nhị thức.

I.V Lời kết

Các quy tắc tính xác suất được trình bày trong bài viết này là chìa khóa để chúng ta có thể giải được / tính được các bài toán xác suất.

Đây cũng là các kiến thức nhập môn Lý thuyết xác suất, môn học đã trở thành một nhánh rất quan trọng trong Toán học.

Có nhiều ứng dụng trong nhiều lĩnh vực của khoa học tự nhiên, khoa học xã hội, công nghệ, kinh tế, y học, sinh học, … Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé.

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn