Tập xác định, tính chẵn lẻ, chu kỳ và đồ thị của hàm số lượng giác

Xin chào tất cả các bạn !

Các hàm số lượng giác $y=\sin x$, $y=\cos x$, $y=\tan x$, $y=\cot x$ thường được sử dụng để mô tả các hiện tượng thay đổi một cách tuần hoàn trong thực tiễn.

Vậy nên trong bài viết ngày hôm nay, chúng ta sẽ cùng nhau tìm hiểu về các hàm số lượng giác $y=\sin x, y=\cos x, y=\tan x, y=\cot x$

Cụ thể là tìm tập xác định, tập giá trị, tính chẵn lẻ, tính tuần hoàn (chu kỳ) và đồ thị của hàm số lượng giác nhé.

#1. Hàm số lượng giác sin

Quy tắc đặt tương ứng mỗi số thực $x$ với $\sin$ của góc lượng giác có số đo rađian bằng $x$ được gọi là hàm số $\sin$

Hàm số lượng giác $y=\sin x$ có tập xác định là $R$ và tập giá trị là $[-1, 1]$

Hàm số $y=\sin x$ là hàm lẻ vì $\sin (-x)=-\sin(x)$ với mọi số thực $x$

Hàm số $y=\sin x$ là hàm tuần hoàn với chu kỳ $2\pi$

Các giá trị đặc biệt của hàm số $y=\sin x$

• $\sin x=0$ khi $x=k\pi$ với $k$ là một số nguyên bất kỳ
• $\sin x=1$ khi $x=\frac{\pi}{2}+k2\pi$ với $k$ là một số nguyên bất kỳ
• $\sin x=-1$ khi $x=-\frac{\pi}{2}+k2\pi$ với $k$ là một số nguyên bất kỳ

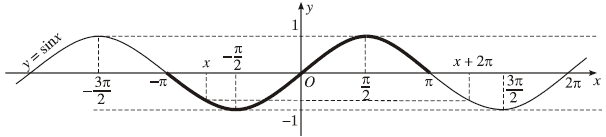
Đồ thị hàm số $y=\sin x$

#2. Hàm số lượng giác cos

Quy tắc đặt tương ứng mỗi số thực $x$ với $\cos$ của góc lượng giác có số đo rađian bằng $x$ được gọi là hàm số $\cos$

Hàm số $y=\cos x$ có tập xác định là $R$ và tập giá trị là $[-1, 1]$

Hàm số $y=\cos x$ là hàm chẵn vì $\cos (-x)=\cos(x)$ với mọi số thực $x$

Hàm số $y=\cos x$ là hàm tuần hoàn với chu kỳ $2\pi$

Các giá trị đặc biệt của hàm số $y=\cos x$:

• $\cos x=0$ khi $x=\frac{\pi}{2}+k\pi$ với $k$ là một số nguyên bất kỳ
• $\cos x=1$ khi $x=k2\pi$ với $k$ là một số nguyên bất kỳ
• $\cos x=-1$ khi $x=-\pi+k2\pi$ với $k$ là một số nguyên bất kỳ

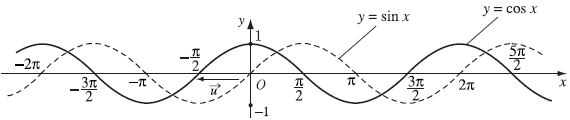
Đồ thị hàm số $y=\cos x$

#3. Hàm số lượng giác tan

Quy tắc đặt tương ứng mỗi số $x \in D=\mathbb{R}$ \ $\left\{\frac{\pi}{2}+k \pi \mid k \in \mathbb{Z}\right\}$ với số thực $\tan x=\frac{\sin x}{\cos x}$ được gọi là hàm số $\tan$

Hàm số $y=\tan x=\frac{\sin x}{\cos x}$ có tập xác định là $\mathbb{R}$ \ $\left\{\frac{\pi}{2}+k \pi, k \in \mathbb{Z}\right\}$ và có tập giá trị là $\mathbb{R}$

Hàm số $y=\tan x$ là hàm lẻ vì $\tan (-x)=-\tan x$

Hàm số $y=\tan x$ tuần hoàn với chu kỳ $\pi$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Các giá trị đặc biệt của hàm số $y=\tan x$

• $\tan x=0$ khi $x=k \pi$ với $k$ là một số nguyên bất kỳ
• $\tan x=1$ khi $x=\frac{\pi}{4}+k \pi$ với $k$ là một số nguyên bất kỳ
• $\tan x=-1$ khi $x=-\frac{\pi}{4}+k \pi$ với $k$ là một số nguyên bất kỳ

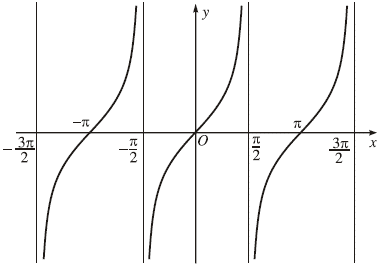
Đồ thị hàm số $y=\tan x$

#4. Hàm số lượng giác cot

Quy tắc đặt tương ứng mỗi số $x \in D=\mathbb{R}$ \ $\{k \pi \mid k \in \mathbb{Z}\}$ với số thực $\cot x=\frac{\cos x}{\sin x}$ được gọi là hàm số $\cot$

Hàm số $y=\cot x=\frac{\cos x}{\sin x}$ có tập xác định là $\mathbb{R}$ \ $\{k \pi, k \in \mathbb{Z}\}$ và có tập giá trị là $\mathbb{R}$

Hàm số $y=\cot x$ là hàm số lẻ vì $\cot (-x)=-\cot x$

Hàm số $y=\cot x$ tuần hoàn với chu kì $\pi$

Các giá trị đặc biệt của hàm số $y=\cot x$

• $\cot x=0$ khi $x=\frac{\pi}{2}+k \pi$ với $k$ là một số nguyên bất kỳ
• $\cot x=1$ khi $x=\frac{\pi}{4}+k \pi$ với $k$ là một số nguyên bất kỳ
• $\cot x=-1$ khi $x=-\frac{\pi}{4}+k \pi$ với $k$ là một số nguyên bất kỳ

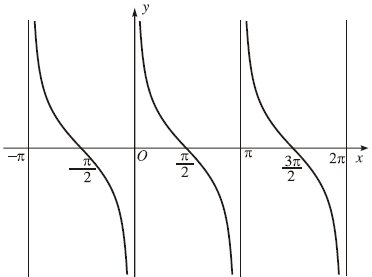
Đồ thị của hàm số $y=\cot x$

#5. Lời kết

Okay, như vậy là qua bài viết này thì bạn đã biết cách tìm tập xác định, tính chẵn lẻ, chu kỳ, cũng như đồ thị của hàm số lượng giác rồi nhé.

Các nội dung mà mình vừa trình bày ở bên trên sẽ là tiền đề quan trọng, giúp các bạn giải được các phương trình lượng giác, cũng như bất phương trình lượng giác cơ bản.

Riêng việc giải các phương trình lượng giác, bất phương trình lượng giác nâng cao thì cần kết hợp thêm các công thức lượng giác và các phương pháp giải phù hợp.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 9 công thức lượng giác cần phải nhớ !
• Cách giải phương trình lượng giác (có nhiều ví dụ)
• Hướng dẫn giải các phương trình lượng giác cơ bản

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn