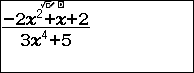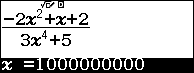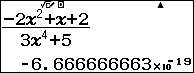Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Xin chào tất cả các bạn !
Giới hạn là một trong các nội dung cơ bản của Toán học giải tích.
Hầu hết các khái niệm của Giải tích đều được định nghĩa dựa trên giới hạn nên có thể nói không có giới hạn thì không có Giải tích.
Hôm nay, chúng ta sẽ cùng nhau tìm hiểu cách tính giới hạn của một dãy số bất bằng phương pháp Toán học và bằng máy tính cầm tay nhé các bạn (máy Casio).
Mục Lục Nội Dung
I. Giới hạn hữu hạn của dãy số
#1. Giới hạn hữu hạn của dãy số là gì?
Chúng ta nói rằng dãy số $\left(u_n\right)$ có giới hạn là $0$ khi $n$ tiến đến dương vô cực và viết $\lim _{n \rightarrow \infty} u_n=0$ hoặc $u_n \rightarrow 0$ khi $u_n \rightarrow+\infty$ nếu $|u|$ có thể nhỏ hơn một số dương bé tùy ý kể từ một số hạng nào đó trở đi.
Chúng ta nói rằng dãy số $\left(v_n\right)$ có giới hạn là số thực $a$ khi $n$ tiến đến dưong vô cực và viết $\lim _{n \rightarrow \infty} v_n=a$ hoặc $v_n \rightarrow a$ khi $n \rightarrow+\infty$ nếu $\lim _{n \rightarrow \infty}\left(v_n-a\right)=0$
#2. Một vài giới hạn đặc biệt
$\lim _{n \rightarrow+\infty} \frac{1}{n}=0$
Với $k$ là một số nguyên dương chúng ta có giới hạn $\lim _{n \rightarrow+\infty} \frac{1}{n^k}=0$
Nếu $|q|<1$ thì $\lim q^n=0$
Nếu $u_n=c$ và $c$ là hằng số thì $\lim _{n \rightarrow+\infty} u_n=\lim _{n \rightarrow+\infty} c=c$
II. Định lý về giới hạn hữu hạn
Nếu $\lim u_n=a, \lim v_n=b$ thì:
- $\lim \left(u_n+v_n\right)=a+b$
- $\lim \left(u_n-v_n\right)=a-b$
- $\lim \left(u_n v_n\right)=a \cdot b$
- Với $b$ khác $0$ chúng ta có công thức $\lim \frac{u_n}{v_n}=\frac{a}{b}$
- Nếu $u_n \geq 0$ với mọi $n$ và lim $u_n=a$ thì $a \geq 0$ và $\lim \sqrt{u_n}=\sqrt{a}$
III. Tổng của một cấp số nhân lùi vô hạn
Cấp số nhân vô hạn $u_1, u_2, u_3, \ldots, u_n, \ldots$ với công bội $q$ và $|q|<1$ được gọi là cấp số nhân lùi vô hạn.
Lúc bấy giờ tổng $S$ của cấp số nhân được tính theo công thức $S=u_1+u_1 q+u_1 q^2+\ldots=\frac{u_1}{1-q}$
IV. Giới hạn vô cực
#1. Giới hạn vô cực là gì?
Chúng ta nói dãy số $\left(u_n\right)$ có giới hạn $+\infty$ khi $n \rightarrow+\infty$ nếu $u_n$ có thể lớn hơn một số dương bất kỳ kể từ một số hạng nào đó trở đi
Lúc bấy giờ chúng ta viết lim $\left(u_n\right)=+\infty$ hoặc $u_n \rightarrow+\infty$ khi $n \rightarrow+\infty$.
Chúng ta lại nói dãy số $\left(u_n\right)$ có giới hạn $-\infty$ khi $n \rightarrow+\infty$ nếu $u_n$ có thể nhỏ hơn môt số âm bất kì kể từ một số hạng nào đó trở đi
Lúc bấy giờ chúng ta lại viết $\lim \left(u_n\right)=-\infty$ hoặc $u_n \rightarrow-\infty$ khi $n \rightarrow+\infty$
#2. Một vài giới hạn đặc biệt
Với $k$ nguyên dương chúng ta có công thức $\lim n^k=+\infty$
Nếu $q>1$ thì $\lim q^n=+\infty$.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
#3. Định lý về giới hạn vô cực
Nếu $\lim u_n=a$ và lim $v_n=\pm \infty$ thì $\lim \frac{u_n}{v_n}=0$
Nếu $\lim u_n=a>0$ và $\lim v_n=0$ và $v_n>0$ với mọi $n$ thì $\lim \frac{u_n}{v_n}=+\infty$
Nếu $\lim u_n=+\infty$ và $\lim v_n=a>0$ thì $\lim \left(u_n v_n\right)=+\infty$
V. Thủ thuật tính giới hạn của dãy số bằng máy Casio
Trên thị trường hiện tại có rất nhiều loại máy tính cầm tay khác nhau, ở đây mình sẽ hướng dẫn các bạn thực hành trên CASIO fx 580 VN X.
Bước 1. Nhập dãy số vào máy tính cầm tay.
Bước 2. Nhấn phím CALC => nhập $10^9$ => nhấn phím =
Bước 3. Nhấn phím =
Bước 4. Quan sát giá trị đang hiển thị trên màn hình máy tính cầm tay rồi suy ra giới hạn cần tìm.
| Trường hợp | Nếu giá trị đang hiển thị trên màn hình máy tính có dạng … | … thì kết quả là … |
| 1 | $-a \times 10^n$ với $a \in R^+$ và $n \in N^*$ | $-\infty$ |
| 2 | $a \times 10^{-n}$ với $a \in R$ và $n \in N^*$ | $0$ |
| 3 | $a \times 10^n$ với $a \in R^+$ và $n \in N^*$ | $+\infty$ |
| 4 | $a$ với $a \in R^*$ | $a$ |
Chẳng hạn mình cần tính giới hạn của dãy số $\frac{-2n^2+n+2}{3n^4+5}$ thì thực hiện tuần tự theo các bước bên dưới:
Bước 1. Nhập dãy số vào máy tính..
Bước 2. Nhấn phím CALC => nhập $10^9$ => nhấn phím =
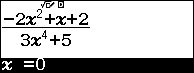
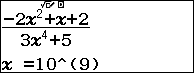
Bước 3. Nhấn phím =
Bước 4. Vì giá trị trên màn hình máy tính cầm tay rơi vào Trường hợp 2 nên giới hạn của dãy số đã cho là $0$
Vậy $\lim \frac{-2n^2+n+2}{3n^4+5}=0$
VI. Lời kết
Vâng, như vậy là qua bài viết này thì bạn đã biết cách tính giới hạn của dãy số rồi đúng không.
Nếu bạn tính giới hạn của dãy số bằng kiến thức Toán học thì không có gì để bàn, nhưng nếu bạn tính bằng máy tính cầm tay thì cần chú ý.
- Nếu dãy số có chứa các hàm số lượng giác $\sin, \cos, \tan$ thì cần cài đặt đơn vị góc là rađian
- Nếu dãy số có chứa các hàm số lượng giác $\sin, \cos, \tan$ thì $CALC~10^6$ vì $10^9$ vượt quá giá trị đầu vào của các hàm số lượng giác
- Nếu dãy số có chứ các hàm số mũ thì $CALC~10^2$ vì $10^9$ vượt quá khả năng tính toán của máy tính cầm tay
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
