3 cách chứng minh tam giác đồng dạng, có ví dụ dễ hiểu

Trong thực tế, chúng ta thường gặp rất nhiều hình có hình dạng giống nhau, nhưng kích thước khác nhau. Những cặp hình như vậy được gọi là đồng dạng (có cùng hình dạng).

Trong Toán học cũng vậy, chúng ta cũng có rất nhiều hình đồng dạng. Tuy nhiên, trong khuân khổ của bài viết này mình sẽ trình trường hợp đồng dạng của tam giác, các hình khác các bạn có thể tự tìm hiểu thêm nếu muốn nhé.

I. Hai tam giác đồng dạng là gì?

Hai tam giác được gọi là đồng dạng nếu chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.

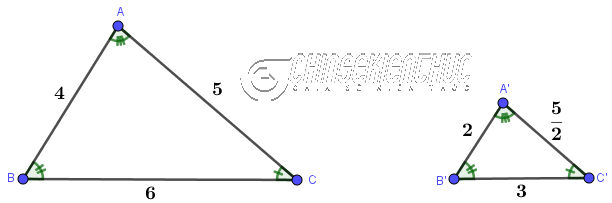
Ví dụ như ở hình bên trên: Tam giác A’B’C’ đồng dạng với tam giác ABC vì …

• $\hat{A’}=\hat{A}, \hat{B’}=\hat{B}, \hat{C’}=\hat{C}$
• $\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}$

Tam giác A’B’C’ đồng dạng với tam giác ABC được kí hiệu là $A’B’C’ ∽ ABC$

II. Các trường hợp đồng dạng của tam giác

Đọc thêm:

• MathType: Tạo ký hiệu song song, đồng dạng, cung lượng giác..
• Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

#1. Trường hợp 2 tam giác đồng dạng thứ nhất: Cạnh – Cạnh – Cạnh

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia, thì hai tam giác đã cho đồng dạng với nhau.

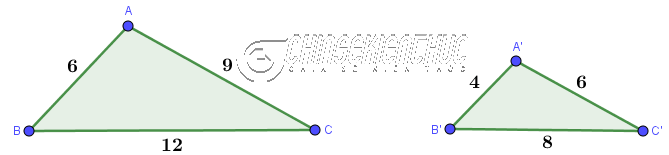
Ví dụ 1. Tam giác ABC có đồng dạng với tam giác A’B’C’ không? Vì sao? Biết AB=6, BC=12, CA=9; A’B’=4, B’C’=8, C’A’=6

Lời giải:

Tam giác ABC đồng dạng với tam giác A’B’C’ vì $\frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}=\frac{3}{2}$

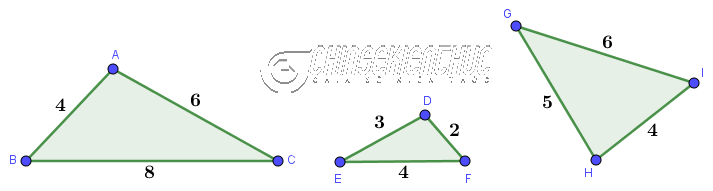
Ví dụ 2. Cặp tam giác nào trong Hình 1 đồng dạng, không đồng dạng với nhau? Vì sao?

Lời giải:

Cặp thứ nhất tam giác ABC và tam giác DFE

Tam giác ABC đồng dạng với tam giác DFE vì $\frac{AB}{DF}=\frac{BC}{FE}=\frac{CA}{ED}=\frac{1}{2}$

Chú ý: Khi ghi 2 tam giác đồng dạng với nhau ta cần ghi theo thứ tự các đỉnh tương ứng bằng nhau nha các bạn.

Cặp thứ 2, tam giác ABC và tam giác HIG

Xét tam giác ABC và tam giác HIG

• $\frac{AB}{HI}=\frac{4}{4}=1$
• $\frac{BC}{IG}=\frac{8}{6}=\frac{4}{3}$

Suy ra $\frac{AB}{HI} \neq \frac{BC}{IG}$

=> Vậy tam giác ABC không đồng dạng với tam giác HIG

Cặp thứ 3, tam giác DEF và tam giác HGI

Xét tam giác DEF và tam giác HGI

• $\frac{DE}{HG}=\frac{3}{5}$
• $\frac{EF}{GI}=\frac{4}{6}=\frac{2}{3}$

Suy ra $\frac{DE}{HG} \neq \frac{EF}{GI}$

=> Vậy tam giác DEF không đồng dạng với tam giác HGI

#2. Trường hợp 2 tam giác đồng dạng thứ 2: Cạnh – Góc – Cạnh

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi hai cặp cạnh đó (góc xen giữa cặp cạnh đó) bằng nhau => thì hai tam giác đã cho đồng dạng với nhau.

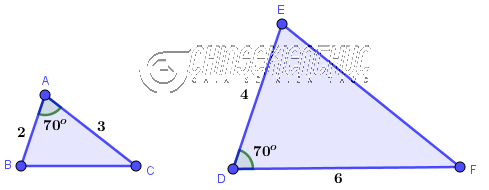
Ví dụ 3. Tam giác ABC có đồng dạng với tam giác DEF không? Vì sao? Biết AB=2, DE=4, CA=3; FD=6, $\widehat{BAC}=\widehat{EDF}=70^o$

Lời giải:

Tam giác ABC đồng dạng với tam giác DEF vì $\frac{AB}{DF}=\frac{CA}{FD}=\frac{1}{2}$ và $\widehat{BAC}=\widehat{EDF}=70^o$

#3. Trường hợp đồng dạng thứ 3: Góc – Góc

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia => thì hai tam giác đã cho đồng dạng với nhau.

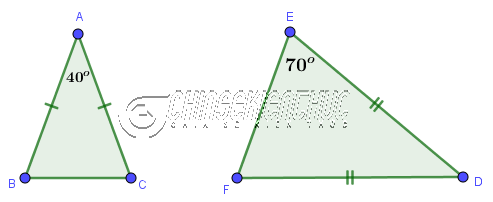
Ví dụ 4. Chứng minh tam giác ABC đồng dạng với tam giác DEF biết $AB=AC, DE=DF, \hat{A}=40^o, \hat{E}=70^o$

Lời giải:

Xét tam giác ABC

Ta có $AB=AC$ suy ra tam giác ABC cân tại A ⁽¹⁾

Mặc khác ta lại có $\hat{A}=40^o$ ⁽²⁾

Từ ⁽¹⁾ và ⁽²⁾ suy ra $\hat{B}=\hat{C}=70^o$

Xét tam giác DEF

Ta có $DE=DF$ suy ra tam giác DEF cân tại D ⁽³⁾

Mặc khác ta lại có $\hat{E}=70^o$ ⁽⁴⁾

Từ ⁽³⁾ và ⁽⁴⁾ suy ra $\hat{F}=70^o$

Suy ra $\hat{D}=40^o$

Vậy ABC đồng dạng với tam giác DEF (Góc – Góc)

III. Lời kết

Vâng, như vậy là qua bài viết này thì mình tin là bạn đã hiểu hơn về tam giác đồng dạng rồi đúng không.

Không phải ngẫu nhiên mà chúng ta cần đến ba trường hợp đồng dạng, nếu không có ba trường hợp này thì chúng ta sẽ phải chứng minh tam giác đồng dạng dựa vào định nghĩa.

Mà việc chứng minh dựa vào định nghĩa tốn khá nhiều thời gian và công sức.Hơn nữa, không phải trường hợp nào chúng ta cũng đủ giả thuyết để chứng minh.

Trong Toán học cũng như trong thực tế, không có gì là tự nhiên cả, không có gì là vô dụng cả, tất cả đều có giá trị của nó, nếu chúng ta biết vận dụng đúng cách thì sẽ tiết kiệm được rất nhiều thời gian. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com