Tập hợp các số tự nhiên là gì & Kí hiệu tập hợp các số tự nhiên

Tập hợp các số tự nhiên là một tập hợp như thế nào? Và các bước biểu diễn một số tự nhiên trên tia số ra làm sao?

Đó là hai câu hỏi cơ bản mà bạn cần trả lời được khi tìm hiểu về tập hợp các số tự nhiên.

Ngoài việc giúp bạn trả lời hai câu hỏi trên thì thông qua bài viết này, mình cũng giới thiệu thêm cách sử dụng hàm ARABIC và ROMAN của để chuyển một số Ả Rập sang số La Mã và ngược lại

#1. Tập hợp các số tự nhiên là gì?

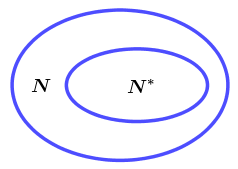
Tập hợp các số tự nhiên được kí hiệu là N (N là kí tự đầu tiên trong từ Naturel mà khi dịch sang tiếng Việt có nghĩa là tự nhiên).

Số tự nhiên là tập hợp những số lớn hơn hoặc bằng 0.

Tập hợp các số tự nhiên là một trong những tập hợp số học cơ bản nhất và thường gặp nhất.

$N=\{0; 1; 2; 3; 4; 5; …\}$

Tập hợp các số tự nhiên khác 0 được kí hiệu là $N^*$

$N^*=\{1; 2; 3; 4; 5; 6; …\}$

Chú ý: $N^* \subset N$

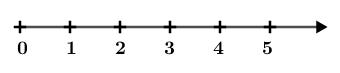
#2. Các bước biểu diễn số tự nhiên trên tia số

Bước 1. Dùng thước thẳng, bắt đầu từ điểm 0 vạch thẳng từ trái sang phải.

Bước 2. Lấy một đoạn thẳng làm đơn vị đo (1cm, 1inch, …).

Bước 3. Bắt đầu từ 0 đặt liên tiếp các đoạn thẳng đơn vị, ta sẽ hoàn thành một tia số.

Khi muốn biểu diễn số tự nhiên a ta lấy trên tia số điểm cách 0 một khoảng cách a đơn vị đã chọn.

#3. Thứ tự trong tập hợp các số tự nhiên

Cho hai số tự nhiên khác nhau bao giờ cũng có một số nhỏ và một số lớn. Khi biểu diễn hai số này trên tia số thì điểm biểu diễn số nhỏ nằm bên trái điểm biểu diễn số lớn.

Số a nhỏ hơn số b kí hiệu $a<b$, lúc bấy giờ ta cũng có thể nói b lớn hơn a, kí hiệu $b >a$

Quan hệ thứ tự của các số tự nhiên có tính chất bắc cầu

$\left.\begin{array}{ll}a < b \\ b < c \end{array}\right \} \Rightarrow a < c$ hoặc $\left.\begin{array}{ll}a > b \\ b > c \end{array}\right \} \Rightarrow a > c$

Chú ý:

• Kí hiệu $a \geq b$ để chỉ a lớn hơn hoặc bằng b, $a \leq b$ để chỉ a nhỏ hơn hoặc bằng b
• Số tự nhiên nhỏ nhất là số 0 và không có số tự nhiên lớn nhất.
• Số tự nhiên khác 0 nhỏ nhất là số 1 và không có số tự nhiên lớn nhất.
• Nếu giữa hai số tự nhiên a và b không có số tự nhiên nào khác và $a< b$ thì a gọi là số liên trước của b và ngược lại b là số liền sau của a.

#4. Ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân người ta dùng tất cả mười chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 và giá trị của mỗi chữ số trong một số phụ thuộc vào vị trí của nó “mười đơn vị ở một hàng làm thành một đơn vị ở hàng liền trước”

Cho số 2022 ta có $2 \times 1000+0 \times 100 + 2 \times 10+ 2$. Chữ số 2 đầu tiên có giá trị gấp một nghìn lần chữ số 2 cuối cùng và gấp một trăm lần chữ số 2 áp cuối.

Trường hợp cần ghi một số tự nhiên không cụ thể, chẳng hạn số tự nhiên có ba chữ số thì ta sẽ ghi $\overline{abc}$. Các kí tự a, b, c là đại diện cho một chữ số nào đó trong mười chữ số 0, 1, 2, …, 9 và số đầu tiên $a \neq 0$

Chú ý: Chúng ta không được bỏ dấu gạch ngang, vì khi đó abc sẽ được hiểu là $a \times b \times c$

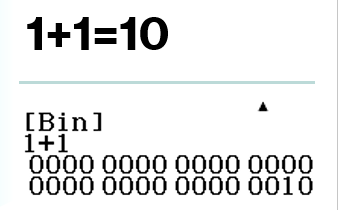
Những điều vừa trình bày ở đây chỉ đúng trong hệ thập phân, còn trong các hệ số khác như hệ nhị phân, lục phân, bát phân, thập nhị phân, thập lục thập, …, thì không còn đúng nữa.

Đây là lý do tại sao $1 + 1 = 10$ (trong hệ nhị phân), một chục dừa lại có 12 trái (trong hệ thập nhị phân).

Ngoài ra, khi cần tính toán với các hệ số khác hệ thập phân, bạn có sử dụng phương thức tính toán Base – N của máy tính CASIO fx-580VN X

#5. Cách chuyển một số Ả Rập sang số La Mã và ngược lại

Ngày nay số La Mã tuy không còn được sử dụng phổ biến nhưng trong một số trường hợp đặc thù thì nó vẫn còn.

Chẳng hạn số trên mặt đồng hồ, trình bày bảng khi giảng dạy, trình bày mục lục trong sách, …

Để viết số La Mã chúng ta cần sử dụng bảy chữ số mà kí hiệu và giá trị tương ứng trong của chúng hệ thập phân là:

Kí hiệu chữ số La Mã	I	V	X	L	C	D	M
Giá trị tương ứng trong hệ thập phân	1	5	10	50	100	500	1000

Các chữ số của số La Mã không thay đổi theo vị trí, các chữ số có giá trị lớn ghi trước các chữ số có giá trị nhỏ.

Trong một số La Mã các chữ số V, L, D không ghi quá một lần; các chữ số M, C, X, I không ghi quá ba lần.

Giá trị của một số bằng tổng các thành phần của nó.

Chuyển số La Mã MMXXII sang số Ả Rập

Trước hết ta nhận xét rằng số MMXXII không có sáu số đặc biệt nên ta có thể viết số này thành tổng các thành phần của nó

$MMXXII$

$=MM+XX+II$

$=2000+20+2$

$=2022$

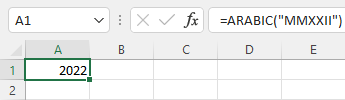
Nếu sử dụng Excel thì bạn có thể sử dụng hàm =ARABIC(text) để chuyển một số La Mã sang số Ả Rập

Chú ý: Số lớn nhất mà hàm ARABIC có thể chuyển được là 255.000

Ví dụ. Chuyển số Ả Rập 2022 sang số La Mã

Ta phân tích số 2022 thành tổng các thành phần tương ứng với các số La Mã

$2022$

$=2000+20+2$

$=MM+XX+II$

$=MMXXII$

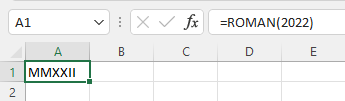
Hàm =ROMAN(number, [form]) của Excel cho phép chúng ta chuyển một số La Mã sang số Ả rập

Chú ý: Số lớn nhất mà hàm ROMAN có thể chuyển được là 3 999

#6. Lời kết

Thay cho một lời kết ở đây mình xin gửi đến các bạn một lưu ý (rất nhiều bạn nhằm lẫn cho này).

Mỗi số tự nhiên đều biểu diễn được bởi một điểm trên tia số nhưng điều ngược lại không đúng, không phải mỗi điểm trên tia số đều biểu diễn một số tự nhiên.

Okay, hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com