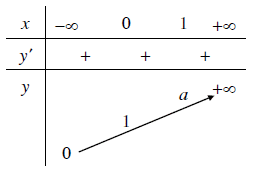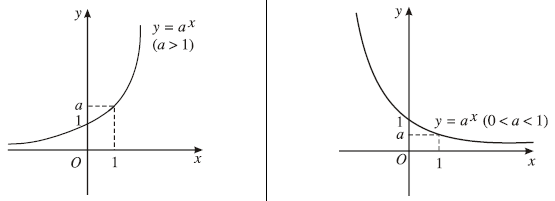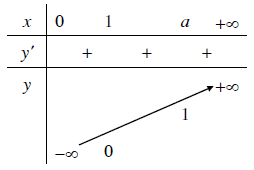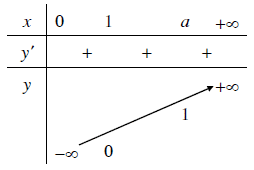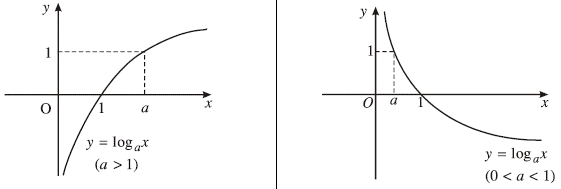Tìm tập xác định, đạo hàm, đồ thị.. của hàm số (lũy thừa, mũ và lôgarit)

Xin chào tất cả các bạn !

Hôm nay, chúng ta sẽ cùng nhau tìm hiểu về tập xác định, đạo hàm, tính đơn điệu (đồng biến, nghịch biến), đồ thị của hàm số lũy thừa, hàm số mũ, hàm số lôgarit.

Việc tìm hiểu này có nhiều hữu ích trong quá trình học tập, kiểm tra và thi cử.

Dễ thấy nhất là khi giải phương trình, bất phương trình mũ, cũng như phương trình và bất phương trình lôgarit.

#1. Tập xác định, đạo hàm, tính đơn điệu, đồ thị của hàm số lũy thừa

Xét hàm số lũy thừa $y=x^\alpha$ với $\alpha$ là một số thực bất kỳ.

Lúc này chúng ta có:

1.1. Tập xác định

Tập xác định $D$ của hàm số lũy thừa $y=x^\alpha$ phụ thuộc vào giá trị của $\alpha$

• Nếu $\alpha$ là một số nguyên dương thì $D=R$
• Nếu $\alpha$ là một số nguyên âm hoặc số $0$ thì $D=R$ \ $0$
• Nếu $\alpha$ không là số nguyên thì $D=(0, +\infty)$

1.2. Đạo hàm

$y’=(x^\alpha)’=\alpha x^{\alpha-1}$ với mọi $x$ dương.

1.3. Tính đơn điệu

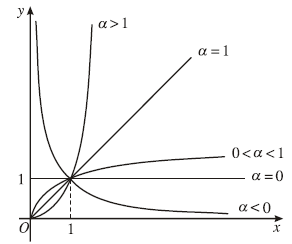
Tính đơn điệu của hàm số lũy thừa trên khoảng $(0, +\infty)$ phụ thuộc vào dấu của $\alpha$

Nếu $\alpha>0$ thì $y$ đồng biến trên $(0, +\infty)$

Nếu $\alpha<0$ thì $y$ nghịch biến trên $(0, +\infty)$

Nếu $n$ là số nguyên dương, $a$ là số dương, $b$ là số dương thì chúng ta còn có:

• $a>b \Leftrightarrow a^n > b^n$
• $a>b \Leftrightarrow \sqrt[n]{a} > \sqrt[n]{b}$

1.4. Đồ thị

Đồ thị của hàm số lũy thừa:

• Luôn đi qua điểm có tọa độ $(1, 1)$
• Nếu $\alpha$ dương thì độ thị không có đường tiệm cận
• Nếu $\alpha$ âm thì đồ thị nhận trục hoành làm đường tiệm cận ngang, nhận trục tung làm đường tiệm cận đứng.

#2. Tập xác định, đạo hàm, tính đơn điệu, đồ thị của hàm số mũ

Xét hàm số mũ $y=a^x$ với $a$ là một số thực dương khác $1$

Lúc này ta có:

2.1. Tập xác định

Mọi hàm số mũ đều có tập xác định là $D=R$

2.2. Đạo hàm

$y’=(a^x)’=a^x \ln a$

Đặc biệt $(e^x)’=e^x$

2.3. Tính đơn điệu

Tính đơn điệu của hàm số mũ phụ thuộc vào dấu của $a$

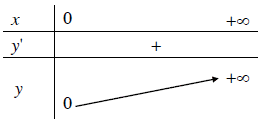
Nếu $a>1$ thì hàm số đồng biến trên $R$

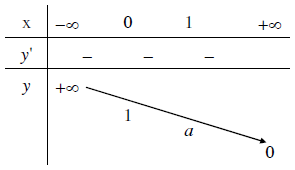
Nếu $0<a<1$ thì hàm số nghịch biến trên $R$

2.4. Đồ thị

Đồ thị của hàm số mũ:

• Luôn cắt trục tung tại điểm có tọa độ $(0, 1)$
• Luôn nằm phía trên trục hoành
• Nhận trục hoành làm đường tiệm cận ngang.

#3. Tập xác định, đạo hàm, đơn điệu, đồ thị của hàm số lôgarit

Xét hàm số lôgarit $y=\log_a x$ với $a$ là một số thực dương khác $1$

Lúc này ta có:

3.1. Tập xác định

Mọi hàm số lôgarit đều có tập xác định $D=(0, +\infty)$

3.2. Đạo hàm

$y’=(\log_a x)’=\frac{1}{x \ln a}$

Đặc biệt $(\ln x)’=\frac{1}{x}$

3.3. Tính đơn điệu

Tương tự như hàm số mũ, tính đơn điệu của hàm số lôgarit phụ thuộc vào giá trị của $a$

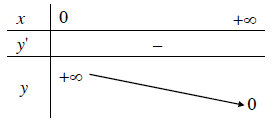
Nếu $a>1$ thì hàm số đồng biến trên $R$

Nếu $0<a<1$ thì hàm số nghịch biến trên $R$

3.4. Đồ thị

Đồ thị của hàm số mũ:

• Luôn cắt trục hoành tại điểm có tọa độ $(1, 0)$
• Luôn nằm phía bên phải của trục tung
• Nhận trục tung làm đường tiệm cận đứng

#4. Lời kết

Hàm số lũy thừa, hàm số mũ và hàm số lôgarit là một trong những hàm số cuối cùng được giới thiệu chương trình Toán học Trung học.

Nếu bạn không theo học chuyên ngành sư phạm Toán học hoặc các ngành có liên quan thì gần như bạn sẽ không bao giờ có nhu cầu tiếp cận các hàm số khác.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn