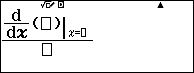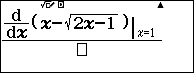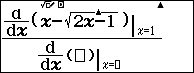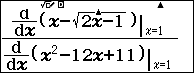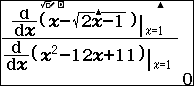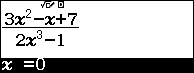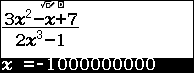Cách tính giới hạn của hàm số bằng máy tính Casio

Xin chào tất cả các bạn !

Việc tính giới hạn của hàm số tương tự như việc tính giới hạn của dãy số nhưng có phần phức tạp hơn một chút.

Nguyên nhân là ngoài giới hạn tại vô cực thì hàm số còn có tại một điểm và giới hạn một bên.

#1. Định lý về giới hạn hữu hạn

Các định lí về giới hạn hữu hạn của hàm số được suy ra từ các định lí về giới hạn của dãy số.

Giả sử $\lim _{x \rightarrow x_0} f(x)=L$ và $\lim _{x \rightarrow x_0} g(x)=M$

Lúc này chúng ta có …

• $\lim _{x \rightarrow x_0}[f(x)+g(x)]=L+M$
• $\lim _{x \rightarrow x_0}[f(x)-g(x)]=L-M$
• $\lim _{x \rightarrow x_0}[f(x) \cdot g(x)]=L \cdot M$
• Với $M$ khác $0$ chúng ta còn có $\lim _{x \rightarrow x_0} \frac{f(x)}{g(x)}=\frac{L}{M}$

Nếu $f(x) \geq 0$ với mọi $x \in J$ \ $\left\{x_0\right\}$ và $J$ là một khoảng nào đó chứa $x_{0}$ thì $L \geq 0$ và $\lim _{x \rightarrow x_0} \sqrt{f(x)}=\sqrt{L}$

Các nội dung vừa trình bày vẫn đúng khi thay $x \rightarrow x_0$ bởi $x \rightarrow+\infty$ hoặc $x \rightarrow-\infty$

#2. Một vài giới hạn hàm số đáng nhớ

Áp dụng định nghĩa giới hạn của hàm số chúng ta có thể suy ra được các giới hạn đặc biệt như:

• Với $k$ là một số nguyên dương chúng ta có $\lim _{x \rightarrow+\infty} x^k=+\infty$
• Nếu $k$ là số lẻ thì $\lim _{x \rightarrow-\infty} x^k=-\infty$
• Nếu $k$ là số chẵn thì $\lim _{x \rightarrow-\infty} x^k=+\infty$

#3. Một vài quy tắc về giới hạn vô cực của hàm số

Dưới đây là một số quy tắc tính giới hạn tích và thương của hai hàm số khi một trong hai hàm số có giới hạn vô cực.

Nếu $\lim _{x \rightarrow x_0} f(x)=L \neq 0$ và $\lim _{x \rightarrow x_0} g(x)=\pm \infty$ thì:

• $\lim _{x \rightarrow x_0}[f(x) \cdot g(x)]$ bằng $+\infty$ hoặc $-\infty$
• $\lim _{x \rightarrow x_0} \frac{f(x)}{g(x)}=0$
• $\lim _{x \rightarrow x_0} \frac{g(x)}{f(x)}$ bằng $+\infty$ hoặc $-\infty$

Các quy tắc vừa trình được bày vẫn đượccó thể  áp dụng cho các trường hợp $x \rightarrow x_0^{+}, x \rightarrow x_0^{-}, x \rightarrow+\infty$ và $x \rightarrow-\infty$

#4. Một số giới hạn hàm số đặc biệt

Dưới đây là một số giới hạn đặc biệt:

• $\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}=e$
• $\lim _{x \rightarrow 0} \frac{\sin x}{x}=1$
• $\lim _{x \rightarrow 0} \frac{e^x-1}{x}=1$
• $\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}=1$

#5. Quy tắc Lô-pi-tan (l’Hôpital)

Quy tắc Lô pi tan sẽ giúp chúng ta khử dạng vô định $\frac{0}{0}$ một cách chính xác và nhanh chóng.

$\left.\begin{array}{l} \lim _{x \rightarrow a} f(x)=0 \\ \lim _{x \rightarrow a} g(x)=0 \end{array}\right\} \Rightarrow \lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}$

Cách áp dụng Lô-pi-tan trên máy tính cầm tay CASIO

Chẳng hạn mình cần tìm $\lim _{x \rightarrow 1} \frac{x-\sqrt{2 x-1}}{x^2-12 x+11}$ thì thực hiện tuần tự theo các bước bên dưới:

Dễ thấy giới hạn cần tìm có dạng $\frac{0}{0}$

Bước 1. Nhấn phím

Bước 2. Nhấn phím  => nhập $x-\sqrt{2 x-1}$ => nhấn  => nhập $1$

Bước 3. Nhấn phím  => nhập $x^2-12 x+11$ => nhấn => nhập $1$

Bước 4. Nhấn phím =

Vậy $\lim _{x \rightarrow 1} \frac{x-\sqrt{2 x-1}}{x^2-12 x+11}=0$

#6. Thủ thuật tính giới hạn của hàm số bằng máy tính Casio

Ở đây mình sẽ hướng dẫn các bạn thực hành trên CASIO FX 580 VN X, với các dòng máy tính cầm tay khác các bạn thực hiện tương tự ha.

Bước 1. Nhập hàm số vào máy tính cầm tay.

Bước 2. Nhấn phím CALC => nhập giá trị => nhấn phím =

Giá trị cụ thể là bao nhiêu tùy thuộc vào giới hạn tiến đến đâu …

Nếu giới hạn tiến đến …	… thì giá trị cần nhập là …
$-\infty$	$-10^9$
$a^{-}$	$a-10^{-9}$
$a$	$a+10^{-9}$ hoặc $a-10^{-9}$
$a^{+}$	$a+10^{-9}$
$+\infty$	$10^9$

Bước 3. Nhấn phím =

Bước 4. Sau đó quan sát giá trị đang hiển thị trên màn hình máy tính cầm tay rồi suy ra giới hạn cần tìm.

Trường hợp	Nếu giá trị đang hiển thị trên màn hình máy tính có dạng …	… thì kết quả là …
1	$-a \times 10^n$ với $a \in R^+$ và $n \in N^*$	$-\infty$
2	$a \times 10^{-n}$ với $a \in R$ và $n \in N^*$	$0$
3	$a \times 10^n$ với $a \in R^+$ và $n \in N^*$	$+\infty$
4	$a$ với $a \in R^*$	$a$

Ví dụ.

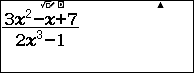
Chẳng hạn mình cần tính giới hạn của hàm số $\frac{3x^2-x+7}{2x^3-1}$ khi $x$ tiến đến $-\infty$ thì thực hiện tuần tự theo các bước bên dưới

Bước 1. Nhập hàm số vào máy tính cầm tay.

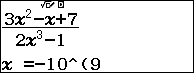
Bước 2. Nhấn phím CALC => vì $x$ tiến đến $-\infty$ nên chúng ta sẽ nhập $-10^9$ => nhấn phím =

Bước 3. Nhấn phím =

Bước 4. Vì giá trị trên màn hình máy tính cầm tay rơi vào Trường hợp 2 nên giới hạn của hàm số đã cho là $0$

Vậy $\lim_{x \rightarrow -\infty}\frac{3x^2-x+7}{2x^3-1}=0$

#7. Lời kết

Vâng, như vậy là qua bài viết này thì bạn đã biết cách tính giới hạn của hàm số bằng máy tính Casio rồi đúng không.

Nếu bạn tính giới hạn của hàm số bằng kiến thức Toán học thì không có gì để bàn, nhưng nếu bạn tính bằng máy tính cầm tay thì cần chú ý như sau:

• Nếu hàm số có chứa các hàm số lượng giác $\sin, \cos, \tan$ thì cần cài đặt đơn vị góc là rađian 

Nhấn lần lượt các phím 

• Khi giá trị xuất hiện trên màn hình máy tính cầm tay là một số vô tỉ thì cần phải xử lí cẩn thận.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tìm tập xác định của hàm số (có mẹo hay)
• 10 công thức tính vi phân của các hàm số thường gặp
• Công thức tính nguyên hàm của các hàm số thường gặp
• Cách vẽ đồ thị hàm số bậc nhất (trên giấy & trên máy tính)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn