Cách tìm nhanh phương trình đặc trưng của ma trận cấp ba

Trong bài viết cách tính định thức của ma trận cấp ba mình đã kết luận ma trận vuông cấp 3 x 3 là ma trận vuông thường gặp nhất.

Vậy nên không có gì khó hiểu khi phương trình đặc trưng của ma trận vuông cấp 3 x 3 cũng là phương trình thường gặp nhất.

Hôm nay, mình sẽ hướng dẫn cho các bạn ba cách tím nhanh phương trình đặc trưng của ma trận vuông cấp 3 x 3.

Trong ba cách này thì cách thứ 2 là đặc biệt nhất và cũng là cách tím nhanh nhất (trừ cách tính bằng công cụ trực tuyến Wolfram Alpha ra 😀 )

I. Phương trình đặc trưng là gì?

Phương trình có dạng $det(A-\lambda I)=0$ với A là ma trận vuông cấp n x n, I là ma trận đơn vị cấp n x n được gọi là phương trình đặc trưng của ma trận A.

Nếu ma trận A là $\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right)$ thì phương trình đặc trưng sẽ là:

$\left|\begin{array}{ccc} a_{11}-\lambda & a_{12} & a_{13} \\ a_{21} & a_{22}-\lambda & a_{23} \\ a_{31} & a_{32} & a_{33}-\lambda \end{array}\right|=0$

Ví dụ. Tìm phương trình đặc trưng của ma trận $A=\left(\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right)$

Lời giải:

Ta có $A-\lambda I=\left(\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right)-\lambda\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)=\left(\begin{array}{ccc} 5-\lambda & 4 & 7 \\ 5 & 7-\lambda & 8 \\ 9 & 6 & 9-\lambda \end{array}\right)$

Suy ra phương trình đặc trưng của ma trận A là $det(A-\lambda I)=0~(*)$

$(*) \Leftrightarrow \left|\begin{array}{ccc} 5-\lambda & 4 & 7 \\ 5 & 7-\lambda & 8 \\ 9 & 6 & 9-\lambda \end{array}\right|=0$

Việc biểu diễn phương trình này thành dạng đại số sơ cấp xem chi tiết ở mỗi cách bên dưới:

Cách #1. Dựa vào định thức của ma trận vuông cấp 3 x 3

Ở đây chúng ta sẽ xem đa thức đặc trưng như một định thức của ma trận vuông cấp 3 x 3. Từ đó việc tính định thức sẽ tương đương việc biến đổi đa thức đặc trưng từ dạng đại số cao cấp sang dạng đại số sơ cấp.

Chúng ta biến đổi đa thức đặc trưng sang dạng đại số sơ cấp là để tìm được các giá trị riêng từ đó phục vụ việc tìm véc tơ riêng, chéo hóa ma trận, …

Lời giải:

$(*) \Leftrightarrow \left|\begin{array}{ccc} 5-\lambda & 4 & 7 \\ 5 & 7-\lambda & 8 \\ 9 & 6 & 9-\lambda \end{array}\right|=0$

$(*) \Leftrightarrow (5-\lambda)\left|\begin{array}{cc} 7-\lambda & 8 \\ 6 & 9-\lambda \end{array}\right|-4\left|\begin{array}{cc} 5 & 8 \\ 9 & 9-\lambda \end{array}\right|+7\left|\begin{array}{cc} 5 & 7-\lambda \\ 9 & 6 \end{array}\right|=0$

$(*) \Leftrightarrow (5-\lambda)[(7-\lambda)(9-\lambda)-6.8]-4[5(9-\lambda)-9.8]+7[5.6-9(7-\lambda)]=0$

$(*) \Leftrightarrow -48-12\lambda+21\lambda^2-\lambda^3=0$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Vậy phương trình đặc trưng của ma trận A là $-48-12\lambda+21\lambda^2-\lambda^3=0$

Cách #2. Dựa vào phương trình tương đương

Phương trình tương đương này được mình tham khảo trong đề tài nghiên cứu khoa học của ThS. Trần Lê Nam

$(*) \Leftrightarrow \left|\begin{array}{ccc} a_{11}-\lambda & a_{12} & a_{13} \\ a_{21} & a_{22}-\lambda & a_{23} \\ a_{31} & a_{32} & a_{33}-\lambda \end{array}\right|=0$

$(*) \Leftrightarrow -\lambda^3+(a_{11}+a_{22}+a_{33})\lambda^2-\left(\left|\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right| +\left|\begin{array}{cc} a_{11} & a_{13} \\ a_{31} & a_{33} \end{array}\right|+\left|\begin{array}{cc} a_{22} & a_{23} \\ a_{32} & a_{33} \end{array}\right|\right)\lambda+\left|\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right|=0$

Lúc bấy giờ, việc biến đổi phương trình đặc trưng của ma trận A từ dạng đại số cao cấp sang dạng đại số sơ cấp đã nhanh hơn khá nhiều.

Lời giải:

$(*) \Leftrightarrow \left|\begin{array}{ccc} 5-\lambda & 4 & 7 \\ 5 & 7-\lambda & 8 \\ 9 & 6 & 9-\lambda \end{array}\right|=0$

$(*) \Leftrightarrow -\lambda^3+(5+7+9)\lambda^2-\left(\left|\begin{array}{cc} 5 & 4 \\ 5 & 7 \end{array}\right| +\left|\begin{array}{cc} 5 & 7 \\ 9 & 9 \end{array}\right|+\left|\begin{array}{cc} 7 & 8 \\ 6 & 9 \end{array}\right|\right)\lambda+\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|=0$

$(*) \Leftrightarrow -\lambda^3+21\lambda^2-(15 +(-18)+15)\lambda-48=0$

$(*) \Leftrightarrow -\lambda^3+21\lambda^2-12\lambda-48=0$

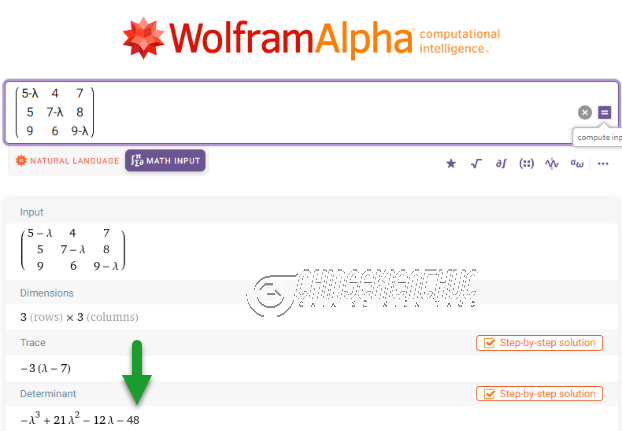
Cách #3. Sử dụng công cụ trực tuyến Wolfram Alpha

Khi sử dụng công cụ trực tuyến Wolfram Alpha hỗ trợ tìm dạng đại số sơ cấp của phương trình đặc trưng chúng ta chỉ nhập đa thức đặc trưng. Nếu nhập cả phương trình đặc trưng sẽ không thu được kết quả mong muốn.

Cách nhập đa thức đặc trưng tương tự như cách nhập ma trận, xem chi tiết cách nhập tại đây (Cách 1 của Phương pháp 3 trong bài viết này).

Đa thức tại phần Determinant chính là dạng đại số sơ cấp của đa thức đặc trưng vừa nhập.

II. Lời kết

Phương trình đặc trưng của ma trận cấp ba là một đối tượng trong Toán học cao cấp, nói cách khác là chỉ sinh viên mới gặp phương trình này.

Mặc khác đề kiểm tra, đề thi của sinh viên gần như luôn là tự luận.

Vậy nên:

• Các bạn nên ưu tiên sử dụng Cách 2 khi cần tính biến đổi phương trình đặc trưng từ dạng đại số cao cấp sang dạy đại số sơ cấp
• Cách 3 chỉ sử dụng để kiểm tra kết quả.
• Cách 1 chỉ sử dụng khi cần tìm phương trình đặc trưng của ma trận cấp 2 x 2, 4 x 4, … (thực hiện theo cấp của ma trận hiện hành).

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hạn gặp lại trong bài viết tiếp theo nhé !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn