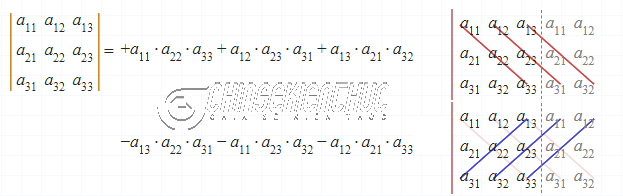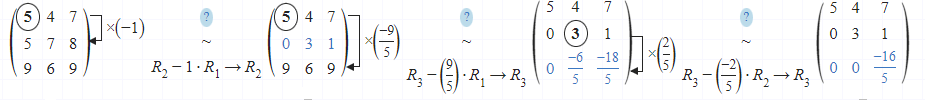Ma trận là đối tượng cơ bản của Đại số cao cấp, ma trận có rất nhiều ứng dụng trong Toán học cũng như trong các ngành khoa học khác.
Bàn về ma trận thì có rất nhiều chủ đề, nhiều phép tính. Ví dụ như phép tính cộng, phép tính nhân, tính định thức, tìm ma trận nghịch đảo, tìm hạng, …
Và trong bài viết ngày hôm nay mình sẽ hướng dẫn cho các bạn cách tính định thức của ma trận cấp ba.
Tại sao lại là tính định thức? Tại sao lại là ma trận cấp ba?
Vâng, tại vì thao tác tính định thức là thao tác thường gặp nhất khi làm việc với ma trận, còn ma trận cấp ba (ma trận vuông cấp 3 x 3) cũng là ma trận vuông thường gặp nhất trong các ma trận vuông
Mục Lục Nội Dung
I. Ma trận là gì?
Trong toán học thì Ma trận là bảng sắp xếp số liệu (gọi là phần từ của ma trận) thành hàng và cột.
Ma trận có thể có một hoặc nhiều chiều, được biểu thị bằng số hàng và số cột.
Khi định nghĩa một ma trận ta cần chỉ rõ số hàng và số cột cùng trường số của các phần tử có nó.
Ma trận $\left(\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right)$ còn được kí hiệu là $\left[\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right]$
Định thức của ma trận được ký hiệu là $\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|$
Ma trận trong tiếng Anh là Matrix, định thức là Determinant và thường được viết tắt là det
Phương pháp #1: Phương pháp Toán học
Dưới đây là ba cách tính định thức của ma trận vuông cấp 3 x 3 thường được sử dụng nhất.
Cách 1. Quy tắc tam giác
Quy tắc Tam giác về bản chất tương tự như Quy tắc của Sarrus.
$\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|=5.7.9+4.8.9+7.5.6-9.7.7-6.8.5-9.5.4=-48$
Nhận xét:
Cách này chỉ có thể tính được định thức của ma trận vuông cấp 3 x 3
Cách 2. Quy tắc của Sarrus
Mẹo nhớ của quy tắc của Sarrus là viết thêm cột 1, cột 2 vào phía bên phải của ma trận.
Sau đó tính tổng của các tích với chú ý là tích của “dấu huyền” là cộng và của “dấu sắc” là trừ.
$\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|=5.7.9+4.8.9+7.5.6-9.7.7-6.8.5-9.5.4=-48$
Nhận xét:
Cách này chỉ có thể tính được định thức của ma trận vuông cấp 3 x 3
Cách 3. Phép khử Gaussian
Phép khử Gaussian sẽ giúp chúng ta biến đổi ma trận ban đầu thành ma trận dạng tam giác. Lúc bấy giờ, tích của đường chéo chính chính là định thức của ma trận.
$\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|=\left|\begin{array}{ccc} 5 & 4 & 7 \\ 0 & 3 & 1 \\ 0 & 0 & -\frac{16}{5} \end{array}\right|=5.3.\left(-\frac{16}{5}\right)=-48$
Nhận xét:
- Phép khử Gaussian có thể tính được định thức của ma trận vuông cấp bất kì và cũng là cách được sử dụng nhiều nhất.
- Phép khử Gaussian còn được sử dụng để tìm hạng của ma trận, ma trận nghịch đảo, …
Cách 4. Khai triển định thức theo dòng hoặc cột
Ở đây mình sẽ khai triển theo dòng thứ nhất, bạn hoàn toàn có thể áp dụng cho các dòng khác hoặc cột khác.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
$\left|\begin{array}{ccc} 5 & 4 & 7 \\ 5 & 7 & 8 \\ 9 & 6 & 9 \end{array}\right|=5\left|\begin{array}{cc} 7 & 8 \\ 6 & 9 \end{array}\right|-4\left|\begin{array}{cc} 5 & 8 \\ 9 & 9 \end{array}\right|+7\left|\begin{array}{cc} 5 & 7 \\ 9 & 6 \end{array}\right|=5(7.9-6.8)-4(5.9-9.8)+7(5.6-9.7)=-48$
Nhận xét:
- Cách này có thể tính được định thức của ma trận vuông cấp bất kì, tuy nhiên chúng ta chỉ nên áp dụng đến cấp cao nhất là 5 x 5, cao hơn thì không nên áp dụng.
- Đối với cấp 5 x 5 chúng ta sẽ quy về việc tính 5 ma trận cấp 4 x 4 và chúng ta sẽ tính 5 ma trận cấp 4 x 4 bằng máy tính CASIO.
Phương pháp #2: Máy tính CASIO fx-580VN X
Bước 1. Chọn phương thức tính toán Matrix (nhấn phím MENU rồi nhấn phím 4).
Bước 2. Gán ma trận cần tính vào biến ma trận MatA (nhấn phím 1).
Bước 3. Khai báo số dòng (nhấn phím 3)
Bước 4. Khai báo số cột (nhấn phím 3)
Bước 5. Sau đó bạn lần lượt nhập các hệ số của ma trận.
Bước 6. Lần lượt nhấn các phím
Nhận xét:
Máy tính CASIO fx-580VN X có thể tính được định thức của ma trận vuông với cấp lớn nhất là 4 x 4.
Ngoài ra máy tính còn có một số tính năng như cộng, nhân, bình phương, lập phương, ma trận nghịch đảo, ma trận chuyển vị và ma trận đơn vị.
Phương pháp #3: Sử dụng ứng dụng, phần mềm
Ngoài công cụ trực tuyến WolframAlpha và phần mềm Maple ra thì bạn có thể nghiên cứu thêm ứng dụng Photomath trên điện thoại smartphone hoặc trên máy tính bảng.
Cách 1. Dịch vụ trực tuyến WolframAlpha
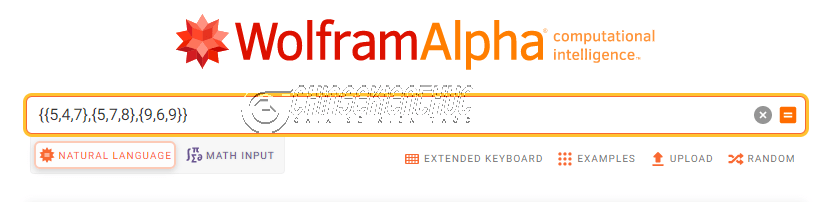
Bước 1. Bạn truy cập vào địa chỉ https://www.wolframalpha.com/
Bước 2. Nhập ma trận vào dịch vụ theo ngôn ngữ riêng của WolframAlpha là {{5,4,7},{5,7,8},{9,6,9}}
Chú ý:
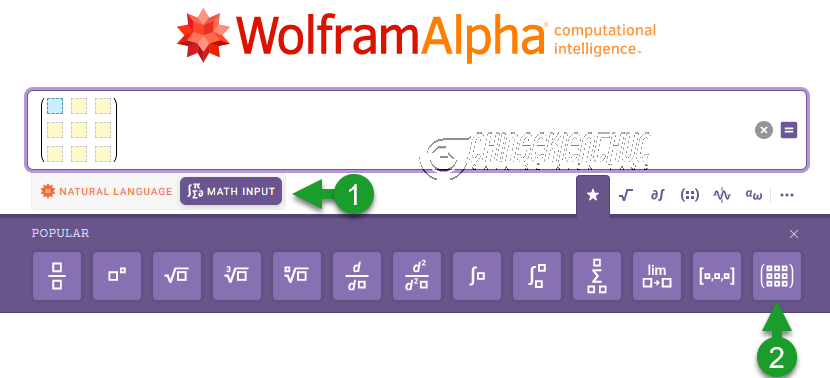
Bạn có thể nhập ma trận vào công cụ WolframAlpha theo ngôn ngữ Toán học bằng cách chọn vào MATH INPUT rồi chọn vào icon
Bước 3. Nhấn phím Enter
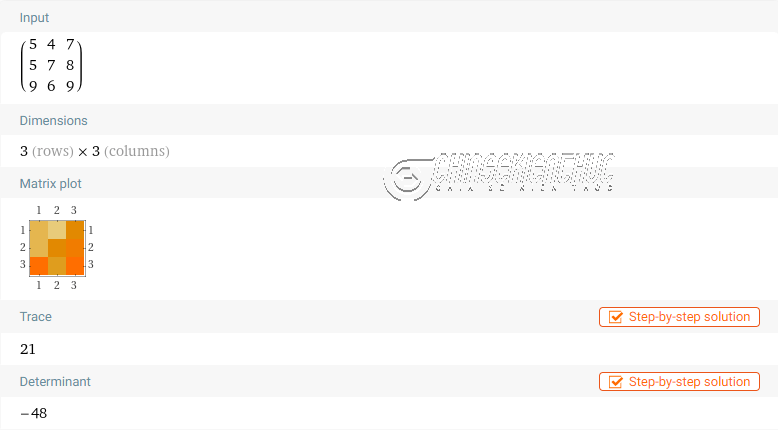
Giá trị tại dòng Determinant chính là định thức của ma trận vừa nhập.
Nhận xét:
Công cụ trực tuyến WolframAlpha có thể tính được định thức của ma trận vuông cấp bất kỳ và rất nhiều ứng dụng khác với nhiều ngành khoa học khác nhau.
Cách 2. Phần mềm Maple
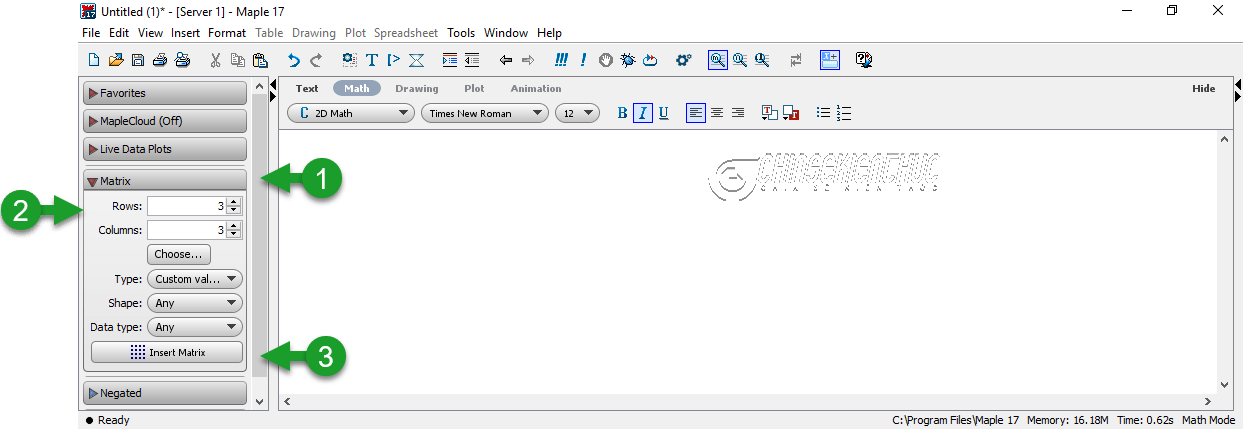
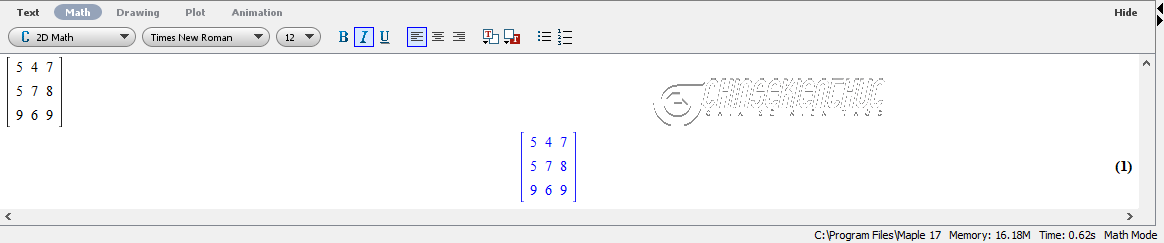
Bước 1. Khởi động phần mềm Maple lên => chọn Matrix => lần lượt nhập số dòng / số cột tại Rows / Columns => chọn Insert Matrix
Bước 2. Lần lượt nhập các hệ số của ma trận => nhấn phím Enter
Chú ý:
Bạn có thể nhập trực tiếp ma trận vào Maple theo ngôn ngữ riêng của phần mềm là matrix([[5,4,7],[5,7,8],[9,6,9]])
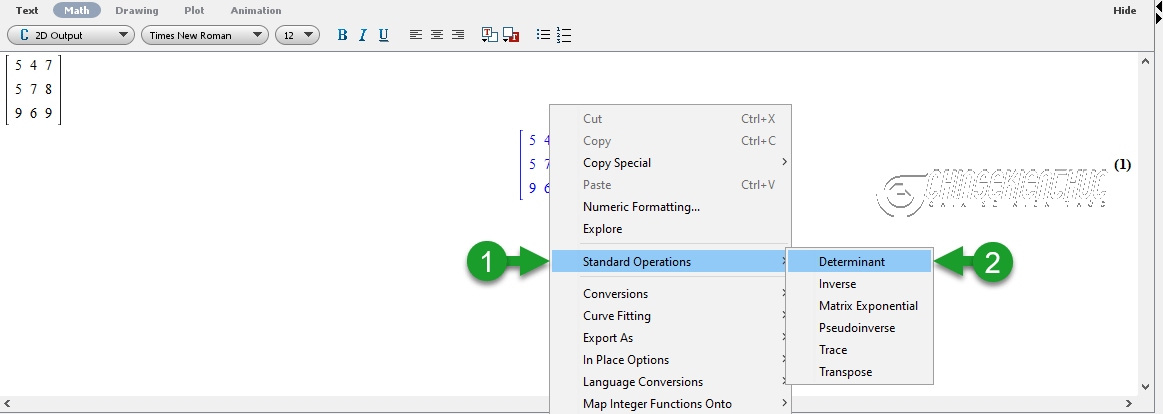
Bước 3. Nháy chuột phải vào ma trận => rồi chọn Standard Operations => chọn Determinant
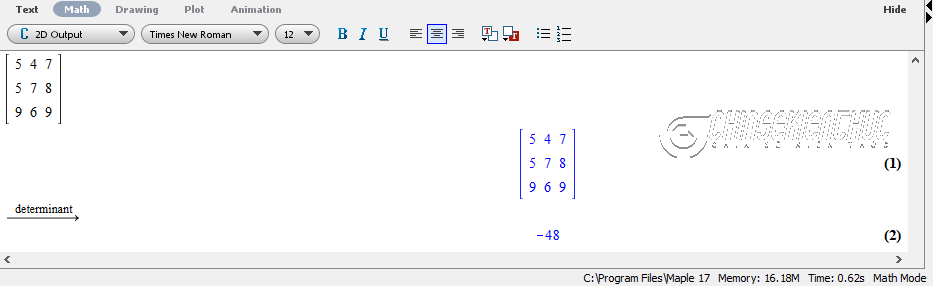
Bước 4. Giá trị tại dòng determinant chính là định thức của ma trận vừa nhập.
Nhận xét:
Phần mềm Maple có thể tính được định thức của ma trận vuông cấp bất kì và rất nhiều ứng dụng khác nữa.
II. Lời kết
Vâng, như vậy là mình đã hướng dẫn xong cho các bạn 4 cách tính định thức của ma trận cấp ba rồi ha.
Khi được yêu cầu tính định thức của ma trận vuông cấp 3×3 …
- Nếu cho dưới dạng tự luận thì bạn có thể áp dụng Cách 2, Cách 3, Cách 4 của Phương pháp 1
- Nếu cho dưới dạng trắc nghiệm thì áp dụng phương pháp máy tính CASIO fx-580VN X.
Các bạn hãy linh hoạt áp dụng nhé. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Hướng dẫn 4 cách xét dấu của tam thức bậc hai (có ví dụ)
- Cách cộng, trừ, nhân và chia số phức (có nhiều ví dụ)
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống