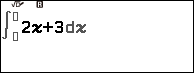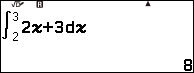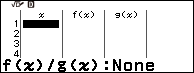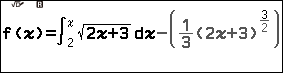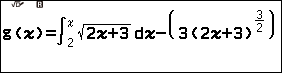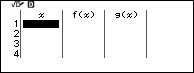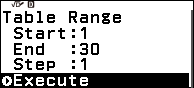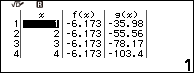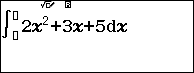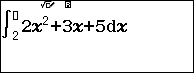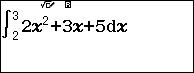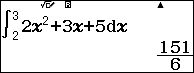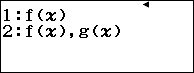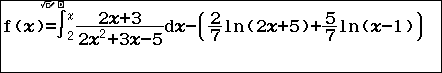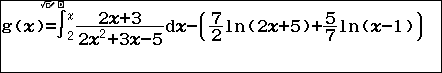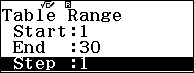Vâng, trong Toán học thì tích phân có khá nhiều loại khác nhau, có thể kể đến như tích phân xác định (1), tích phân không xác định (nguyên hàm) (2), tích phân suy rộng (3), tích phân bội hai (4), tích phân bội ba (5), tích phân mặt (6), tích phân đường(7), …
Tuy nhiên, trong phạm vi ngắn gọn của bài viết này thì chúng ta chỉ tìm hiểu về cách sử dụng máy tính CASIO để tính hai loại tích phân đầu tiên thôi ha.
Loại thứ ba (tích phân suy rộng) nếu có điều kiện mình sẽ hướng dẫn các bạn trong một bài viết khác.
Các loại tích phân còn lại không tính được bằng máy tính CASIO nên mình sẽ không đề cập đến ha.
Muốn tính được bạn cần sử dụng kiến thức Toán học, hoặc phần mềm Maple và dịch vụ trực tuyến Wolfram Alpha.
Mục Lục Nội Dung
#1. Cách tính tích phân trên Casio fx 880 BTG
Ví dụ 1. Tính tích phân $\int_2^3 2x+3 dx$
Bước 1. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Integration => nhấn phím OK


Bước 2. Nhập hàm số dưới dấu tích phân 2x+3
Bước 3. Nhấn phím => nhập cận trên 3
Bước 4. Nhấn phím => nhập cận dưới 2
Bước 5. Nhấn phím EXE
Vậy tích phân đã cho bằng 8
Chú ý.
Cài đặt đơn vị góc là ra đi an nếu hàm số dưới dấu tích phân có chứa các hàm lượng giác sin, cos, tan và cot.
Ví dụ 2. Nguyên hàm của hàm số $\int \sqrt{2x+3} dx$ bằng
A. $\frac{1}{3}(2x+3)^{\frac{3}{2}}$
B. $3(2x+3)^{\frac{3}{2}}$
C. $\frac{1}{3}(2x+3)^{\frac{2}{3}}$
D. $3(2x+3)^{\frac{2}{3}}$
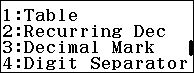
Bước 1. Nhấn phím HOME => chọn Table => nhấn phím OK

Bước 2. Nhấn phím TOOLS => chọn Table Type => nhấn phím OK => chọn f(x) / g(x) => nhấn phím OK => nhấn phím AC
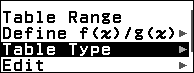
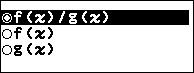
Chú ý.
Bước 2 bạn không cần thực hiện nữa nếu như bảng giá trị Table của bạn đã có sẵn hai hàm f(x) và g(x)
Bước 3.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Bước 3.1. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK
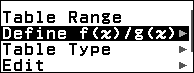
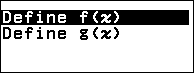
Bước 3.2. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Integration => nhấn phím OK => nhập $\int_2^x \sqrt{2x+3}dx-\left(\frac{1}{3}(2x+3)^{\frac{3}{2}}\right)$


Chú ý.
$\frac{1}{3}(2x+3)^{\frac{3}{2}}$ là hàm số của phương án A
Bước 3.3. Nhấn phím OK
Bước 4.
Bước 4.1. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define g(x) => nhấn phím OK
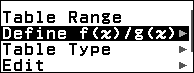
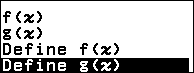
Bước 4.2. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Integration => nhấn phím OK => nhập $\int_2^x \sqrt{2x+3}dx-\left(3(2x+3)^{\frac{3}{2}}\right)$


Chú ý.
$3(2x+3)^{\frac{3}{2}}$ là hàm số của phương án B
Bước 4.3. Nhấn phím OK
Chú ý.
Cận dưới là một giá trị bất kì thuộc tập xác định của hàm số dưới dấu tích phân.
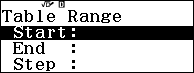
Bước 5. Nhấn phím TOOLS => chọn Table Range => nhấn phím OK => nhập 1 => nhấn phím EXE => nhập 30 => nhấn phím EXE => nhập 1 => nhấn phím EXE
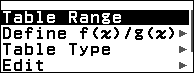
Bước 6. Nhấn phím EXE
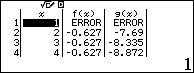
Quan sát bảng giá trị Table vừa tạo, hàm nào cho giá trị giống nhau thì phương án tương ứng chính là đáp án cần tìm.
Dễ thấy phương án A là đáp án của bài toán đã cho.
Chú ý.
Nếu không có hàm nào cho giá trị giống nhau thì bạn hãy định nghĩa lại hàm f(x) và g(x) với phương án C và D.
#2. Cách tính tích phân trên fx 580 VN X
Ví dụ 3. Tính tích phân $\int_2^3 2x^2+3x+5 dx$
Bước 1. Nhấn phím
Bước 2.
Bước 2.1. Nhập hàm số dưới dấu tích phân $2x^2+3x+5$
Bước 2.2. Nhấn phím => nhập cận dưới 2
Bước 2.3. Nhấn phím => nhập cận trên 3
Bước 3. Nhấn phím =
Vậy tích phân đã cho bằng $\frac{151}{6}$
Ví dụ 4. Nguyên hàm của hàm số $\int \frac{2x+3}{2x^2+3x-5} dx$
A. $\frac{2}{7}\ln(2x+5)+\frac{5}{7}\ln(x-1)$
B. $\frac{7}{2}\ln(2x+5)+\frac{5}{7}\ln(x-1)$
C. $\frac{2}{7}\ln(2x+5)+\frac{7}{5}\ln(x-1)$
D. $\frac{7}{2}\ln(2x+5)+\frac{7}{5}\ln(x-1)$
Bước 1. Nhấn phím SHIFT => nhấn phím MENU => nhấn phím => nhấn phím
=> nhấn phím 1 => nhấn phím 2


Bước 2. Nhấn phím MENU => chọn Table => nhấn phím =

Bước 3.
Bước 3.1 Nhấn phím => nhập $\int_2^x \frac{2x+3}{2x^2+3x-5}dx-\left(\frac{2}{7}\ln(2x+5)+\frac{5}{7}\ln(x-1)\right)$
Bước 3.2. Nhấn phím =
Bước 4.
Bước 4.1. Nhấn phím => nhập $\int_2^x \frac{2x+3}{2x^2+3x-5}dx-\left(\frac{7}{2}\ln(2x+5)+\frac{5}{7}\ln(x-1)\right)$
Bước 4.2. Nhấn phím =
Bước 5. Nhập 1 => nhấn phím = => nhập 30 => nhấn phím = => nhập 1 => nhấn phím =
Bước 6. Nhấn phím =
Quan sát bảng giá trị Table vừa tạo, hàm nào cho giá trị giống nhau thì phương án tương ứng chính là đáp án cần tìm.
Dễ thấy phương án A là đáp án của bài toán đã cho.
Chú ý.
Nếu có một hoặc một vài giá trị của cột f(x) hoặc g(x) bị lỗi ERROR thì vẫn không ảnh hưởng đến kết quả.
#3. Lời kết
Okay, trên đây là chi tiết các bước tính tích phân xác định và tích phân không xác định (nguyên hàm) bằng máy tính CASIO fx 580 VNX và 880 BTG..
Máy tính dù có hiện đại đến đâu thì nó cũng chỉ là công cụ, giúp chúng ta kiểm tra kết quả là chính.
Vậy nên bạn vẫn cần phải nắm vững kiến thức Toán học nếu muốn vươn cao bay xa bạn nhé >.<
Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
Đọc thêm:
- Tích phân là gì? 2 cách tính tích phân đơn giản nhất
- Cách tính tích phân suy rộng bằng máy Casio 580 & 880
- Cách tính diện tích của hình, thể tích của vật bằng tích phân
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống