Cách tính diện tích của hình, thể tích của vật bằng tích phân

Trong thực tiễn cuộc sống, nhiều trường hợp chúng ta phải thực hiện tính diện tích của những hình phẳng, hay thể tích của những vật thể phức tạp.

Chẳng hạn như:

• Khi xây dựng một nhà máy thuỷ điện chúng ta phải tính diện tích thiết diện ngang của dòng sông.
• Hoặc khi đóng tàu các kĩ sư cần xác định thể tích của khoang tàu…

Tuy nhiên, diện tích và thể tích vừa trình bày không thể tính chính xác được nếu chỉ sử dụng các kiến thức của hình học Euclid.

Vậy nên các nhà Toán học đã nghiên cứu và cho ra đời phép tính tích phân.

Và trong bài viết ngày hôm nay chúng ta sẽ cùng nhau tìm hiểu về cách tính diện tích của hình phẳng và thể tích của một vật thể bằng tích phân nhé.

#1. Tính diện tích hình phẳng

+) Nếu hàm số $y=f(x)$ liên tục trên đoạn $[a ; b]$ thì diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=a, x=b$ sẽ bằng $\int_a^b|f(x)| dx$

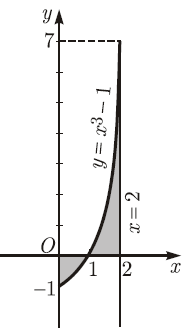
Ví dụ 1. Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y=x^3-1$, đường thẳng $x=2$, trục tung và trục hoành.

Lời giải:

Đặt $f(x)=x^3-1$

Chúng ta thấy $f(x) \leq 0$ trên $[0 ; 1]$ và $f(x) \geq 0$ trên $[1 ; 2]$

Áp dụng công thức $\int_a^b|f(x)| dx$ chúng ta được diện tích $S$ của hình đang xét sẽ bằng

$=\int_0^2\left|x^3-1\right|dx$

$=\int_0^1\left(1-x^3\right) dx+\int_1^2\left(x^3-1\right) dx$

$=\frac{3}{4}+\frac{11}{4}=\frac{7}{2}$

+) Muốn tính được diện tích $S$ của hình phẳng giới hạn bởi đồ thị các hàm số $y=f(x)$, $y=g(x)$ liên tục trên đoạn $[a; b]$ và hai đường thẳng $x=a, x=b$ chúng ta cần sử dụng công thức sau $\int_a^b|f(x)-g(x)| dx$

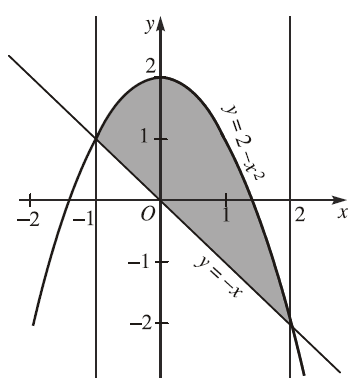
Ví dụ 2. Tính diện tích $S$ của hình phẳng giới hạn bởi đường cong parabol $y=2-x^2$ và đường thẳng $y=-x$

Lời giải:

Đầu tiên, chúng ta cần tìm hoành độ giao điểm của các đồ thị của hai hàm số đã cho bằng cách giải phương trình $2-x^2=-x$

Dễ thấy phương trình bậc hai một ẩn $2-x^2=-x$ có hai nghiệm là $x=-1$ và $x=2$

Hình phẳng đang xét giới hạn bởi các đồ thị của các hàm số $y=2-x^2, y=-x$ và hai đường thẳng $x=-1, x=2$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Áp dụng công thức $\int_a^b|f(x)-g(x)| dx$ chúng ta có $S=\int_{-1}^2\left(2+x-x^2\right) dx=\left.\left(2 x+\frac{x^2}{2}-\frac{x^3}{3}\right)\right|_{-1} ^2=\frac{9}{2}$

+) Muốn tính được diện tích các hình phẳng phức tạp hơn thì chúng ta phải chia hình đã cho thành một số hình đơn giản mà ta đã biết cách tính diện tính.

#2. Tính thể tích của vật

Trong không gian với hệ tọa độ $Oxyz$ cho một vật thể. Gọi:

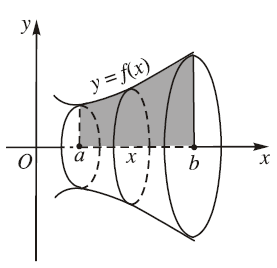
• $B$ là phần của vật thể giới hạn bởi hai mặt phẳng vuông góc với trục $Ox$ tại các điểm $a$ và $b$
• $S(x)$ là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x(a \leq x \leq b)$

Giả sử $S=S(x)$ là một hàm số liên tục

Các nhà Toán học đã chúng minh được rằng thể tích $V$ của $B$ sẽ bằng $\int_a^b S(x) dx$

Công việc cũng chúng ta chỉ cần áp dụng công thức vừa trình bày sẽ tìm được thể tích của một số vật thể quen thuộc.

#3. Tính thể tích của khối tròn xoay

Một hình phẳng quay xung quanh một trục nào đó tạo nên một khối tròn xoay.

Cho hàm số $y=f(x)$ liên tục, không âm trên $[a ; b]$

Lúc bấy giờ hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, trục hoành và hai đường thẳng $x=a$, $x=b$ quay quanh trục hoành tạo nên một khối tròn xoay.

Thể tích $V$ của khối tròn xoay được tính theo công thức: $\pi \int_a^b f^2(x) dx$

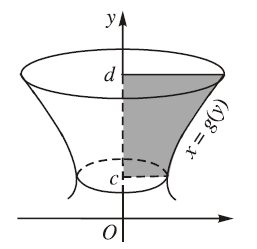
Cho đường cong có phương trình $x=g(y)$ với  $g$ là hàm số liên tục và không âm trên đoạn $[c ; d]$

Lúc này hình phẳng giới hạn bởi đường cong $x=g(y)$, trục tung và hai đường thẳng $y=c, y=d$, quay quanh trục tung tạo nên một khối tròn xoay.

Thể tích $V$ của khối tròn xoay được tính theo công thức $\pi \int_c^d g^2(y) dy$

#4. Lời kết

Muốn tính được diện tích của hình phẳng và thể tích của vật thể thì ngoài các kiến thức vừa được trình bày bên trên ra, bạn cũng nên xem thêm các kiến thức về:

• Cách tính nguyên hàm
• Cách tính tích phân
• Cách giải phương trình đa thức (bậc nhất, bậc hai, …)
• Cách vẽ đồ thị của một số hàm số thường gặp.

Chúc các bạn học tốt, còn bây giờ xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tính diện tích và thể tích của hình trụ (có ví dụ)
• Cách tính diện tích và thể tích của hình nón, hình nón cụt
• Cách tính diện tích tam giác trên mặt phẳng và trong không gian

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn