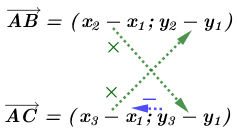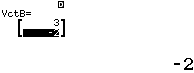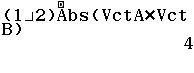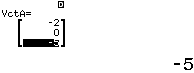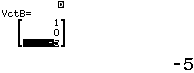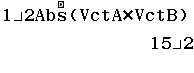Cách tính diện tích tam giác trên mặt phẳng và trong không gian

Xin chào tất cả các bạn, hôm nay mình sẽ tiếp tục hướng dẫn cho các bạn cách tính diện tích tam giác trên mặt phẳng và cách tính diện tích tam giác trong không gian.

Vì muốn các bạn học sinh cũng có thể hiểu được nên mình sẽ không trình bày thông qua ma trận, định thức. Mà thay vào đó, mình sẽ trình bày chi tiết cho các bạn cách tính luôn.

Đây là một ưu điểm, nhưng cũng là nhược điểm của phương pháp trình bày này, nhược điểm là làm cho các công khá dài dòng.

Tuy nhiên, đó không phải là vấn đề nếu như bạn chịu khó xem, đọc kỹ, thực hành nhiều lần và có sự hỗ trợ của máy tính CASIO fx-580VN X (nếu mẹ bạn chưa mua cho thì có thể sử dụng phiên bản giả lập này :V)

I. Cách tính diện tích tam giác nằm trên mặt phẳng 

#1. Thuật toán

Tính diện tích tam giác ABC biết $A=(x_1; y_1), B=(x_2; y_2), C=(x_3; y_3)$

Bước 1. Tính $\overrightarrow{AB}, \overrightarrow{AC}$

$\overrightarrow{AB}=(x_2-x_1; y_2-y_1), \overrightarrow{AC}=(x_3-x_1; y_3-y_1)$

Bước 2. Tính giá trị biểu thức $(x_2-x_1).( y_3-y_1)- (x_3-x_1).( y_2-y_1)$

Bước 3. Tính giá trị biểu thức $\frac{1}{2}|(x_2-x_1).( y_3-y_1)- (x_3-x_1).( y_2-y_1)|$

#2. Bình luận chút về thuật toán

• Nếu là câu hỏi dạng trắc nghiệm thì bạn chỉ cần thực hiện Bước 3
• Nếu là câu hỏi tự luận thì bạn có thể dựa theo ba bước trên để trình bày lời giải (trình bày như sách giáo khoa)
• Bản chất của Bước 2 chính là cách tính định thức của ma trận vuông cấp $2 \times 2$

#3. Ví dụ minh họa về cách tính diện tích tam giác trên mặt phẳng

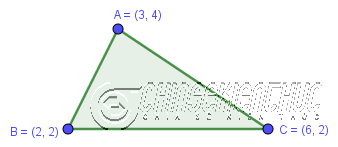
Tính diện tích tam giác ABC biết điểm $A=(3; 4), B=(2; 2), C=(6; 2)$

Lời Giải:

Bước 1. Tính $\overrightarrow{AB}, \overrightarrow{AC}$

$\overrightarrow{AB}=(-1;-2), \overrightarrow{AC}=(3;-2)$

Bước 2. Tính giá trị biểu thức $(-1).(-2)-3.(-2)=8$

Bước 3. Tính giá trị biểu thức $\frac{1}{2}.|8|=4$

=> Vậy diện tích tam giác ABC bằng 4 ĐVDT

#4. Thủ thuật tính nhanh diện tích tam giác trên mặt phẳng bằng CASIO FX-580VN X

Bước 1. Chọn phương thức tính toán Vector

Bước 2. Gán véc-tơ $\overrightarrow{AB}, \overrightarrow{AC}$ lần lượt vào các véc-tơ VctA, VctB

Bước 3. Tính giá trị biểu thức $\frac{1}{2}Abs(VctA \times VctB)$

II. Cách tính diện tích tam giác nằm trong không gian

#1. Cách tính tích có hướng của hai véc-tơ

Cho $\vec{u}=(x; y; z), \vec{v}=(x’; y’;z’)$ khi đó tính tích có hướng của $\vec{u}$ và $\vec{v}$ sẽ được tính theo công thức $(yz’-y’z; zx’-z’x; xy’-x’y)$

Chú ý:

• Tích có hướng của $\vec{v}$ và $\vec{v}$ thường được kí hiệu là $[\vec{u}; \vec{v}]$
• Tích có hướng của hai véc-tơ là một véc-tơ

#2. Cách tính độ dài véc-tơ

Cho $\vec{u}=(x; y; z)$ khi đó độ dài của $\vec{u}$ sẽ được tính theo công thức $\sqrt{x^2+y^2+z^2}$

Chú ý:

• Bạn có thể tính độ dài ba cạnh của tam giác rồi áp dụng công thức Heron để tính diện tích tam giác
• Độ dài của một véc-tơ là một số thực dương

#3. Thuật giải

Tính diện tích tam giác ABC biết $A=(x_1; y_1; z_1), B=(x_2; y_2; z_2), C=(x_3; y_3; z_3)$

Bước 1. Tính $\overrightarrow{AB}, \overrightarrow{AC}$

$\overrightarrow{AB}=(x_2-x_1; y_2-y_1; z_2-z_1), \overrightarrow{AC}=(x_3-x_1; y_3-y_1; z_3-z_1)$

Bước 2. Tính tích có hướng của $\overrightarrow{AB}$ và $\overrightarrow{AC}$

Bước 3. Tính độ dài của $[\overrightarrow{AB}; \overrightarrow{AC}]$

Bước 4. Tính giá trị biểu thức $\frac{1}{2}|[\overrightarrow{AB}; \overrightarrow{AC}]|$

#4. Ví dụ minh họa cho cách tính diện tích tam trong không gian

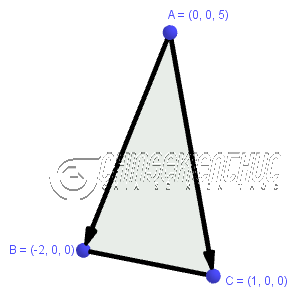
Tính diện tích tam giác ABC biết $A=(0; 0; 5), B=(-2; 0; 0), C=(1; 0; 0)$

Bước 1. Tính $\overrightarrow{AB}$ và $\overrightarrow{AC}$

$\overrightarrow{AB}=(-2; 0; -5), \overrightarrow{AC}=(1; 0; -5)$

Bước 2. Tính tích có hướng của $\overrightarrow{AB}$ và $\overrightarrow{AC}$

$[\overrightarrow{AB}; \overrightarrow{AC}]=(0; -15; 0)$

Bước 3. Tính độ dài của $[\overrightarrow{AB}; \overrightarrow{AC}]$

$|[\overrightarrow{AB}; \overrightarrow{AC}]|=15$

Bước 4. Tính giá trị biểu thức $\frac{1}{2}|[\overrightarrow{AB}; \overrightarrow{AC}]|=\frac{1}{2}.15=\frac{15}{2}$

=> Vậy diện tích của tam giác ABC bằng $\frac{15}{2}$ ĐVDT

#5. Tính diện tích tam giác trong không gian bằng CASIO fx-580VN X

Bước 1. Chọn phương thức tính toán Vector

Bước 2. Gán véc-tơ $\overrightarrow{AB}, \overrightarrow{AC}$ lần lượt vào các véc-tơ VctA, VctB

Bước 3. Tính giá trị biểu thức $\frac{1}{2}Abs(VctA \times VctB)$

III. Lời kết

Nếu các bạn tinh ý sẽ thấy, công thức tính diện tích tam giác trên mặt phẳng chính là trường hợp đặc biệt của công thức tính diện tích tam giác trong không gian nha các bạn.

Như vậy, thay vì phải nhớ đến hai công thức thì bạn chỉ cần nhớ một công thức duy nhất.

Mẹo để nhớ được công thức tính diện tích tam giác trong không gian chính là nhớ câu nửa độ dài tích có hướng.

Ngoài ra, nếu cần tính diện tích hình bình hành có tọa độ ba điểm hoặc tọa độ của hai véc-tơ thì bạn cũng áp dụng công thức trên nhưng nhớ nhân thêm 2 ở kết quả sau cùng nhé.

Hi vọng những kiến thức trong bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Cách tính diện tích mặt cầu và thể tích hình cầu (có ví dụ)
• Cách tính thể tích tứ diện trong không gian (công thức & casio)
• Cách tính diện tích tam giác thường, vuông, cân và tam giác đều

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com