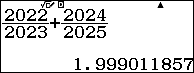Tiếp nối mạch kiến thức về phân số, hôm nay mình sẽ hướng dẫn các bạn cách cộng hai phân số bất kỳ bằng 3 cách khách nhau.
Tương tự như những bài viết trước thì đầu tiên, mình sẽ trình bày về lý thuyết, tiếp theo là cho ví dụ minh họa và cuối cùng là thủ thuật cộng hai phân số bằng máy tính CASIO.
Mục Lục Nội Dung
Cách #1. Cộng hai phân số bất kỳ (sử dụng kiến thức Toán học)
1. Quy trình giải
Bước 1. Rút gọn phân số nếu các phân số đã cho chưa tối giản.
Bước 2. Quy đồng mẫu số nếu các phân số đã cho không cùng mẫu.
Bước 3. Tiến hành cộng các phân số theo quy tắc, cộng các tử và giữ nguyên mẫu.
Bước 4. Rút gọn phân số sau khi cộng (nếu có thể).
2. Bài tập ví dụ
Ví dụ 1. Cộng hai phân số $\frac{2}{3}$ và $\frac{5}{3}$
Quan sát hai phân số đã cho ta thấy chúng đều là phân số tối giản và có cùng mẫu nên không cần thực hiện Bước 1 và Bước 2
Lời giải:
$\frac{2}{3}+\frac{5}{3}=\frac{2+5}{3}=\frac{7}{3}$
Ví dụ 2. Cộng hai phân số $\frac{7}{11}$ và $\frac{13}{17}$
Quan sát hai phân số đã cho ta thấy chúng đều là phân số tối giản nhưng không cùng mẫu nên chúng ta cần thực hiện Bước 2, tức là chúng ta sẽ thực hiện quy đồng mẫu số trước.
Lời giải:
Quy đồng mẫu số:
+) Bội chung nhỏ nhất của 11 và 17 là 187.
+) Thừa số phụ
$187:11=17; 187:17=11$
+) Lần lượt nhân tử và mẫu của $\frac{7}{11}, \frac{13}{17}$ với từng thừa số phụ tương ứng.
$\frac{7}{11}=\frac{7.17}{11.17}=\frac{119}{187}$
$\frac{13}{17}=\frac{13.11}{17.11}=\frac{143}{187}$
Suy ra $\frac{119}{187}+\frac{143}{187}=\frac{119+143}{187}=\frac{262}{187}$
Vậy $\frac{7}{11}+\frac{13}{17}=\frac{262}{187}$
Ví dụ 3. Cộng hai phân số $\frac{14}{22}$ và $\frac{39}{51}$
Quan sát hai phân số đã cho ta thấy chúng chưa tối giản nên cần thực hiện Bước 1 tức rút gọn trước.
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Lời giải:
Rút gọn phân số:
$\frac{14}{22}$
$UCLN(14,22)=2$
Suy ra $\frac{14:2}{22:2}=\frac{7}{11}$
$\frac{39}{51}$
$UCLN(39,51)=3$
Suy ra $\frac{39:3}{51:3}=\frac{13}{17}$
Phần lời giải tiếp theo hoàn toàn tương tự như Ví dụ 2
Ví dụ 4. Cộng các phân số $\frac{2}{3}, \frac{5}{7}$ và $\frac{14}{22}$
Lời giải:
Rút gọn phân số $\frac{14}{22}$
$\frac{14}{22}$
$UCLN(14,22)=2$
Suy ra $\frac{14:2}{22:2}=\frac{7}{11}$
Quy đồng mẫu số ba phân số $\frac{2}{3}, \frac{5}{7}$ và $\frac{7}{11}$
$BCNN(3,7,11)=231$
Thừa số phụ:
$231:3=77; 231:7=33; 231:11=21$
Lần lượt nhân tử và mẫu của $\frac{2}{3}, \frac{5}{7}$ và $\frac{7}{11}$ với từng thừa số phụ tương ứng
$\frac{2}{3}=\frac{2.77}{3.77}=\frac{154}{231}, \frac{5}{7}=\frac{5.33}{7.33}=\frac{165}{231}$ và $\frac{7}{11}=\frac{7.21}{11.21}=\frac{147}{231}$
Suy ra $\frac{154}{231}+\frac{165}{231}+\frac{147}{231}=\frac{154+165+147}{231}=\frac{466}{231}$
Vậy $\frac{2}{3}+\frac{5}{7}+\frac{14}{22}=\frac{466}{231}$
Cách #2. Cách cộng hai phân số bất kỳ (sử dụng máy tính CASIO)
Trong bài viết này thì mình sẽ sử dụng máy tính CASIO fx-580VN X nhé !
Ưu điểm của phương pháp này là nhanh chóng, chính xác, cho dù các phân số cần cộng có tối giản hay không tối giản, cùng mẫu hay không cùng mẫu
Chú ý:
Tổng sau khi cộng sẽ tự động được rút gọn
Nhược điểm là tổng sau khi cộng không hiển thị được dưới dạng $\frac{a}{b}$ nếu tử và mẫu của các phân số cần cộng có giá trị quá lớn.
Ví dụ 5. Cộng các phân số $\frac{2}{3}, \frac{5}{7}$ và $\frac{14}{22}$
Bước 1. Nhấn …
để nhập $\frac{2}{3}+\frac{5}{7}+\frac{14}{22}$
Bước 2. Nhấn để xem kết quả
Ví dụ 6. Cộng các phân số $\frac{2022}{2023}$ và $\frac{2024}{2025}$
Xem video thao tác:
Tổng không hiển thị được dưới dạng $\frac{a}{b}$ vì các tử số và mẫu số của hai phân số này có giá trị vượt quá khả năng tính toán của máy tính CASIO
Giải pháp là chúng ta sẽ giải bằng kiến thức Toán học hoặc công cụ trực tuyến Wolfram Alpha.
Cách #3. Giải bằng công cụ trực tuyến Wolfram Alpha
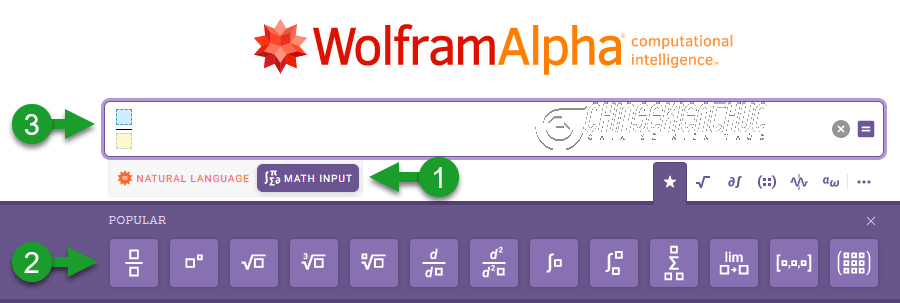
Bước 1. Truy cập vào trang chủ của dịch vụ theo địa chỉ https://www.wolframalpha.com/
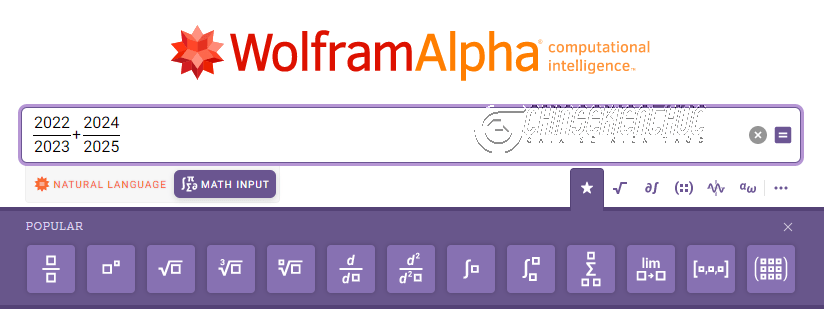
Bước 2. Chọn MATH INPUT => nhấn chọn biểu tượng => rồi nhập phân số thứ nhất.
Bước 3. Nhấn phím + trên bàn phím máy tính => chọn biểu tượng => nhập tiếp phân số thứ 2
Bước 4. Nhấn phím Enter trên bàn phím máy tính để xem kết quả, giá trị tại dòng Exact result chính là giá trị cần tìm..
Lời kết
Okay, trên đây là 3 cách cộng hai phân số mà mình muốn chia sẻ đến các bạn.
Thuật toán cộng các phân số được mình trình bày trong bài viết này về bản chất hoàn toàn tương tự với sách giáo khoa.
Chỉ khác nhau là mình không chia thành trường hợp cùng mẫu và không cùng mẫu mà thôi.
Khi được yêu cầu cộng các phân số thì bạn hãy quan sát kỹ các phân số đã cho rồi thực hiện cho chính xác ha.
Chẳng hạn nếu các phân số đã cho đều đã được rút gọn thành phân số tối giản rồi thì không cần thực hiện Bước 1 nữa, kiểu kiểu như vậy … Hãy linh hoạt áp dụng nha các bạn.
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống