Cách vẽ tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều

Hôm nay chúng ta sẽ cùng nhau tìm hiểu cách vẽ các đa giác đều thường gặp, như là tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều.

Tương ứng với mỗi một đa giác đều thì mình sẽ hướng dẫn một hoặc một vài cách vẽ, cũng như  cách dựng khác nhau.

Mỗi cách vẽ/ cách dựng sẽ sử dụng các công cụ khác nhau, vì vậy bạn cần chuẩn bị đầy đủ thước thẳng, compa và thước đo góc nếu muốn thực hành tất cả các cách trong bài hướng dẫn này nhé.

#1. Cách vẽ tam giác đều

Phương pháp 1. Chỉ sử dụng thước thẳng

Bước 1. Vẽ đoạn thẳng BC

Bước 2. Vẽ đường trung trực của đoạn thẳng BC

Bước 2.1. Vẽ trung điểm M

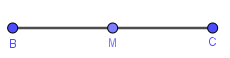
Bước 2.2. Vẽ đường thẳng (d) đi qua M và vuông góc BC

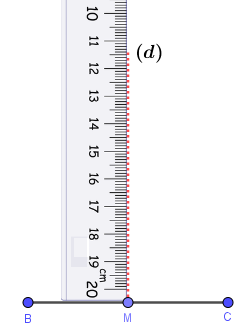
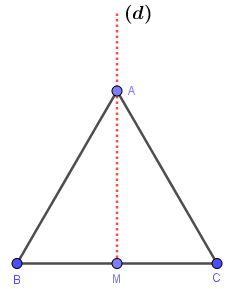
Bước 3. Vẽ điểm A trên (d) sao cho BA = BC

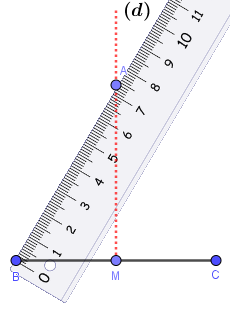
Bước 4. Vẽ đoạn thẳng BA, CA

Phương pháp 2. Sử dụng thước thẳng và compa

Bước 1. Vẽ cạnh BC

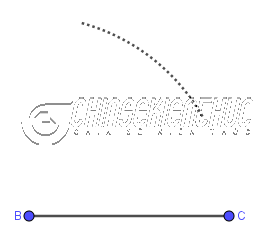
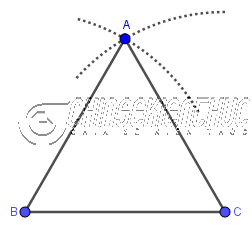
Bước 2. Vẽ đường tròn/ cung tròn tâm B bán kính BC

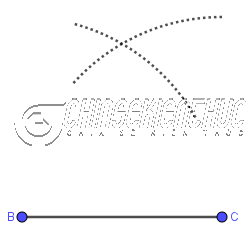
Bước 3. Vẽ đường tròn/ cung tròn tâm C bán kính CB

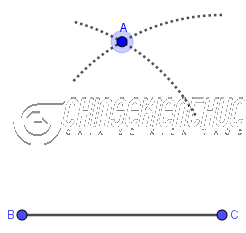
Bước 4. Vẽ giao điểm A của hai đường tròn/ cung tròn

Bước 5. Vẽ các đoạn thẳng BA, CA

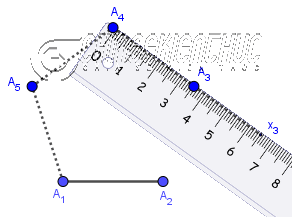
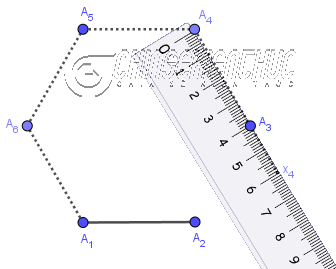
Phương pháp 3. Sử dụng thước thẳng và thước đo góc

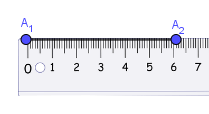
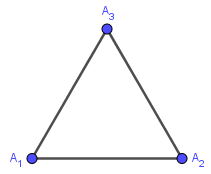
Bước 1. Vẽ đoạn thẳng $A_1A_2$

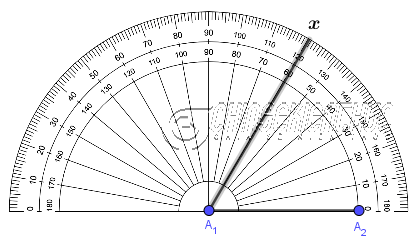
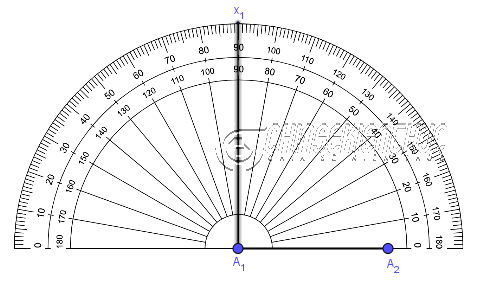
Bước 2. Vẽ $\widehat{A_2A_1x}=60^o$

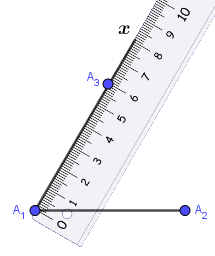
Bước 3. Trên tia $A_1x$ vẽ điểm $A_3$ sao cho $A_1A_3=A_1A_2$

Bước 4. Vẽ các đoạn thẳng $A_2A_3, A_3A_1$

#2. Cách vẽ tứ giác đều và hình vuông

Phương pháp 1. Sử dụng thước thẳng và compa

Phương pháp này khá phức tạp, không có nhiều ứng dụng trong thực tiễn, vì vậy mình không hướng dẫn.

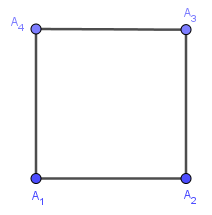
Phương pháp 2. Sử dụng thước thẳng và thước đo góc

Bước 1. Vẽ đoạn thẳng $A_1A_2$

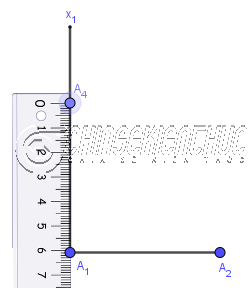
Bước 2. Vẽ $\widehat{A_2A_1x_1}=90^o$

Bước 3. Trên tia $A_1x_1$ vẽ điểm $A_4$ sao cho $A_1A_4=A_1A_2$

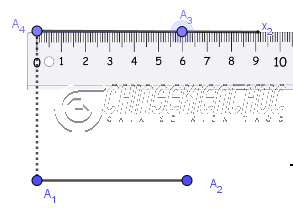
Bước 4. Thực hiện tương tự Bước 2 và Bước 3 để vẽ điểm $A_3$

Bước 5. Vẽ các đoạn thẳng $A_2A_3, A_3A_4, A_4A_1$

#3. Cách vẽ ngũ giác đều

Phương pháp 1. Sử dụng thước thẳng và compa

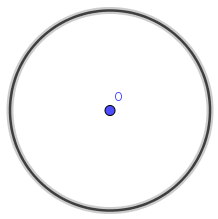
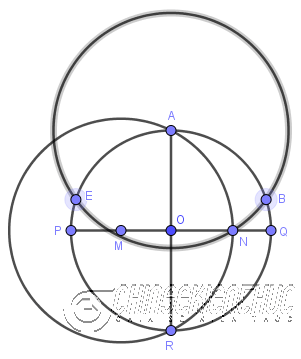
Bước 1. Vẽ đường tròn tâm O

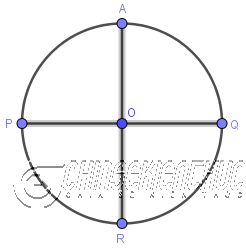
Bước 2. Vẽ đường kính AR và PQ (AR vuông góc PQ tại O)

Bước 3 …

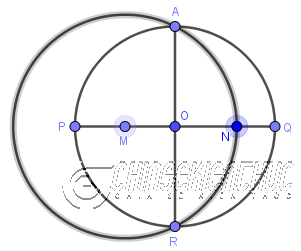
• Vẽ M là trung điểm PO
• Vẽ đường tròn tâm M bán kính MA, đường tròn này cắt OQ tại N

Bước 4. Vẽ đường tròn tâm A bán kính AN, đường tròn này cắt đường tròn tâm O tại E, B

Bước 5. Vẽ đường tròn tâm B bán kính BA, đường tròn này cắt đường tròn O tại C

Bước 6. Vẽ đường tròn tâm E bán kính EA, đường tròn này cắt đường tròn O tại D

Bước 7. Vẽ các đoạn thẳng AB, BC, CD, DE, EA

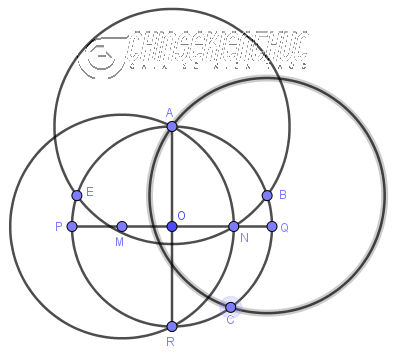
Phương pháp 2. Sử dụng thước thẳng và thước đo góc

Thực hiện tương tự các bước vẽ tứ giác đều với $\widehat{A_2A_1A_5}=108^o$

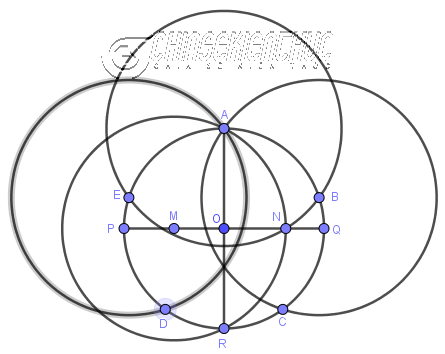
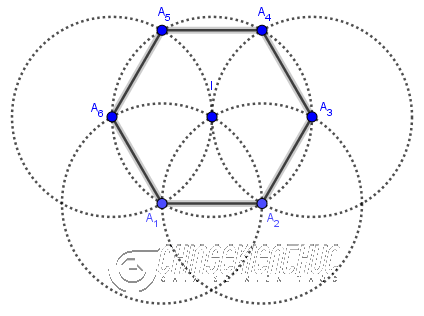
#4. Cách vẽ lục giác đều

Phương pháp 1. Vẽ bằng thước thẳng và compa

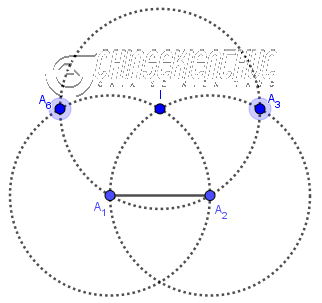
Bước 1. Vẽ đoạn thẳng $A_1A_2$

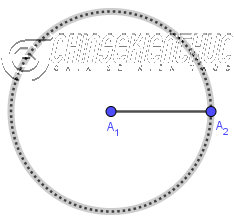
Bước 2. Vẽ đường tròn tâm $A_1$ bán kính $A_1A_2$

Bước 3. Vẽ đường tròn tâm $A_2$ bán kính $A_2A_1$

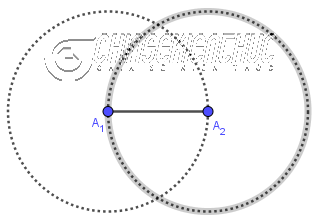
Bước 4. Vẽ giao điểm I của hai đường tròn ở Bước 2 và Bước 3

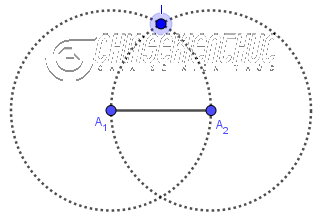
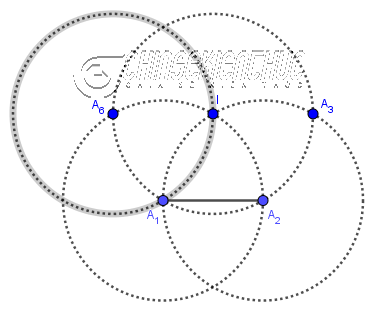
Bước 5. Vẽ đường tròn tâm I bán kính $IA_1$

Bước 6. Vẽ giao điểm $A_6$ và $A_3$ của đường tròn tâm I với hai đường tròn Bước 2 và Bước 3

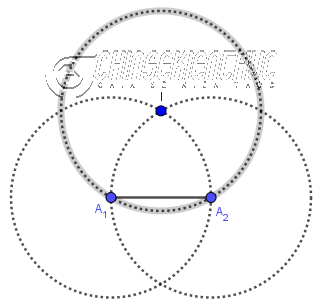
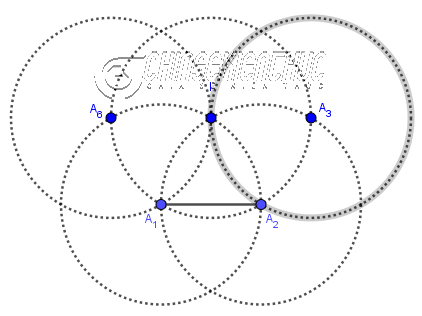
Bước 7. Vẽ đường tròn tâm $A_6$ bán kính $A_6 I$

Bước 8. Vẽ đường tròn tâm $A_3$ bán kính $A_3 I$

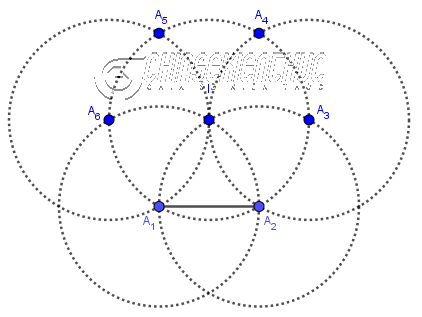
Bước 9. Vẽ giao điểm $A_5, A_4$ của hai đường tròn ở Bước 7, Bước 8 và đường tròn tâm I

Bước 10. Vẽ các đoạn thẳng $A_2A_3, A_3A_4, A_4A_5, A_5A_6, A_6A_1$

Phương pháp 2. Vẽ bằng thước thẳng và thước đo góc

Thực hiện tương tự các bước vẽ tứ giác đều với $\widehat{A_2A_1A_6}=180^o$

#5. Lời kết

Vâng, như vậy là mình đã hướng dẫn xong cho bạn cách vẽ tam giác đều, tứ giác đều, ngũ giác đều và lục giác đều bằng rất nhiều cách rồi ha.

Chúng ta nên phân biệt cụm từ vẽ hình và dựng hình hay công cụ được sử dụng khi vẽ hình và công cụ được sử dụng khi dựng hình.

• Vẽ hình có thể sử dụng thước thẳng, thước độ góc, compa, …
• Dựng hình chỉ có thể sử dụng thước thẳng và compa

Nếu là vẽ hình thì có thể vẽ được tất cả các đa giác đều.

Còn nếu là dựng hình thì không thể dựng được tất cả, dễ thấy nhất là thất giác đều. Tuy nhiên, đa giác đều nào dựng được thì chắc chắn là rất chính xác, có thể chứng minh cách dựng là bằng Toán học.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Vẽ tia phân giác của một góc đơn giản với 5 cách sau đây
• 3 cách vẽ trung điểm của đoạn thẳng mà mình hay áp dụng

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com