Xin chào tất cả các bạn, nội dung bài viết ngày hôm nay chúng ta sẽ cùng nhau tìm hiểu về các hệ thức lượng trong tam giác vuông nha.
Các hệ thức này sẽ giúp bạn tính được độ dài các cạnh và các góc của tam giác nếu biết độ dài hai cạnh hoặc độ lớn một cạnh và một góc nhọn.
Mảng kiến thức này tuy không có gì phức tạp nhưng mình vẫn quyết định trình bày chi tiết nhất có thể, vì đây là nền tảng kiến thức khá quan trọng trong suốt quá trình học.
Đầu tiên mình sẽ phát biểu hệ thức bằng lời, vẽ hình, trình bày công thức và cuối cùng là cho ví dụ minh họa. Okay, let’s go..
Mục Lục Nội Dung
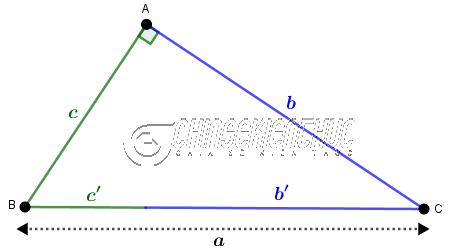
#1. Mối liên hệ giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
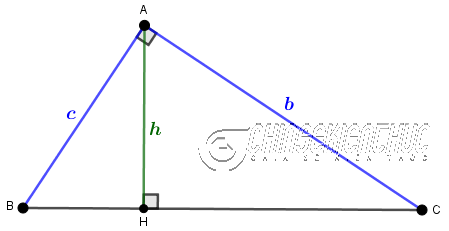
Hệ thức 1:
- Cách phát biểu thứ 1: Bình phương mỗi độ dài của cạnh góc vuông bằng tích của độ dài cạnh huyền và độ dài hình chiếu của cạnh góc vuông đó trên cạnh huyền.
$b^2=ab’, c^2=ac’$ HOẶC $b=\sqrt{ab’}, c=\sqrt{ac’}$
- Cách phát biểu thứ 2: Độ dài mỗi cạnh góc vuông bằng trung bình nhân của độ dài cạnh huyền và độ dài hình chiếu của cạnh góc vuông đó trên cạnh huyền.
#2. Các hệ thức liên quan đến đường cao
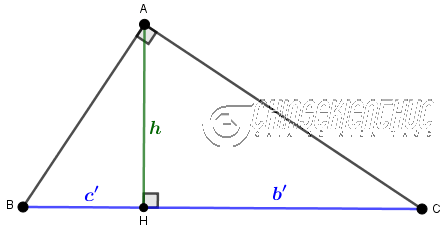
Hệ thức 2:
- Cách phát biểu 1: Bình phương độ dài đường cao ứng với cạnh huyền sẽ bằng tích của độ dài hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
$h^2=b’c’$ HOẶC $h=\sqrt{b’c’}$
- Cách phát biểu 2: Độ dài đường cao ứng với cạnh huyền bằng trung bình nhân độ dài hai đoạn thẳng mà nó định ra trên cạnh huyền.
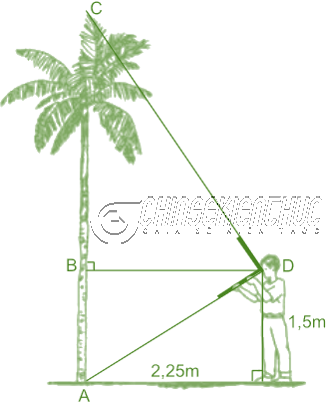
Ví dụ 1. Tính chiều cao của cây dừa, biết …
- Khoảng cách từ cây đến người đo bằng $2.25~m$
- Khoảng cách từ mắt của người đo đến mặt đất là $1.5~m$
- Mặt đất xung quanh cây và người do bằng phẳng.
Dễ thấy đây là một bài toán thực tế, muốn giải được bài toán này ta cần chuyển nó sang bài toán thuần túy Toán học.
- Chiều cao của cây là độ dài cạnh huyền $AC=AB+BC$
- Độ dài đường cao $BD=2.25~m$ (ứng với cạnh huyền CA) là khoảng cách từ cây đến người đo.
- Độ dài đoạn thẳng $AB=1.5~m$ là khoảng cách từ mắt của người đo đến mặt đất.
Lời giải:
Tam giác ADC vuông tại D, BD là đường cao ứng với cạnh huyền CA và AB là $1.5~m$
Suy ra $BD^2=AB.BC \Leftrightarrow (2.25)^2=1.5 \times BC \Rightarrow BC=\frac{(2.25)^2}{1.5}=3.375~m$
Suy ra $AC=AB+BC=3.375+1.5=4.875~m$
Vậy => chiều cao của cây dừa là $4.875~m$
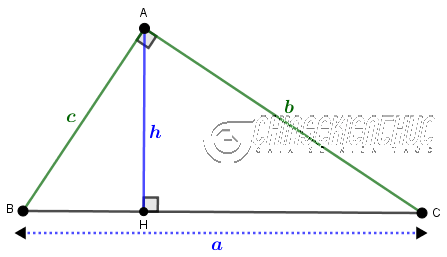
Hệ thức 3: Tích độ dài hai cạnh góc vuông bằng tích của độ dài cạnh huyền và độ dài đường cao tương ứng.
$bc=ah$
Hệ thức 4: Nghịch đảo của bình phương độ dài đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương độ dài hai cạnh góc vuông.
$\frac{1}{h^2}=\frac{1}{c^2}+\frac{1}{b^2}$
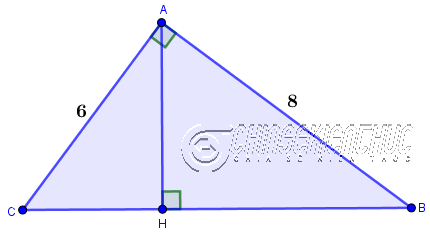
Ví dụ 2. Tính độ dài đường cao AH của tam giác ABC (vuông ở A) biết $AC=6, AB=8$
Lời giải:
Áp dụng Hệ thức 4 ta được $\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2} \Leftrightarrow \frac{1}{AH^2}=\frac{25}{576} \Leftrightarrow AH^2=\frac{576}{25}$
Suy ra $AH=\sqrt{\frac{576}{25}}=\frac{24}{5}=4.8$
Vậy => độ dài đường cao AH bằng 4.8 ĐVDD
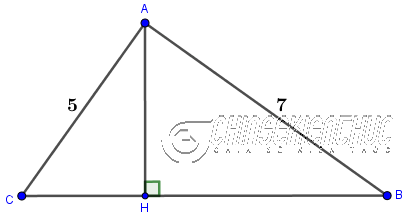
Ví dụ 3. Tính độ dài cạnh huyền BC, đường cao AH, đoạn thẳng CH và BH? Biết tam giác ABC có $\hat{A}=90^o, AC=5, AB=7$
Lời giải:
Độ dài cạnh huyền BC
Áp dụng định lí Pytago và tam giác vuông ABC ta được $BC^2=5^2+7^2$
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Suy ra $BC=\sqrt{5^2+7^2}=\sqrt{74} \approx 8.6$
Độ dài đường cao AH
Áp dụng Hệ thức 4 vào tam giác vuông ABC ta được $\frac{1}{AH^2}=\frac{1}{5^2}+\frac{1}{7^2} \Leftrightarrow \frac{1}{AH^2}=\frac{74}{1225} \Leftrightarrow AH^2=\frac{1225}{74}$
Suy ra $AH=\sqrt{\frac{1225}{74}}=\frac{35\sqrt{74}}{74} \approx 4.1$
Độ dài đoạn thẳng CH và BH
Cách 1. Áp dụng Hệ thức 1
- $AC^2=CB.CH \Leftrightarrow 5^2=\sqrt{74}.CH \Leftrightarrow CH=\frac{5^2}{\sqrt{74}}=\frac{25\sqrt{74}}{74} \approx 2.9$
- $AB^2=CB.BH \Leftrightarrow 7^2=\sqrt{74}.BH \Leftrightarrow BH=\frac{7^2}{\sqrt{74}}=\frac{49\sqrt{74}}{74} \approx 5.7$
Cách 2. Áp dụng định lý Pytago
- $CH^2=AC^2-AH^2 \Leftrightarrow CH^2=5^2-\left( \frac{35\sqrt{74}}{74} \right)^2 \Rightarrow CH=\frac{25\sqrt{74}}{74} \approx 2.9$
- $BH^2=AB^2-AH^2 \Leftrightarrow BH^2=7^2-\left( \frac{35\sqrt{74}}{74} \right)^2 \Rightarrow BH=\frac{49\sqrt{74}}{74} \approx 5.7$
Vậy độ dài cạnh huyền BC, đường cao AH, đoạn thẳng CH và BH lần lượt gần bằng 8.6; 4.1; 2.9 và 5.9 ĐVĐD
#3. Lời kết
Vâng, trên đây là các hệ thức lượng trong tam giác vuông mà bạn cần phải nắm được. Tùy theo giả thuyết của bài toán đưa ra mà chúng ta sẽ cân nhắc, lựa chọn hệ thức sao cho phù hợp nhất.
Trong thời gian đầu khi giải bài tập bạn nên vẽ hình và ghi toàn bộ các hệ thức ra giấy nháp, việc làm này có hai lợi ích:
- Giúp bạn nhanh nhớ, nhớ chính xác và nhớ lâu.
- Giúp bạn nhanh chóng chọn được hệ thức phù hợp để áp dụng vào bài tập.
Okay, hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo nhé !
Đọc thêm:
- Công thức tính DIỆN TÍCH TỨ GIÁC và CHU VI TỨ GIÁC
- Cách tính thể tích tứ diện trong không gian (công thức & casio)
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
 Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống