Tam giác Pascal là gì? Bài tập ví dụ về tam giác Pascal

Khai triển đa thức là biến đổi một đa thức ở dạng tích các tổng, hoặc hiệu thành dạng tổng, hoặc hiệu các tích.

Khai triển đa thức là một trong những kiến thức cơ bản của môn Đại số mà ngay từ những năm Trung học cơ sở chúng ta đã được học

Trong rất nhiều bài toán chúng ta cần thực hiện thao tác khai triển mới có thể tìm ra đáp án, tiêu biểu như rút gọn biểu thức, rút gọn phân thức, giải phương trình, tính giới hạn, đạo hàm, tích phân, …

Về cơ bản thì quá trình khai triển không có gì khó khăn cả, nhưng khai triển sao cho nhanh chóng và chính xác thì không phải ai cũng làm được.

Có khá nhiều cách giúp chúng ta khai triển đa thức nhanh chóng và chính xác, trong đó dựa vào tam giác Pascal là một trong những cách phổ biến nhất. Và đó cũng là nội dung chính trong bài viết này.

#1. Tam giác Pascal là gì?

Tam giác Pascal là một mảng tam giác của các hệ số nhị thức. Các con số được sắp xếp để chúng phản ánh như một hình tam giác.

Tam giác Pascal được đặt tên theo tên của nhà Toán học đã tìm ra nó (Blaise Pascal).

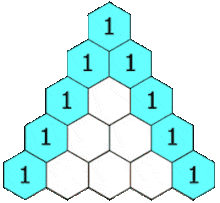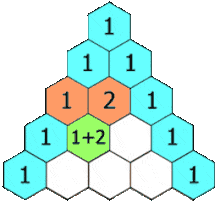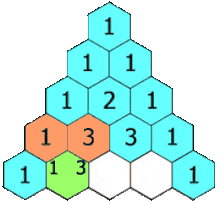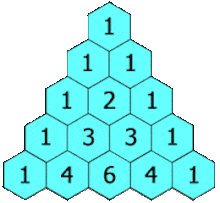
#2. Cách xây dựng tam giác Pascal

Bước 1. Dòng thứ nhất viết một con số 1

Bước 2. Dòng thứ 2, viết hai con số 1

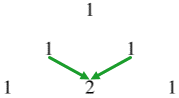
Bước 3. Dòng thứ ba …

a) Ở vị trí đầu dòng và cuối dòng viết số 1

b) Số ở chính giữa bằng tổng của hai số ở dòng thứ 2

Bước 4. Dòng thứ 4, dòng thứ 5, dòng thứ 6, …, thực hiện tương tự Bước 3

#3. Ứng dụng tam giác Pascal trong giải toán như thế nào?

Hầu hết chúng ta đều sử dụng tam giác Pascal để khai triển các nhị thức, tức là các biểu thức có dạng $(ax \pm by)^n$

Chẳng hạn như: $(x+y)^2, (x-y)^3, (2x+3y)^2, \left(\frac{2}{3}x-\frac{5}{7}y\right)^3$

Chú ý:

• n là một số tự nhiên.
• a, b có thể là số thực hoặc đa thức.

#4. Bài tập ví dụ minh họa tam giác Pascal

Ví dụ 1. Khai triển nhị thức $(x+y)^2$

Trình bày lời giải:

$(x+y)^2=+1x^2y^0+2x^1y^1+1x^0y^2=x^2+2xy+y^2$

Ví dụ 2. Khai triển nhị thức $(x-y)^3$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

• Vì dấu của nhị thức là dấu – nên dấu của các hạng tử lần lượt là +, -, +, –
• Vì n = 3 nên chúng ta sẽ sử dụng dòng thứ tư của tam giác tức 1, 3, 3, 1

Lời giải:

$(x-y)^3=+1x^3y^0-3x^2y^1+3x^1y^2-1x^0y^3=x^3+3x^2y+3xy^2+y^3$

Ví dụ 3. Khai triển nhị thức $(2x+3y)^2$

• Vì dấu của nhị thức là dấu + nên dấu của các hạng tử sẽ là +, +, +
• Vì n = 2 nên chúng ta sẽ sử dụng dòng thứ ba của tam giác tức 1, 2, 1

Lời giải:

$(2x+3y)^2=+1(2x)^2(3y)^0+2(2x)^1(3y)^1+1(2x)^0(3y)^2=4x^2+12xy+9y^2$

Ví dụ 4. Khai triển nhị thức $\left(\frac{2}{3}x-\frac{5}{7}y\right)^3$

• Vì dấu của nhị thức là dấu – nên dấu của các hạng tử lần lượt là +, -, +, –
• Vì n = 3 nên chúng ta sẽ sử dụng dòng thứ tư của tam giác tức 1, 3, 3, 1

Lời giải:

$\left(\frac{2}{3}x-\frac{5}{7}y\right)^3$

$=+1\left(\frac{2}{3}x\right)^3\left(\frac{5}{7}y\right)^0-3\left(\frac{2}{3}x\right)^2\left(\frac{5}{7}y\right)^1+3\left(\frac{2}{3}x\right)^1\left(\frac{5}{7}y\right)^2-1\left(\frac{2}{3}x\right)^0\left(\frac{5}{7}y\right)^3$

$=\frac{8}{27} x^{3}-\frac{20}{21} x^{2} y+\frac{50}{49} x y^{2}-\frac{125}{343} y^{3}$

Ví dụ 5. Khai triển đa thức $(2x+3y-5z)^2$

Nhận xét $(2x+3y-5z)^2$ không phải là một nhị thức nhưng nếu biết cách sử dụng linh hoạt chúng ta vẫn có thể dựa vào tam giác Pascal để hỗ trợ quá trình khai triển

Cách 1: Sử dụng tam giác Pascal

$(2x+3y-5z)^2=[(2x+3y)-5z]^2$

• Vì dấu của $[(2x+3y)-5z]^2$ là dấu – nên dấu của các hạng tử lần lượt là +, -, +
• Vì n = 2 nên chúng ta sẽ sử dụng dòng thứ ba của tam giác tức 1, 2, 1

Lời giải:

$[(2x+3y)-5z]^2$

$=+1(2x+3y)^2(5z)^0-2(2x+3y)^1(5z)^1+1(2x+3y)^0(5z)^2$

$=(2x+3y)^2-2(2x+3y)(5z)+25z^2$

Vì $(2x+3y)^2=4x^2+12xy+9y^2$ nên …

$=(4x^2+12xy+9y^2)-2(2x+3y)(5z)+25z^2$

$=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$

Cách 2: Sử dụng hằng đẳng thức

Để khai triển nhanh đa thức $(2x+3y-5z)^2$ bạn có thể sử dụng hằng đẳng thức $(a+b-c)^2=a^{2}+2 a b-2 a c+b^{2}-2 b c+c^{2}$

Ở đây a, b, c trong công thức sẽ lần lượt bằng 2x, 3y, 5z

$(2x+3y-5z)^2$

$=(2x)^2+2(2x)(3y)-2(2x)(5z)+(3y)^2-2(3y)(5z)+(5z)^2$

$=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$

Cách 3: Nhân đa thức với đa thức

Cách này rất tốn thời gian nên mình không khuyến khích sử dụng, chỉ sử dụng khi bạn quên mất cách lập tam giác Pascal và quên luôn hằng đẳng thức $(a+b-c)^2$

$(2x+3y-5z)^2$

$=(2x+3y-5z)(2x+3y-5z)$

$=2x.2x+2x.3y-2x.5z+3y.2x+3y.3y-3y.5z-5z.2x-5z.3y+5z.5z$

$=4 x^{2}+12 x y-20 x z+9 y^{2}-30 y z+25 z^{2}$

#5. Lời kết

Như vậy tam giác Pascal sẽ giúp chúng ta khai triển nhanh các biểu thức có dạng $(ax \pm by)^2$ hoặc các biểu thức có dạng gần gần như vậy.

Tương tự như các phương pháp khác, phương pháp này cũng có một số nhược điểm nhất định, đó là:

• Giả sử bạn cần sử dụng kết quả của dòng thứ 6 thì bạn phải bắt đầu lập từ dòng thứ 1 chứ không thể bắt đầu từ dòng thứ 5 từ khi bạn thuộc được dòng thứ 5.
• Khi n có giá trị lớn hơn 10 thì việc khai triển bằng cách dựa vào tam giác Pascal khá tốn thời gian.

Để khắc phục 2 nhược điểm trên bạn có thể tìm hiểu về thêm nhị thức Newton trên Wikipedia nhé. Hi vọng bài viết này sẽ hữu ích với bạn, xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• 7 cách giải phương trình bậc hai đơn giản, hiệu quả
• Tính khoảng cách giữa 2 đường thẳng chéo nhau bằng CASIO

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com