Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Mục Lục Nội Dung
I. Tứ giác đặc biệt là gì?
Tứ giác đặc biệt là một tứ giác lồi và có thêm các yếu tố đặc biệt về độ dài của cạnh, độ lớn của góc, quan hệ giữa các cạnh, quan hệ giữa các góc, …
Chẳng hạn như có một cặp cạnh song song, các cạnh đối song song từng đôi một, các góc bằng nhau, …
Trên thực tế có khá nhiều tứ giác đặc biệt, nhưng ở đây mình chỉ trình bày với các bạn định nghĩa, tính chất và dấu hiệu nhận biết của năm loại tứ giác đặc biệt thường gặp nhất: là hình thang, hình bình hành, hình chữ nhật, hình thôi và hình vuông.
#1. Hình thang
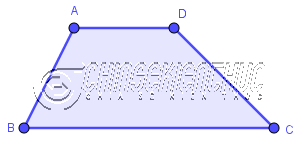
Tứ giác lồi có một cặp cạnh song song thì được gọi là hình thang.
Tứ giác lồi ABCD có AD song song với BC => nên tứ giác này là một hình thang.
Trong một hình thang bất kì ta luôn có …
- Hai góc kề cùng một cạnh bên thì bù nhau hay có tổng số đo bằng 1800
- Đường trung bình song song với hai đáy và có độ dài bằng độ dài nửa tổng độ dài hai đáy
Muốn chứng minh một tứ giác lồi là một hình thang chúng ta cần chứng minh được một trong hai ý.
- Có một cặp cạnh song song
- Có hai góc kề với một cạnh bù nhau
#2. Hình bình hành
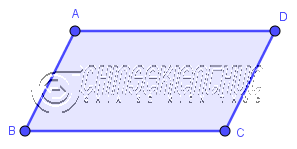
Tứ giác lồi có hai cặp cạnh đối song song từng đôi một thì được gọi là hình bình hành.
Tứ giác lồi ABCD có AB song song DC, AD song song BC nên tứ giác này là một hình bình hành
Trong một hình bình hành bất kì ta luôn có …
- Các cặp cạnh đối bằng nhau từng đôi một*
- Các góc kề với mỗi cạnh bù nhau*
- Các góc đối bằng nhau từng đôi một*
- Hai đường chéo cắt nhau tại trung điểm mỗi đường*
- Một tâm đối xứng
Muốn chứng minh một tứ giác lồi là một hình bình hành chúng ta cần chứng minh được một trong ba ý
- Là một hình chữ nhật
- Có một trong bốn tính chất*
- Có một cặp cạnh đối diện song song và bằng nhau
#3. Hình chữ nhật
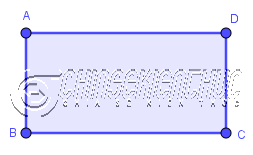
Hình bình hành có tất cả các góc bằng nhau thì được gọi là hình chữ nhật
Hình bình hành ABCD có $\hat{A}=\hat{B}=\hat{C}=\hat{D}$ => nên hình bình hành này là một hình chữ nhật.
Trong một hình chữ nhật bất kì ta luôn có …
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm (điểm chính giữa) của mỗi đường
- Bốn góc vuông
- Hai trục đối xưng (đường trung trực của mỗi cặp cạnh)
- Một tâm đối xứng (giao điểm của hai đường chéo)
Muốn chứng minh một tứ giác lồi là một hình chữ nhật chúng ta cần chứng minh được một trong hai ý:
- Thỏa mãn định nghĩa
- Có ba góc vuông
Muốn chứng minh một hình bình hành là một hình chữ nhật chúng ta cần chứng minh được một trong hai ý:
- Có một góc vuông
- Có hai đường chéo bằng nhau
#4. Hình thoi
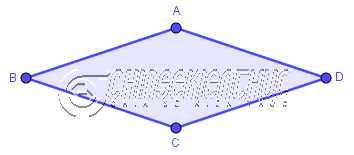
Hình bình hành có tất cả các cạnh bằng nhau được gọi là hình thoi.
Hình bình hành ABCD có $AB=BC=CD=DA$ nên hình bình hành này là một hình thôi
Trong một hình thôi bất kì ta luôn có …
- Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm mỗi đường
- Hai đường chéo cũng là hai đường phân giác
- Một tâm đối xứng
Muốn chứng minh một tứ giác lồi là một hình thoi chúng ta cần chứng minh được một trong hai ý:
- Thỏa mãn định nghĩa
- Có bốn cạnh bằng nhau
Muốn chứng minh một hình bình hành là một hình thoi chúng ta cần chứng minh được một trong ba ý:
- Có hai cạnh liên tiếp bằng nhau
- Có hai đường chéo vuông góc với nhau
- Có một đường chéo đồng thời là đường phân giác của một góc
#5. Hình vuông
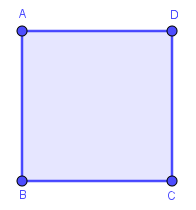
Hình bình hành có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau được gọi là hình vuông.
Hình bình hành ABCD có $AB=BC=CD=DA$ và có $\hat{A}=\hat{B}=\hat{C}=\hat{D}$ nên hình bình hành này là một hình vuông
Trong một hình vuông bất kì ta luôn có …
- Bốn góc vuông
- Bốn cạnh bằng nhau
- Hai đường chéo vuông góc với nhau và bằng nhau
- Hai đường chéo cũng là đường phân giác của các góc
- Hai trục đối xứng
- Một tâm đối xứng
Muốn chứng minh một hình chữ nhật là một hình vuông chúng ta cần chứng minh được một trong hai ý
- Có hai cạnh liên tiếp bằng nhau
- Có hai đường chéo vuông góc với nhau
Muốn chứng minh một hình thoi là một hình chữ nhật chúng ta cần chứng minh được nó có một góc vuông
II. Lời kết
Như vậy là mình đã giới thiệu cho các bạn đầy đủ về định nghĩa, tính chất, cũng như dấu hiệu nhận biết (cách chứng minh) của năm loại tứ giác thường gặp nhất rồi nhé.
Như các bạn có thể thấy, trong ba mạch kiến thức trên thì mạch kiến thức về dấu hiệu nhận biết là rắc rối nhất..
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
Chẳng hạn để chứng minh tứ giác đã cho là hình chữ nhật, trong nhiều trường hợp ta không thể chứng minh trực tiếp bằng định nghĩa mà phải chứng minh gián tiếp thông qua một tứ giác nào đó, …
Vậy nên là bạn cần đọc kỹ, nghiền ngẫm và áp dụng vào giải bài tập thì mới có thể nhớ chính xác được. Hi vọng bài viết này sẽ hữu ích với bạn ,xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo ha !
Đọc thêm:
- 11 loại góc thường gặp trong hình học nhất định phải biết
- Cách tính Chu vi và Diện tích của hình thang (có ví dụ dễ hiểu)
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
