Blog Chia Sẻ Kiến Thức Máy tính – Công nghệ & Cuộc sống
Để nắm bắt được chính xác và nhanh chóng các thông tin quan trọng của mẫu số liệu mà các nhà Toán học đã nghiên cứu và đề xuất các giá trị được gọi là các số đặc trưng
Các số đặc trưng thường gặp là trung bình cộng, tứ phân vị, phương sai, độ lệch chuẩn. Trong đó:
- Trung bình cộng, tứ phân vị được gọi là số đặc trưng đo xu thế trung tâm.
- Phương sai, độ lệch chuẩn được gọi là số đặc trưng độ phân tán.
Vâng, hôm nay chúng ta sẽ cùng nhau tìm hiểu về ý nghĩa của số phương sai, độ lệch chuẩn nha các bạn.
Mục Lục Nội Dung
#1. Khoảng biến thiên và khoảng tứ phân vị
Khoảng biến thiên đặc trưng cho độ phân tán của toàn bộ mẫu số liệu.
Khoảng tứ phân vị đặc trưng cho độ phân tán của một nữa các số liệu và có giá trị thuộc đoạn từ $Q_1$ đến $Q_3$ trong mẫu.
Khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị rất lớn hoặc rất bé trong mẫu.
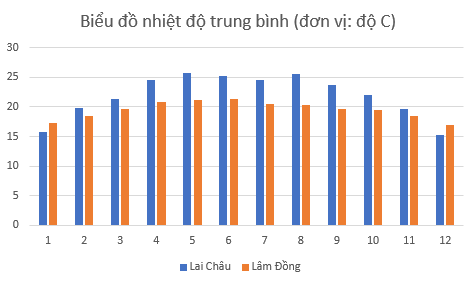
Ví dụ 1. Cho Biểu đồ nhiệt độ trung bình (đơn vị: oC) các tháng trong năm 2020 của hai tỉnh Lai Châu và Lâm Đồng.
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Lai Châu | 15.8 | 19.8 | 21.3 | 24.5 | 25.7 | 25.2 | 24.6 | 25.6 | 23.7 | 22 | 19.6 | 15.2 |
| Lâm Đồng | 17.3 | 18.4 | 19.7 | 20.8 | 21.2 | 21.3 | 20.5 | 20.3 | 19.6 | 19.5 | 18.5 | 17 |
- a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.
- b) Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ôn hòa hôn.
Lời giải:
a)
+) Lai Châu
Xét mẫu số liệu đã sắp xếp là:
| 15.2 | 15.8 | 19.6 | 19.8 | 21.3 | 22 | 23.7 | 24.5 | 24.6 | 25.2 | 25.6 | 25.7 |
Khoảng biến thiên của mẫu số liệu là $R=25.7-15.2=10.5$
Cỡ mẫu là $n=12$ là số chẵn nên giá trị tứ phân vị thứ hai là $Q_2=\frac{22+23.7}{2}=22.85$
Tứ phân vị thứ nhất là trung vị của mẫu:
| 15.2 | 15.8 | 19.6 | 19.8 | 21.3 | 22 |
=> $Q_1=\frac{19.6+19.8}{2}=19.7$
Tứ phân vị thứ ba là trung vị của mẫu:
| 23.7 | 24.5 | 24.6 | 25.2 | 25.6 | 25.7 |
=> $Q_3=\frac{24.6+25.2}{2}=24.9$
Khoảng tứ phân vị của mẫu là $\Delta_Q=24.9-19.7=5.2$
+) Lâm Đồng
Xét mẫu số liệu đã sắp xếp là:
 |
 |
| Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki] |
CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada] |
| 17 | 17.3 | 18.4 | 18.5 | 19.5 | 19.6 | 19.7 | 20.3 | 20.5 | 20.8 | 21.2 | 21.3 |
Khoảng biến thiên của mẫu số liệu là $R=21.3-17=4.3$
Cỡ mẫu là $n=12$ là số chẵn nên giá trị tứ phân vị thứ hai là $Q_2=\frac{19.6+19.7}{2}=19.65$
Tứ phân vị thứ nhất là trung vị của mẫu:
| 17 | 17.3 | 18.4 | 18.5 | 19.5 | 19.6 |
=> $Q_1=\frac{18.4+18.5}{2}=18.45$
Tứ phân vị thứ ba là trung vị của mẫu:
| 19.7 | 20.3 | 20.5 | 20.8 | 21.2 | 21.3 |
Suy ra $Q_3=\frac{20.5+20.8}{2}=20.65$
Khoảng tứ phân vị của mẫu là $\Delta_Q=20.65-18.45=2.2$
b) Trong một năm nhiệt độ của Lâm Đồng ôn hòa hơn (ít thay đổi hơn) của Lai Châu
#2. Phương sai và độ lệch chuẩn
Phương sai là trung bình cộng của các bình phương độ lệch từ mỗi giá trị của mẫu số liệu đến số trung bình.
Phương sai và độ lệch chuẩn được dùng để đo mức độ phân tán của các số liệu trong mẫu quanh số trung bình.
Phương sai và độ lệch chuẩn càng lớn thì các giá trị của mẫu càng cách xa nhau tức có độ phân tán lớn.
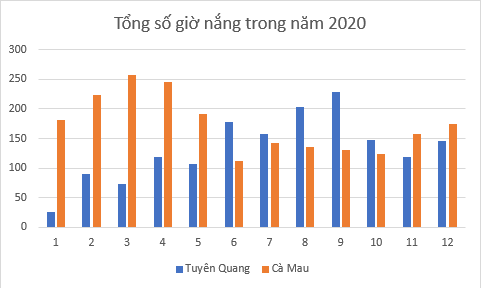
Ví dụ 2. Bảng dưới đây thống kê tổng số giờ nắng trong năm 2020 theo từng tháng được đo bởi hai trạm quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Tuyên Quang | 26 | 90 | 73 | 118 | 107 | 178 | 157 | 204 | 228 | 147 | 118 | 146 |
| Cà Mau | 181 | 224 | 258 | 246 | 192 | 112 | 142 | 135 | 131 | 123 | 158 | 174 |
- a) Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh
- b) Nêu nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh
Lời giải:
a)
Các bạn sử dụng công thức (cách tính các số đặc trưng) hoặc máy tính cầm tay Casio để tính các bạn nhé.
Ở đây mình sẽ hướng dẫn tính bằng ứng dụng Excel:
Bước 1. Nhập bảng thống kê:
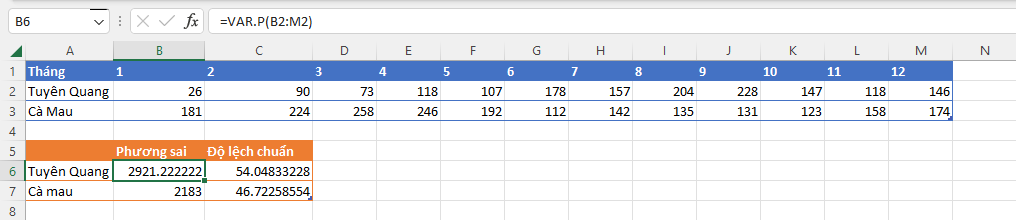
Bước 2. Sử dụng hàm =VAR.P() để tính phương sai.
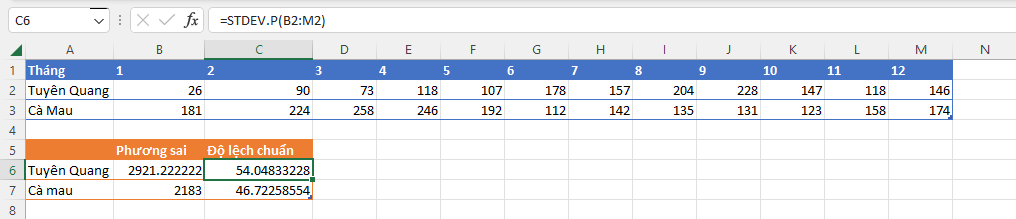
Bước 3. Sử dụng hàm =STDEV.P() để tính độ lệch chuẩn
b)
Vì phương sai và độ lệch chuẩn tổng số giờ nắng ở Tuyên Quang lớn hơn phương sai và độ lệch chuẩn tổng số giờ nắng ở Cà Mau.
Vậy nên, tổng số giờ nắng ở Tuyên Quang theo từng tháng có sự biến động lớn hơn ở Cà Mau.
#3. Lời kết
Thống kê giúp chúng ta phân tích được mẫu số liệu và rút ra được nhiều thông tin hữu ích một cách chính xác.
Muốn thực hiện được các công việc trên thì ngoài việc phải hiểu ý nghĩa của các số đặc trưng (phương sai, độ lệch chuẩn…) ra, chúng ta còn phải biết cách trình bày mẫu số liệu và cách tính các số đặc trưng nữa.
- Mẫu số liệu thường được trình bày dưới dạng bảng thông thường, bảng phân bố tần số, dạng bảng tần số ghép lớp.
- Công thức tính các số đặc trưng đã được mình tổng hợp đầy đủ trong bài viết này.
Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !
CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn
