3 cách chứng minh hai tam giác bằng nhau (có ví dụ dễ hiểu)

Ở trong những bài viết trước thì chúng ta đã cùng nhau tìm hiểu về hai đoạn thẳng bằng nhau, hai góc bằng nhau, … rồi phải không nào.

Và để tiếp tục mạch kiến thức này thì hôm nay chúng ta sẽ cùng nhau tìm hiểu về ba trường hợp bằng nhau của hai tam giác.

Việc chứng minh hai tam giác bằng nhau có nhiều ứng dụng trong Toán học, tiêu biểu nhất là có thể gián tiếp chứng minh được các cạnh, các góc tương ứng bằng nhau.

I. Hai tam giác bằng nhau là hai tam giác như thế nào?

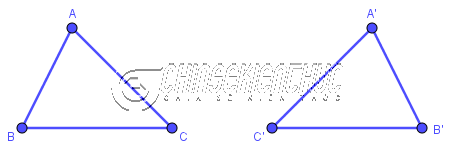
Nếu tam giác này có ba cạnh và ba góc lần lượt bằng ba cạnh và ba góc của tam giác kia thì hai tam giác đã cho bằng nhau.

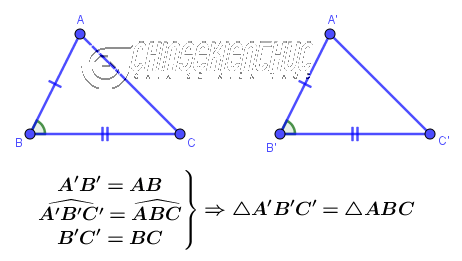
Vì $AB=A’B’, BC=B’C’, CA=C’A’$ và $\hat{A}=\hat{A’}, \hat{B}=\hat{B’}, \hat{C}=\hat{C’}$ nên $\triangle ABC=\triangle A’B’C’$

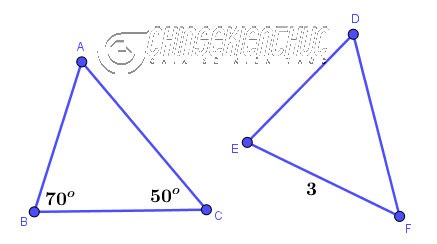
Ví dụ 1: Cho $\triangle ABC = \triangle DEF$ có $\hat{B}=70^o, \hat{C}=50^o, EF=3$. Tính số đo của $\hat{D}$ và độ dài của cạnh $BC$

Lời Giải:

$\hat{A}+\hat{B}+\hat{C}=180$ (theo Định lý Tổng ba góc trong một tam giác)

$\Leftrightarrow \hat{A}+70^o+50^o=180^o$

$\Leftrightarrow \hat{A}+120^o=180^o$

Suy ra $\hat{A}=180^o-120^o=60^o$

Vì $\triangle ABC = \triangle DEF$ nên các cạnh, cách góc tương ứng bằng nhau

• $\hat{A}=\hat{D}=60^o$
• $BC=EF=3$

Vậy số đo của $\hat{D}=60$ và độ dài của cạnh $BC=3$

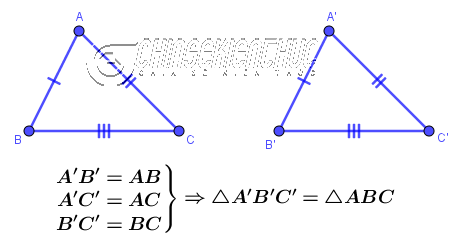
#1. Chứng minh 2 tam giác bằng nhau (Cạnh – Cạnh – Cạnh)

Nếu ba cạnh của tam giác này lần lượt bằng ba cạnh của tam giác kia thì hai tam giác đã cho bằng nhau.

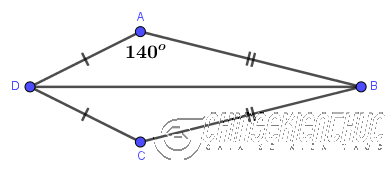
Ví dụ 2: Cho tứ giác ABCD có $AD=CD, AB=CB, \hat{A}=140^o$. Tính số đo $\hat{C}$

Lời Giải:

Xét $\triangle ABD = \triangle CBD$

• $AD=CD$
• $AB=CB$
• DC là cạnh chung

Suy ra $\triangle ABD = \triangle CBD$ (Cạnh – Cạnh – Cạnh)

Suy ra $\hat{A}=\widehat{C}=140^o$

Vậy số đo $\hat{C}=140^o$

#2. Chứng minh 2 tam giác bằng nhau (Cạnh – Góc – Cạnh)

Nếu hai cạnh và góc xen giữa của tam giác này lần lượt bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đã cho bằng nhau.

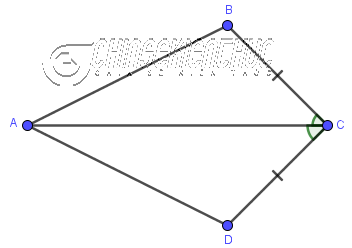
Ví dụ 3: Cho tứ giác ABCD có $BC=DC, \widehat{BCA}=\widehat{DCB}$. Chứng minh $\triangle ABC = \triangle ADC$

Lời Giải:

Xét $\triangle ABC$ và $\triangle ADC$

• $BC=DC$
• $\widehat{BCA}=\widehat{DCA}$
• $AC$ cạnh chung

Vậy $\triangle ABC = \triangle ADC$ (Cạnh – Góc – Cạnh)

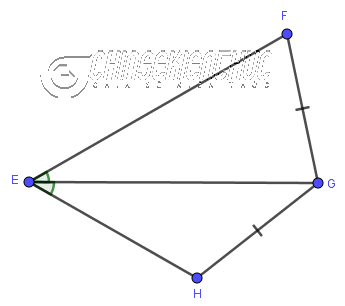
Ví dụ 4: Cho tứ giác $EFGH$ có $FG=HG, \widehat{FEG}=\widehat{HEG}$. Tam giác FEG có bằng tam giác HEG không? Vì sao?

Lời Giải:

Câu trả lời là: Không bằng nhau!

Tuy $\widehat{FEG}=\widehat{HEG}$ nhưng …

• $\widehat{FEG}$ không phải là góc xen giữa FG và EG
• $\widehat{HEG}$ cũng không phải là góc xen giữa HG và EG

Giả sử chúng ta có $EF=EH$ hoặc $\widehat{FGE}=\widehat{HGE}$ thì lúc bấy giờ tam giác FEG sẽ bằng tam giác HEG (Cạnh – Góc – Cạnh)

#3. Chứng minh 2 tam giác bằng nhau (Góc – Cạnh – Góc)

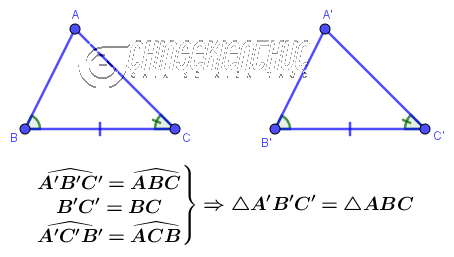
Nếu một cạnh và hai góc kề của tam giác này lần lượt bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đã cho bằng nhau.

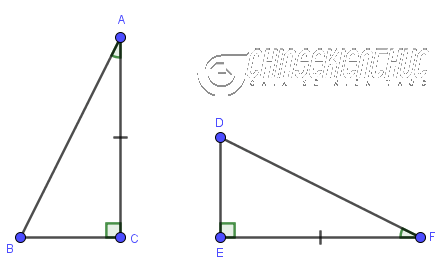
Ví dụ 5: Tam giác ABC có bằng tam giác DEF hay không? Vì sao?

Lời Giải:

Tam giác ABC bằng tam giác DEF

Vì …

• $\hat{A}=\hat{F}$
• $AC=FE$
• $\hat{C}=\hat{E}$

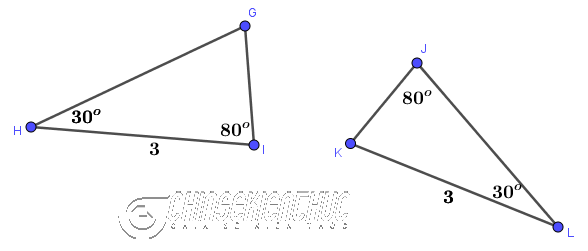
Ví dụ 6: Tam giác GHI có bằng tam giác JKL hay không? Vì sao?

Lời Giải:

Câu trả lời: Hai tam giác trên không bằng nhau.

Vì …

• HI có hai góc kề là $\hat{H}=30^o$ và $\hat{I}=80^o$
• KL có hai góc kề là $\hat{K}=180^o-(\hat{J}+\hat{L})=180-(80+30)=70^o$ và $\hat{L}=30^o$

Giả sử $\hat{I}=70^o$ hoặc $\hat{J}=70^o$ thì lúc bấy giờ tam giác GHI sẽ bằng tam giác JKL (Góc – Cạnh – Góc)

II. Lời kết

Vâng, trên đây là 3 cách để chứng minh 2 tam giác bằng nhau, đây là những cách chứng minh đơn giản và được sử dụng nhiều nhất trong hình học.

Hai tam giác bằng nhau thì sẽ có ba cạnh tương ứng bằng nhau, ba góc tương ứng bằng nhau, diện tích bằng nhau, …

Tuy nhiên điều ngược lại trong nhiều trường hợp có thể không đúng, thật vậy hai tam giác có ba góc bằng nhau có thể không bằng nhau, …

Ngoài ra, các bạn cần chú ý khi chứng minh theo trường hợp thứ 2 và thứ 3 thì góc phải là góc xen giữa, cạnh phải là cạnh xen giữa nha các bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Định lý Pytago thuận, định lý Pytago đảo và bài tập ví dụ !
• 11 loại góc thường gặp trong hình học nhất định phải biết

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com