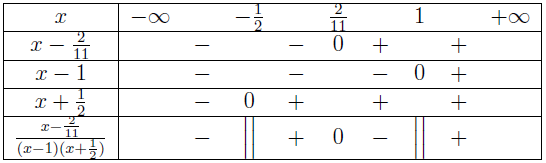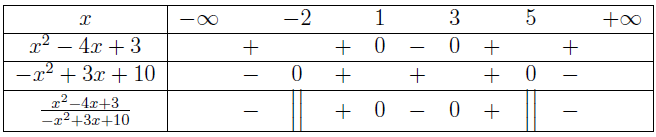Cách giải bất phương trình chứa ẩn ở mẫu (có bài ví dụ)

Hôm nay, chúng ta sẽ cùng nhau tìm hiểu về cách giải các bất phương trình có thể biến đổi sơ cấp đưa về dạng:

$\frac{P(x)}{Q(x)}<0$ hoặc $\frac{P(x)}{Q(x)} \leq 0$ hoặc $\frac{P(x)}{Q(x)} \geq 0$ hoặc $\frac{P(x)}{Q(x)}>0$

Với $P(x)$, $Q(x)$ là tích của những nhị thức bậc nhất hoặc tam thức bậc hai.

Các bất phương trình có dạng vừa trình bày được gọi chung là bất phương trình chứa ẩn ở mẫu.

#1. Cách giải bất phương trình chứa ẩn ở mẫu

Để giải các bất phương trình chứa ẩn ở mẫu có dạng (hoặc có thể biến đổi để đưa về dạng):

$\frac{P(x)}{Q(x)}<0$ hoặc $\frac{P(x)}{Q(x)} \leq 0$ hoặc $\frac{P(x)}{Q(x)} \geq 0$ hoặc $\frac{P(x)}{Q(x)}>0$

… thì chúng ta thường lập bảng xét dấu phân thức $\frac{P(x)}{Q(x)}$

Trong quá trình lập bảng xét dấu cần phải:

• Ghi tất cả các nghiệm của hai đa thức $P(x)$ và $Q(x)$ lên trục số.
• Dòng cuối cùng tại những điểm mà $Q(x)=0$ chúng ta sử dụng ký hiệu $||$ để chỉ tại đó bất phương trình đã cho không xác định.

#2. Bài tập giải bất phương trình chứa ẩn ở mẫu

Ví dụ 1. Giải bất phương trình $\frac{2}{3x+5}>\frac{7}{11x+13}$

Mặc dù bất phương trình $\frac{2}{3x+5}>\frac{7}{11x+13}$ không có dạng $\frac{P(x)}{Q(x)}>0$ nhưng chúng ta hoàn toàn có thể biến đổi sơ cấp đưa về dạng $\frac{P(x)}{Q(x)}>0$ một cách dễ dàng.

Lời giải:

$\frac{2}{3x+5}>\frac{7}{11x+13}$

$\Leftrightarrow \frac{2}{3x+5}-\frac{7}{11x+13}>0$

$\Leftrightarrow \frac{2(11x+13)}{(3x+5)(11x+13)}-\frac{7(3x+5)}{(11x+13)(3x+5)}>0$

$\Leftrightarrow \frac{2(11x+13)-7(3x+5)}{(3x+5)(11x+13)}>0$

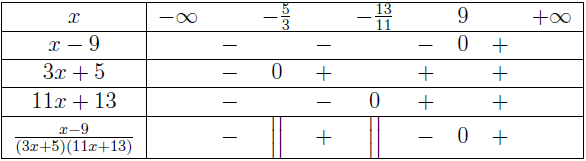
$\Leftrightarrow \frac{x-9}{(3x+5)(11x+13)}>0$

Đặt $\frac{P(x)}{Q(x)}=\frac{x-9}{(3x+5)(11x+13)}$

Dễ thấy, tử thức $x-9$ có một nghiệm đơn là $9$

Dễ thấy, mẫu thức $(3x+5)(11x+13)$ có hai nghiệm đơn là $-\frac{5}{3}$ và $-\frac{13}{11}$

Bảng xét dấu $\frac{P(x)}{Q(x)}$

Vì dấu của bất phương trình là dấu lớn nên những khoảng dương trên bảng xét dấu chính là nghiệm của bất phương trình

Vậy => tập nghiệm của bất phương trình đã cho là $\left(-\frac{5}{3}, -\frac{13}{11}\right) \cup (9, +\infty)$

Ví dụ 2. Giải bất phương trình $\frac{2x^2+3x-5}{x^2+2x-3} \geq 0$

Lời giải:

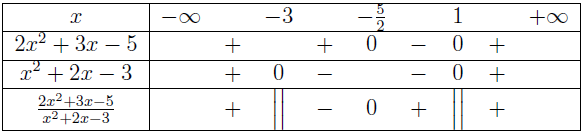
Đặt $\frac{P(x)}{Q(x)}=\frac{2x^2+3x-5}{x^2+2x-3}$

Dễ thấy, tử thức $2x^2+3x-5$ có hai nghiệm đơn là $1$ và $-\frac{5}{2}$

Dễ thấy, mẫu thức $x^2+2x-3$ có hai nghiệm đơn là $1$ và $-3$

Bảng xét dấu $\frac{P(x)}{Q(x)}$

Vì dấu của bất phương trình là dấu lớn hoặc bằng nên những khoảng dương và những mút không là nghiệm của mẫu thức trên bảng xét dấu chính là nghiệm của bất phương trình

Vậy => tập nghiệm của bất phương trình đã cho là $(-\infty, -3) \cup \left[-\frac{5}{2} , 1\right) \cup (1, +\infty)$

#3. Bài tập tự luyện

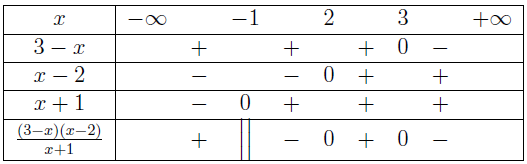
Bài tập 1. Giải bất phương trình $\frac{(3-x)(x-2)}{x+1} \leq 0$

Hướng dẫn:

Bảng xét dấu $\frac{(3-x)(x-2)}{x+1}$

Tập nghiệm của bất phương trình đã cho là $(-1,2] \cup [3, +\infty)$

Bài tập 2. Giải bất phương trình $\frac{3}{1-x} \geq \frac{5}{2 x+1}$

Hướng dẫn:

Bất phương trình đã cho tương đương với $\frac{x-\frac{2}{11}}{(x-1)\left(x+\frac{1}{2}\right)} \leq 0$

Bảng xét dấu $\frac{x-\frac{2}{11}}{(x-1)\left(x+\frac{1}{2}\right)}$

Tập nghiệm của bất phương trình đã cho là $\left(-\infty,-\frac{1}{2}\right) \cup \left[\frac{2}{11}, 1\right)$

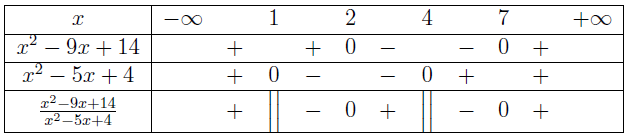
Bài tập 3. Giải bất phương trình $\frac{x^2-9 x+14}{x^2-5 x+4}>0$

Hướng dẫn:

Bảng xét dấu $\frac{x^2-9 x+14}{x^2-5 x+4}$

Tập nghiệm của bất phương trình đã cho là $(-\infty, 1) \cup (2,4) \cup (7, +\infty)$

Bài tập 4. Giải bất phương trình $\frac{-2 x^2+7 x+7}{x^2-3 x-10} \leq-1$

Hướng dẫn:

Bất phương trình đã cho tương đương với $\frac{x^2-4 x+3}{-x^2+3 x+10} \leq 0$

Bảng xét dấu $\frac{x^2-4 x+3}{-x^2+3 x+10}$

Tập nghiệm của bất phương trình đã cho là $(-\infty,-2) \cup [1,3] \cup (5, +\infty)$

Xem thêm:
Cách lập bảng xét dấu tự động bằng phần mềm Geophar

#4. Lời kết

Vâng, trên đây là cách giải bất phương trình chứa ẩn ở mẫu mà mình muốn chia sẻ đến các bạn.

Nếu  tử thức và mẫu thức là những đa thức bậc ba, bậc bốn, bậc năm, … thì trước hết bạn hãy cố gắng phân tích nó thành tích của những nhị thức bậc nhất hoặc tam thức bậc hai.

Chắc chắn có thể phân tích được (các nhà Toán học đã được chứng minh nhận định này) vấn đề là dễ hay khó, nhanh hay chậm mà thôi.

Sau khi phân tích hãy áp dụng theo những chỉ dẫn vừa trình bày và các kiến thức về dấu nhị thức bậc nhất, dấu tam thức bậc hai

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn