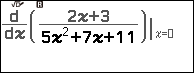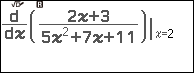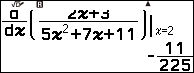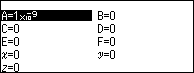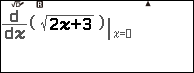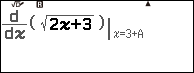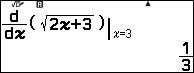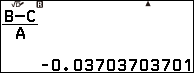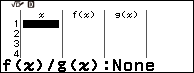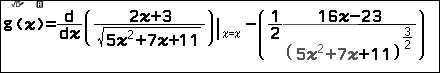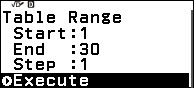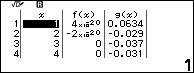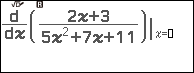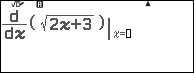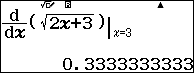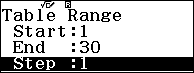Cách tính đạo hàm bằng máy CASIO 580 VNX và 880 BTG

Trong bài viết này mình sẽ hướng dẫn cho các bạn sử dụng máy tính CASIO để tính đạo hàm cấp một tại một điểm, cấp hai tại một điểm và cấp một với bốn phương án cho trước.

Việc tính đạo hàm bằng máy tính CASIO có nhiều giá trị trong học tập, kiểm tra và thi cử.

Chẳng hạn xác định nghiệm của đa thức bậc ba là nghiệm đơn hay nghiệm kép, xác định nghiệm của đa thức bậc bốn là nghiệm bội mấy, xác định cực trị của hàm số, …

#1. Cách tính đạo hàm trên Casio fx 880 BTG

Ví dụ 1. Tính đạo hàm cấp một của hàm số $y=\frac{2x+3}{5x^2+7x+11}$ tại x=2

Bước 1. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

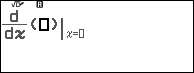
Bước 2. Nhập hàm số dưới dấu đạo hàm $y=\frac{2x+3}{5x^2+7x+11}$

Bước 3. Nhấn phím  => nhấn phím  => nhập 2

Bước 4. Nhấn phím EXE

Vậy đạo hàm cấp một của hàm số đã cho tại điểm x=2 là $-\frac{11}{225}$

Ví dụ 2. Tính đạo hàm cấp hai của hàm số $y=\sqrt{2x+3}$ tại x=3

Bước 1. Nhấn phím VARIABLE => chọn biến nhớ A => nhập $10^{-9}$ => nhấn phím OK => nhấn phím AC

Bước 2.

Bước 2.1. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

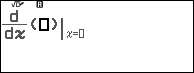
Bước 2.2. Nhập hàm số dưới dấu đạo hàm $y=\sqrt{2x+3}$

Bước 2.3. Nhấn phím  => nhấn phím  => nhập 3+A

Bước 2.4. Nhấn phím EXE

Bước 3. Nhấn phím VARIABLE => chọn biến nhớ B => nhấn phím OK => chọn Store => nhấn phím OK

Bước 4.

Bước 4.1. Nhấn phím CATALOG => chọn Func Analysis => nhấn phím OK => chọn Derivative => nhấn phím OK

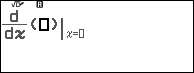
Bước 4.2. Nhập hàm số dưới dấu đạo hàm $y=\sqrt{2x+3}$

Bước 4.3. Nhấn phím  => nhấn phím  => nhập 3

Bước 4.4. Nhấn phím EXE

Bước 5. Nhấn phím VARIABLE => chọn biến nhớ C => nhấn phím OK => chọn Store => nhấn phím OK

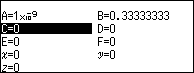
Bước 6. Nhập $\frac{B-C}{A}$ => nhấn phím EXE

 

Vậy đạo hàm cấp hai của hàm số đã cho tại x=3 gần bằng -0.03703703701

Ví dụ 3. Đạo hàm của hàm số $y=\frac{2x+3}{\sqrt{5x^2+7x+11}}$ là …

A. $-\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

B. $\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

C. $-\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

D. $\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

Bước 1. Nhấn phím HOME => chọn Table => nhấn phím OK

Bước 2. Nhấn phím TOOLS => chọn Table Type => nhấn phím OK => chọn f(x) / g(x) => nhấn phím OK => nhấn phím AC

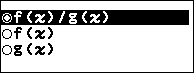
Chú ý.
Bước 2 không cần thực hiện nếu bảng giá trị Table của bạn đã có sẵn hai hàm f(x) và g(x)

Bước 3.

Bước 3.1. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK

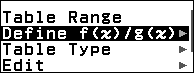
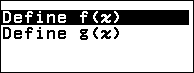
Bước 3.2. Nhập $\frac{d}{dx}\left(\frac{2x+3}{\sqrt{5x^2+7x+11}}\right)|_{x=x}-\left(-\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}\right)$

Chú ý. $-\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$ là hàm số của phương án A

Bước 3.3. Nhấn phím EXE

Bước 4.

Bước 4.1. Nhấn phím TOOLS => chọn Define f(x) / g(x) => nhấn phím OK => chọn Define f(x) => nhấn phím OK

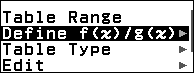
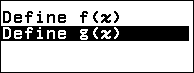
Bước 4.2. Nhập $\frac{d}{dx}\left(\frac{2x+3}{\sqrt{5x^2+7x+11}}\right)|_{x=x}-\left(\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}\right)$

Chú ý. $\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$ là hàm số của phương án B

Bước 4.3. Nhấn phím EXE

Bước 5. Nhấn phím TOOLS => chọn Table Range => nhấn phím OK => nhập 1=> nhấn phím EXE => nhập 30 => nhấn phím EXE => nhập 1 => nhấn phím EXE

Bước 6. Nhấn phím EXE

Quan sát bảng giá trị vừa tạo, hàm nào cho giá trị bằng không hoặc gần bằng không thì phương án tương ứng chính là đáp án cần tìm.

Dễ thấy phương án A là đáp án của bài toán đã cho.

#2. Cách tính đạo hàm trên Casio fx 580 VN X

Ví dụ 1. Tính đạo hàm cấp một của hàm số $y=\frac{2x+3}{5x^2+7x+11}$ tại x=2

Bước 1. Nhấn phím SHIFT => nhấn phím

Bước 2. Nhập hàm số dưới dấu đạo hàm $y=\frac{2x+3}{5x^2+7x+11}$

Bước 3. Nhấn phím  => nhấn phím  => nhập 2

Bước 4. Nhấn phím =

Vậy đạo hàm cấp một của hàm số đã cho tại x=2 là $-\frac{11}{225}$

Ví dụ 2. Tính đạo hàm cấp hai của hàm số $y=\sqrt{2x+3}$ tại x=3

Bước 1. Nhập $10^{-9}$ => nhấn phím STO => nhấn phím (-)

Bước 2.

Bước 2.1. Nhấn phím SHIFT => nhấn phím

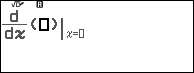
Bước 2.2. Nhập hàm số dưới dấu đạo hàm $y=\sqrt{2x+3}$

Bước 2.3. Nhấn phím  => nhấn phím  => nhập 3+A

Bước 2.4. Nhấn phím =

Bước 3. Nhấn phím STO => nhấn phím

Bước 4.

Bước 4.1. Nhấn phím SHIFT => nhấn phím

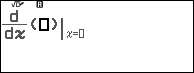
Bước 4.2. Nhập hàm số dưới dấu đạo hàm $y=\sqrt{2x+3}$

Bước 4.3. Nhấn phím  => nhấn phím  => nhập 3

Bước 4.4. Nhấn phím =

Bước 5. Nhấn phím STO => nhấn phím

Bước 6. Nhập $\frac{B-C}{A}$ => nhấn phím =

Vậy đạo hàm cấp hai của hàm số đã cho tại x=3 gần bằng -0.038434

Ví dụ 3. Đạo hàm của hàm số $y=\frac{2x+3}{\sqrt{5x^2+7x+11}}$ là …

A. $-\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

B. $\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

C. $-\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

D. $\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}$

Bước 1. Nhấn phím SHIFT => nhấn phím MENU => nhấn phím => nhấn phím => nhấn phím 1 => nhấn phím 2

Bước 2. Nhấn phím MENU => chọn Table => nhấn phím =

Bước 3.

Bước 3.1 Nhập $\frac{d}{dx}\left(\frac{2x+3}{\sqrt{5x^2+7x+11}}\right)|_{x=x}-\left(-\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}\right)$

Bước 3.2. Nhấn phím =

Bước 4.

Bước 4.1. Nhập $\frac{d}{dx}\left(\frac{2x+3}{\sqrt{5x^2+7x+11}}\right)|_{x=x}-\left(\frac{1}{2}\frac{16x-23}{(5x^2+7x+11)^{\frac{3}{2}}}\right)$

Bước 4.2. Nhấn phím =

Bước 5. Nhập 1 => nhấn phím = => nhập 30 => nhấn phím = => nhập 1 => nhấn phím =

Bước 6. Nhấn phím =

Quan sát bảng giá trị vừa tạo, hàm nào cho giá trị bằng không hoặc gần bằng không thì phương án tương ứng chính là đáp án cần tìm.

Dễ thấy phương án A là đáp án của bài toán đã cho.

#3. Lời kết

Vâng, trên đây là chi tiết các bước sử dụng máy tính CASIO tính nhanh đạo hàm cấp một tại một điểm, cấp hai tại một điểm và cấp một với bốn phương án cho trước.

Riêng với dòng fx 880 BTG thì các bạn có thể sử dụng bảng tính Spreadsheet để tính đạo hàm cấp hai tại một điểm.

Mặc dù việc sử dụng bảng tính Spreadsheet khó hơn một chút nhưng nó cũng có một số ưu điểm nhất định.

Dễ thấy nhất có thể tính được đạo hàm cấp hai tại một điểm khác (cùng hàm số) và tại một điểm khác (khác hàm số) một cách nhanh chóng.

Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo.

Đọc thêm:

• Cách tính đạo hàm cấp hai và cấp cao của một hàm số
• Cách tính đạo hàm cấp 2 bằng máy tính Casio 580 và 880
• Tổng hợp công thức tính đạo hàm của các hàm số thường gặp

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn