4 cách chứng minh hai tam giác vuông bằng nhau (có ví dụ)

Ở bài viết này chúng ta sẽ cùng nhau tìm hiểu về bốn trường hợp bằng nhau trong hai tam giác vuông.

Tất nhiên bạn có thể vận dụng kiến thức cũ trong bài viết (3 cách chứng minh hai tam giác bằng nhau) để chứng minh hai tam giác vuông bằng nhau.

Tuy nhiên, đó không phải là phương án tối ưu nhất, tam giác vuông là tam giác đặc biệt nên sẽ có các cách đặc biệt để chứng minh.

Việc vận dụng tốt 4 cách chứng minh 2 tam giác vuông bằng nhau này sẽ là phương pháp hoàn hảo nhất, giúp bạn tiết kiệm được khá nhiều công sức và thời gian khi làm bài tập.

Trường hợp #1. Hai cạnh góc vuông bằng nhau

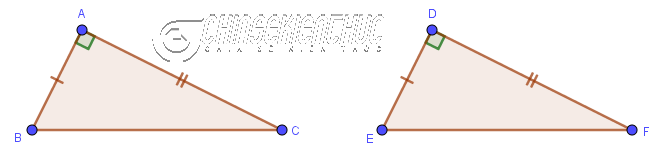
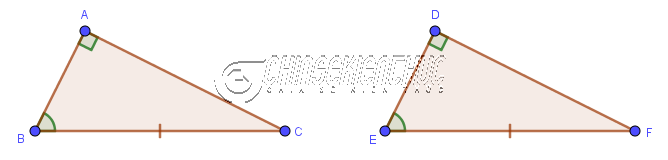
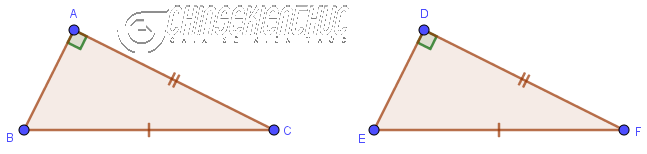
Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng 2 cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đã cho bằng nhau.

$\left.\begin{array}{} AB=DE \\ AC=DF\end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Dễ thấy trường hợp này tương ứng với trường hợp Cạnh Góc Cạnh

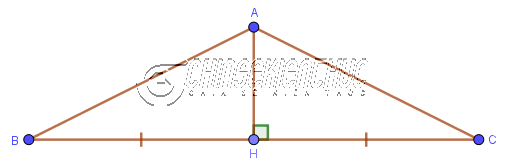
Ví dụ 1: Cho tam giác ABC có AH là đường cao và H là trung điểm của cạnh BC. Chứng minh tam giác ABH bằng tam giác ACH

Xét tam giác ABH và tam giác ACH

• $\widehat{AHB}=\widehat{AHC}=90^o$
• AH là cạnh chung của hai tam giác
• BH=CH (H là trung điểm của cạnh BC)

=> Vậy tam giác ABH bằng tam giác ACH

Trường hợp #2. Một cạnh góc vuông và một góc nhọn bằng nhau

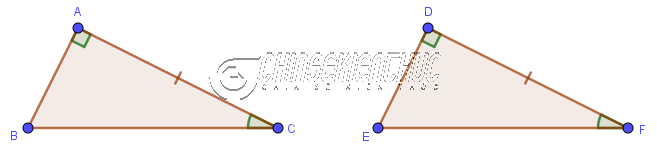
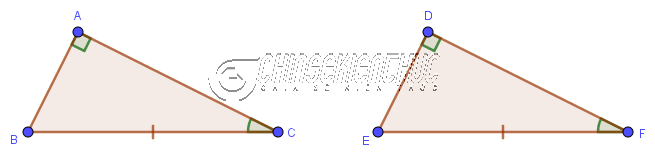
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này lần lượt bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đã cho bằng nhau.

$\left.\begin{array}{} AC=DF \\ \hat{C}=\hat{F} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Trường hợp này tương ứng với trường hợp Góc Cạnh Góc

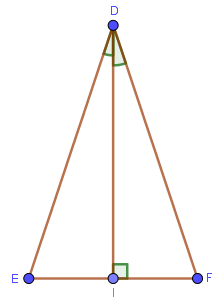
Ví dụ 2: Cho tam giác DEF có DI là đường cao cũng là đường phân giác. Chứng minh tam giác DEI bằng tam giác DFI.

Xét tam giác DEI và tam giác DFI

• $\widehat{DIE}=\widehat{DIF}=90^o$
• DI là cạnh chung của hai tam giác
• $\widehat{EDI}=\widehat{FDI}$ (DI là tia phân giác của $\widehat{EDF}$)

=> Vậy tam giác DEI bằng tam giác DFI

Trường hợp #3. Cạnh huyền và một góc nhọn bằng nhau

Nếu cạnh huyền và một góc nhọn của tam giác vuông này lần lượt bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác đã cho bằng nhau.

$\left.\begin{array}{} BC=EF \\ \hat{B}=\hat{E} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Hoặc:

$\left.\begin{array}{} BC=EF \\ \hat{C}=\hat{F} \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

Thật vậy …

• Tổng ba góc trong một tam giác luôn bằng 180 độ
• Hai góc của hai tam giác tương ứng bằng nhau

=> Suy ra góc còn lại cũng bằng nhau

Vậy trường hợp này tương ứng với trường hợp Góc Cạnh Góc

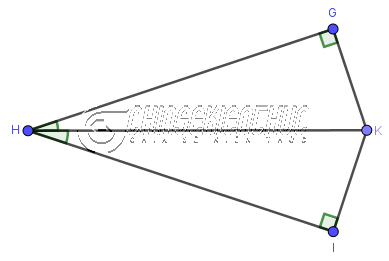
Ví dụ 3: Cho tứ giác GHIK có $\hat{G}=\hat{I}=90^o$ và HK là tia phân giác của $\hat{H}$. Chứng minh tam giác GHK bằng với tam giác IHK.

Xét tam giác vuông GHK và tam giác vuông IHK

• HK là cạnh chung
• $\widehat{GHK}=\widehat{IHK}$ (HK là tia phân giác của $\hat{H}$ )

=> Vậy tam giác GHK bằng tam giác IHK

Trường hợp #4. Cạnh huyền và một cạnh góc vuông bằng nhau

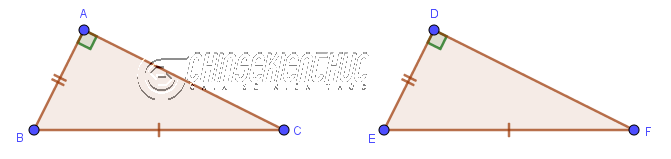
Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này lần lượt bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác đã cho bằng nhau.

$\left.\begin{array}{} BC=EF \\ AB=DE \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Hoặc:

$\left.\begin{array}{} BC=EF \\ AC=DF \end{array}\right\} \Rightarrow \triangle ABC = \triangle DEF$

Thật vậy …

• Trong một tam giác vuông luôn có bình phương độ dài của cạnh huyền bằng tổng bình phương độ dài của hai cạnh góc vuông
• Hai tam giác vuông đã cho có một cạnh huyền và một cạnh góc vuông bằng nhau

Suy ra cạnh góc vuông còn lại chắc chắn cũng bằng nhau

=> Vậy trường hợp này tương ứng với trường hợp Cạnh Cạnh Cạnh

Lời kết

Đến đây chúng ta đã cùng nhau tìm hiểu xong 4 cách để chứng minh 2 tam giác vuông bằng nhau một cách khá chi tiết và đầy đủ rồi.

Chúng ta cũng đã áp dụng định lý tổng ba góc trong một tam giác và định lý Pytago để chứng minh cho Trường hợp 3 và Trường hợp 4. Riêng Trường hợp 4 thì bạn có thể xem nó là một hệ quả của định lý Pytago.

Hi vọng bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com