Định nghĩa và định lý của tứ giác nội tiếp đường tròn

Qua bài viết này các bạn sẽ hiểu rõ hơn về định nghĩa tứ giác nội tiếp đường tròn, biết được mối quan hệ giữa các góc, biết được điều kiện để tứ giác nội tiếp đường tròn, …, xa hơn nữa là chứng minh được tứ giác đã cho là tứ giác nội tiếp đường tròn.

Ngoài ra các bạn còn chỉ ra được trong những tứ giác đặc biệt (hình thang, hình thang cân, hình thang vuông, hình bình hành, hình chữ nhật, hình thoi, hình vuông) tứ giác nào nội tiếp được, tứ giác nào thì không.

Okay, ngay bây giờ chúng ta sẽ đi vào phần chi tiết của bài viết nhé !

#1. Tứ giác nội tiếp đường tròn là gì?

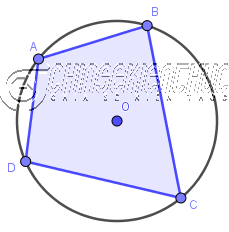
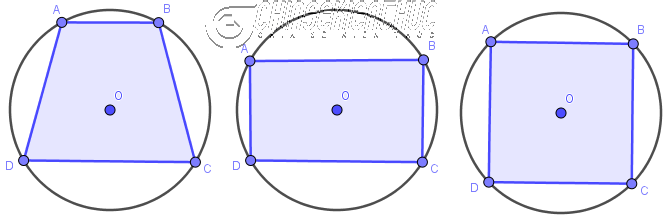
Tứ giác có bốn đỉnh thuộc đường tròn (hay nói cách khác là có 4 đỉnh nằm trên đường tròn) thì được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

Như hình bên trên: Tứ giác ABCD có bốn đỉnh A, B, C, D nằm trên đường tròn tâm O => nên tứ giác nội tiếp đường tròn (hay đường tròn ngoại tiếp tứ giác, các bạn gọi như thế nào cũng được).

Lúc bấy giờ ta nói $\hat{A}$ đối với $\hat{C}$, $\hat{B}$ đối với $\hat{D}$

#2. Định lý thuận của tứ giác nội tiếp

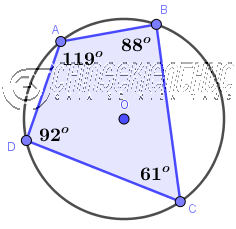
Trong một tứ giác nội tiếp, tổng số đo của hai góc đối diện luôn bằng 180⁰

Tứ giác ABCD nội tiếp đường tròn tâm O nên  $\hat{A}+\hat{C}=119^o+61^o=180^o$ và $\hat{B}+\hat{D}=88^o+92^o=180^o$

#3. Định lý đảo của tứ giác nội tiếp

Nếu một tứ giác có tổng các góc đối bằng 180⁰ thì tứ giác đó nội tiếp được trong đường tròn.

#4. Bài tập ví dụ về tứ giác nội tiếp đường tròn

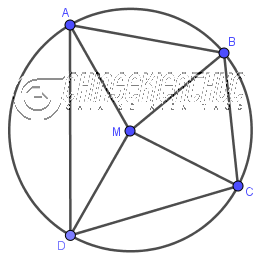
Ví dụ 1: Cho tứ giác ABCD nội tiếp đường tròn tâm M, biết $\widehat{DAB}=80^o$, $\widehat{DAM}=30^o$, $\widehat{BMC}=70^o$

Tính số đo $\widehat{BCM}$, $\widehat{AMB}$

Lời Giải:

Số đo $\widehat{BCM}$

Vì MB = MC (bán kính đường tròn tâm M) nên tam giác BMC là tam giác cân (cân tại M)

Suy ra $\widehat{BCM}=\frac{180^o-70^o}{2}=55^o$

Số đo $\widehat{AMB}$

Dễ thấy $\widehat{MAB}=\widehat{DAB}-\widehat{DAM}=80^o-30^o=50^o$

Vì MA = MB (bán kính đường tròn tâm M) nên tam giác AMB là tam giác cân (cân tại M)

Suy ra $\widehat{AMB}=180^o-2 \times 50^o=80^o$

Vậy số đo $\widehat{BCM}=55^o$, $\widehat{AMB}=80^o$

Casio FX 580 VNX [Mua trên Shopee] [Mua trên Tiki]	CASIO FX 880 BTG [Mua trên Shopee] [Mua trên Lazada]

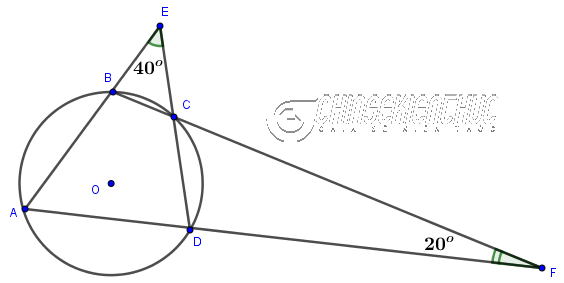
Ví dụ 2: Cho tứ giác ABCD nội tiếp trong đường tròn tâm O, AB cắt DC tại E, BC cắt AD tại F, $\hat{E}=40^o, \hat{F}=20^o$

Tìm số đo $\hat{A}, \hat{B}, \hat{C}, \hat{D}$

Lời Giải:

Dễ thấy $\widehat{BCE}=\widehat{DCF}$ (đối đỉnh)

Chúng ta đặt $x=\widehat{BCE}=\widehat{DCF}$

Theo tính chất góc ngoài của tam giác chúng ta có $\widehat{ABC}=x+40^o$ (1) , $\widehat{ADC}=x+20^o$ (2)

Mặc khác chúng ta lại có $\widehat{ABC}+\widehat{ADC}=180^o$ (3) (Định lí thuận)

Từ ⁽¹⁾, ⁽²⁾ và ⁽³⁾ chúng ta suy ra $(x+40^o)+(x+20^o)=180^o \Leftrightarrow 2x+60^o=180^o \Leftrightarrow x=60^o$

• $\widehat{ABC}=60^o+40^o=100^o$
• $\widehat{ADC}=60^o+20^o=80^o$
• $\widehat{BCD}=180^o-x$ suy ra $\widehat{BCD}=180^o-60^o=120^o$ (hai góc kề bù)
• $\widehat{BAD}=180^o-\widehat{BCD}=180^o-120^o=60^o$ (Định lí thuận)

Vậy số đo $\hat{A}=60^o, \hat{B}=100^o, \hat{C}=120^o, \hat{D}=80^o$

Ví dụ 3: Hình thang cân, hình chữ nhật và hình vuông là các tứ giác nội tiếp, bạn hãy giải thích kết luận trên.

Lời Giải:

Hình thang cân

Dễ thấy $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360^o$ (áp dụng định lý tổng bốn góc trong một tứ giác)

Mặc khác $\hat{A}=\hat{B}$ và $\hat{C}=\hat{D}$

• Suy ra $2\hat{A}+2\hat{C}=360^o \Leftrightarrow \hat{A}+\hat{C}=180^o$
• Suy ra $2\hat{B}+2\hat{D}=360^o \Leftrightarrow \hat{B}+\hat{D}=180^o$

Hình thang cân ABCD có $\hat{A}+\hat{C}=180^o$ và $\hat{B}+\hat{D}=180^o$ nên hình thang cân nội tiếp được đường tròn

Hình chữ nhật và hình vuông

Vì hình chữ nhật và hình vuông là những tứ giác có bốn góc bằng nhau và bằng 90⁰ nên hình chữ nhật và hình vuông nội tiếp được đường tròn.

#5. Lời kết

Vâng, như vậy là qua bài viết này thì mình tin là bạn đã hiểu được rõ ràng hơn về tứ giác nội tiếp đường tròn rồi đúng không?!

Tứ giác nội tiếp đường tròn là một trong những mạch kiến thức rất quan trọng trong chương trình Toán Trung học.

Các bài toán có liên quan đến kiến thức này rất thường gặp trong các kỳ thi tuyển sinh vào lớp 10 hoặc kỳ thi học sinh giỏi.

Vậy nên bạn hãy giành sự quan tâm đặc biệt đến định nghĩa và định lý của tứ giác nội tiếp đường tròn nếu muốn có được kết quả tốt trong các kỳ thi trên nhé.

Bài viết này tuy chỉ cung cấp những kiến thức rất cơ bản về tứ giác nội tiếp nhưng đây sẽ là tiền đề để bạn tiếp cận được những kiến thức chuyên sâu hơn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

Đọc thêm:

• Công thức tính DIỆN TÍCH TỨ GIÁC và CHU VI TỨ GIÁC
• 4 cách chứng minh hai tam giác vuông bằng nhau (có ví dụ)

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com