Cách khảo sát hàm số bậc ba và hàm trùng phương

Hôm nay, mình sẽ hướng dẫn các bạn cách khảo sát sự biến thiên của hàm số bậc ba và hàm số trùng phương.

Việc khảo sát sự biến thiên của hàm số bậc ba và hàm số trùng phương bản chất giống như việc kiểm tra lại kiến thức cũ.

Hay nói cách khác, muốn khảo sát được sự biến thiên của hàm bậc ba và trùng phương thì các bạn cần phải nằm lòng các kiến thức mình vừa liệt kê bên trên.

I. Các bước khảo sát sự biến thiên của hàm số đa thức

Các hàm số bậc ba và hàm số trùng phương được gọi chung là các hàm số đa thức

Bước 1. Tìm tập xác định của hàm số

Vì các hàm số mà chúng ta xét trong bài viết này là các hàm đa thức nên tập xác định là $\mathbb{R}$

Bước 2. Xét sự biến thiên của hàm số

Bước 2.1. Tìm giới hạn tại vô cực

Bước 2.2. Lập bảng biến thiên của hàm số

Để lập được bảng biến thiên của hàm số chúng ta cần:

• Tìm đạo hàm của hàm số
• Xét dấu đạo hàm
• Xét chiều biến thiên và tìm cực trị của hàm số
• Điền các kết quả vào bảng

Bước 3. Vẽ đồ thi của hàm số

• Xác định một số điểm đặc biệt của đồ thị
• Tìm giao điểm của đồ thị với các trục tọa độ

Bước 3.1. Nhận xét về đồ thị

• Chỉ ra trục đối xứng của đồ thị
• Chỉ ta tâm đối xứng của đồ thị

II. Cách khảo sát sự biến thiên của hàm số đa thức

Khảo sát sự biến thiên của hàm số bậc ba $y=ax^3+bx^2+cx+d$ và hàm số trùng phương $y=ax^4+bx^2+c$

#1. Cách khảo sát hàm số bậc 3

Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=\frac{1}{16}\left(x^3-3 x^2-9 x-5\right)$

Lời giải:

Vì hàm số đã cho là hàm đa thức nên có tập xác định là $\mathbb{R}$

+) Sự biến thiên của hàm số

• Giới hạn của hàm số tại vô cực

$\lim _{x \rightarrow-\infty} \frac{1}{16}\left(x^3-3 x^2-9 x-5\right)=-\infty$

$\lim _{x \rightarrow+\infty} \frac{1}{16}\left(x^3-3 x^2-9 x-5\right)=+\infty$

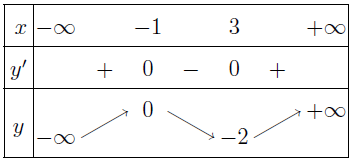
• Bảng biến thiên

$y^{\prime}=\frac{3}{16}\left(x^2-2x-3\right)$

Cho $y’=0$ chúng ta được phương trình $\frac{3}{16}\left(x^2-2x-3\right)=0$

Giải phương trình $\frac{3}{16}\left(x^2-2x-3\right)=0$ chúng ta được các nghiệm là $x=-1$ hoặc $x=3$

Dựa vào bảng biến thiên vừa lập chúng ta nhận thấy:

• Hàm số đồng biến trên khoảng $(-\infty ;-1)$ và $(3 ;+\infty)$
• Nghịch biến trên khoảng $(-1 ; 3)$
• Hàm số đạt cực đại tại điểm $x=-1$ và giá trị cực đại của hàm số là $y(-1)=0$
• Hàm số đạt cực tiểu tại điểm $x=3$ và giá trị cực tiểu của hàm số là $y(3)=-2$

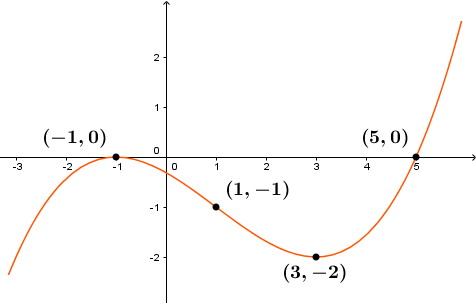
+) Đồ thị hàm số

Dễ thấy, giao điểm của đồ thị với trục tung là điểm $\left(0 ;-\frac{5}{16}\right)$

Cho $y=0$ chúng ta được phương trình $\frac{1}{16}\left(x^3-3 x^2-9 x-5\right)=0$

Giải phương trình $\frac{1}{16}\left(x^3-3 x^2-9 x-5\right)=0$ chúng ta được các nghiệm $x=-1$ hoặc $x=5$

=> Đồ thị và trục hoành có hai điểm chung là $(-1 ; 0)$ và $(5 ; 0)$

$y^{\prime \prime}=\frac{3}{8}(x-1)$

Cho $y^{\prime \prime}=0$ chúng ta được phương trình $\frac{3}{8}(x-1)=0$

Giải phương trình $\frac{3}{8}(x-1)=0$ chúng ta được nghiệm $x=1$

Bảng xét dấu $y^{\prime \prime}=\frac{3}{8}(x-1)$

Vì $y”$ đổi dấu khi $x=1$ nên $U=(1 ;-1)$ là điểm uốn của hàm số đã cho

#2. Cách khảo sát hàm trùng phương

Ví dụ 2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y=2x^4-4x^2-6$

Lời giải:

Vì hàm số đã cho là hàm trùng phương nên tập xác định là $\mathbb{R}$

+) Sự biến thiên của hàm số

• Giới hạn của hàm số tại vô cực

$\lim _{x \rightarrow-\infty} (2x^4-4x^2-6)=+\infty$ và $\lim _{x \rightarrow+\infty} (2x^4-4x^2-6)=+\infty$

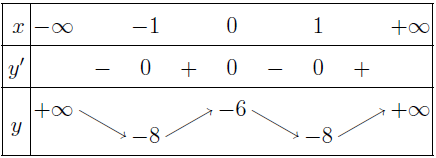
• Bảng biến thiên

$y^{\prime}=8x^3-8x$

Cho $y^{\prime}=0$ chúng ta được phương trình $8x^3-8x=0$

Giải phương trình $8x^3-8x=0$ chúng ta được các nghiệm là $x=0$ hoặc $x=1$ hoặc $x=-1$

Dựa vào bảng biến thiên chúng ta dễ dàng nhận thấy:

• Hàm số nghịch biến trên khoảng $(-\infty ;-1)$ và $(0 ; 1)$
• Đồng biến trên mỗi khoảng $(-1 ; 0)$ và $(1 ;+\infty)$
• Hàm số đạt cực đại tại điểm $x=0$ và giá trị cực đại của hàm số là $y(0)=-6$
• Hàm số đạt cực tiểu tại các điểm $x=1$, $x=-1$ và giá trị cực tiểu của hàm số tại các điểm $x=1$, $x=-1$ lần lượt là $y(1)=-8$, $y(-1)=-8$

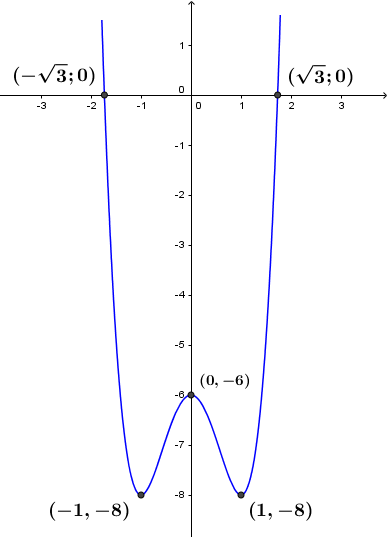
+) Đồ thị hàm số

Dễ thấy giao điểm của đồ thị với trục tung là điểm $(0 ;-6)$

Cho $y=0$ chúng ta được phương trình $2x^4-4x^2-6=0$

Giải phương trình $2x^4-4x^2-6=0$ chúng ta được nghiệm là $x=\sqrt{3}$, $x=-\sqrt{3}$

=> Đồ thị cắt trục hoành tại hai điểm $(\sqrt{3} ; 0)$ và $(-\sqrt{3} ; 0)$

$y^{\prime \prime}=24x^2-8$

Cho $y^{\prime \prime}=0$ chúng ta thu được phương trình $24x^2-8=0$

Giải phương trình $24x^2-8=0$ chúng ta được các nghiệm $x_1=\frac{\sqrt{3}}{3}, x_2=-\frac{\sqrt{3}}{3}$

Bảng xét dấu $y^{\prime \prime}=24x^2-8$

Vì $y”$ đổi dấu khi $x$ qua mỗi điểm $x_1$ và $x_2$ nên $U_1\left(-\frac{\sqrt{3}}{3} ;-\frac{64}{9}\right)$ và $U_2\left(\frac{\sqrt{3}}{3} ;-\frac{64}{9}\right)$ là hai điểm uốn của hàm số

Ngoài ra hàm số đã cho là hàm số chẵn nên đồ thị của nó nhận trục tung làm trục đối xứng

III. Lời kết

Vâng, như vậy là qua bài viết này thì mình tin là bạn đã biết cách khảo sát sự biến thiên của hàm bậc ba và hàm trùng phương rồi đúng không?!

Trước năm 2017 thì việc khảo sát sự biến và vẽ đồ thị của hàm số (bậc ba, trùng phương, phân thức) sẽ là câu đầu tiên trong Kỳ thi Tốt nghiệp THPT và Kỳ thi Tuyển sinh vào Đại học

Nhưng kể từ nằm 2017 trở về sau này thì Bộ Giáo dục và Đào tạo đã thay đổi hình thức thi từ tự luận sang trắc nghiệm.

Tuy vậy, giá trị từ việc khảo sát sự biến của hàm số vẫn không hề thay đổi, bởi sau khi khảo sát xong bạn có thể dễ dàng xác định được:

• Tính đơn điệu (đồng biến, nghịch biến)
• Cực trị (cực đại, cực tiểu)
• Điểm uốn

Hi vọng là bài viết này sẽ hữu ích với bạn. Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com
Edit by Kiên Nguyễn